分类目录：《深入理解机器学习》总目录

---

马尔可夫随机场（Markov Random Field，MRF）是典型的马尔可夫网，这是一种著名的无向图模型，图中每个结点表示一个或一组变量，结点之间的边表示两个变量之间的依赖关系。马尔可夫随机场有一组势函数（Potential Functions），亦称“因子”（Factor），这是定义在变量子集上的非负实函数，主要用于定义概率分布函数。

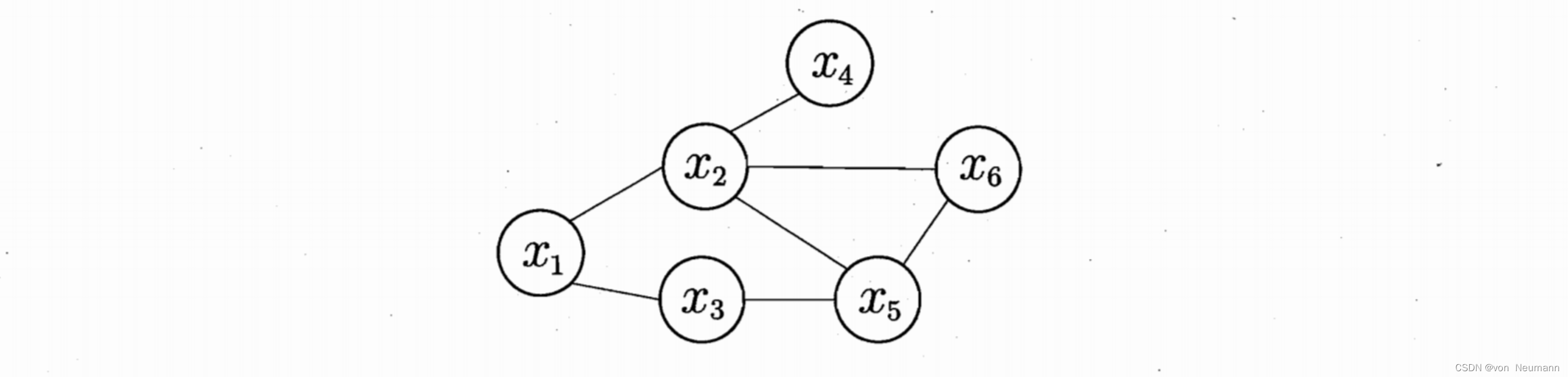
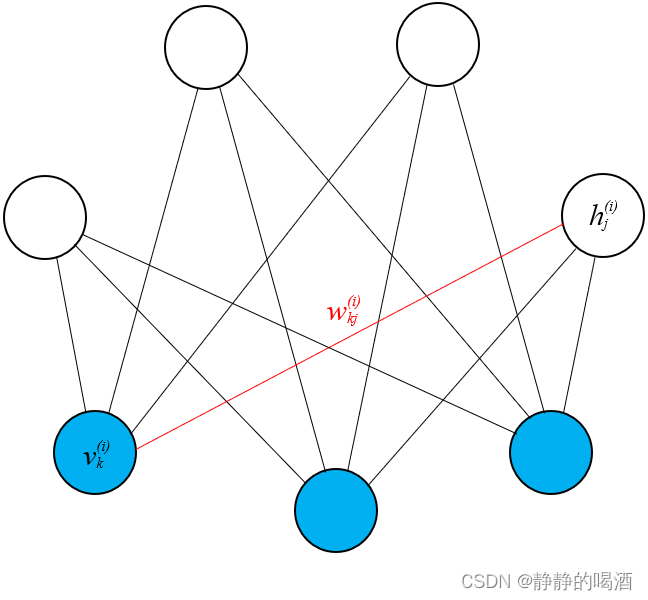
上图显示出一个简单的马尔可夫随机场，对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个“团”（Clique），若在一个团中加入另外任何一个结点都不再形成团，则称该团为“极大团（Maximal Clique）；换言之，极大团就是不能被其他团所包含的团，例如，在上图中 { x 1 , x 2 } \{x_1, x_2\} {x1​,x2​}、 { x 1 , x 3 } \{x_1, x_3\} {x1​,x3​}、 { x 2 , x 4 } \{x_2, x_4\} {x2​,x4​}、 { x 2 , x 5 } \{x_2, x_5\} {x2​,x5​}、 { x 2 , x 6 } \{x_2, x_6\} {x2​,x6​}、 { x 3 , x 5 } \{x_3, x_5\} {x3​,x5​}、 { x 5 , x 6 } \{x_5, x_6\} {x5​,x6​}和 { x 2 , x 5 , x 6 } \{x_2, x_5, x_6\} {x2​,x5​,x6​}都是团，并且除了 { x 2 , x 5 } \{x_2, x_5\} {x2​,x5​}、 { x 2 , x 6 } \{x_2, x_6\} {x2​,x6​}和 { x 5 , x 6 } \{x_5, x_6\} {x5​,x6​}之外都是极大团；但是，因为$x_2$和$x_3$之间缺乏连接， { x 1 , x 2 , x 3 } \{x_1, x_2, x_3\} {x1​,x2​,x3​}并不构成团，显然，每个结点至少出现在一个极大团中。

在马尔可夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关，具体来说，对于$n$个变量 x = { x 1 , x 2 , ⋯   , x n } x=\{x_1, x_2, \cdots, x_n\} x={x1​,x2​,⋯,xn​}，所有团构成的集合为$\mathcal{C}$，与团$Q\in \mathcal{C}$对应的变量集合记为$x_Q$，则联合概率$P(x)$定义为：
$$P(x)=\frac{1}{Z}\prod _{Q\in \mathcal{C}}{\psi }_Q(x_Q)$$

其中${\psi }_Q$为与团$Q$对应的势函数，用于对团$Q$中的变量关系进行建模，$Z={\sum }_x{\prod }_{Q\in \mathcal{C}}{\psi }_Q(x_Q)$为规范化因子，以确保$P(x)$是被正确定义的概率，在实际应用中，精确计算$Z$通常很困难，但许多任务往往并不需获得$Z$的精确值显然，若变量个数较多，则团的数目将会很多（例如，所有相互连接的两个变量都会构成团），这就意味着上式会有很多乘积项，显然会给计算带来负担。注意到若团$Q$不是极大团，则它必被一个极大团$Q^{\ast }$所包含，即$x_Q\subseteq x_Q^{\ast }$。这意味着变量$x_Q$之间的关系不仅体现在势函数${\psi }_Q$中，还体现在${\psi }_{Q^{\ast }}$中。于是，联合概率$P(x)$可基于极大团来定义。假定所有极大团构成的集合为${\mathcal{C}}^{\ast }$，则有：$$P(x)=\frac{1}{Z^{\ast }}\prod _{Q\in {\mathcal{C}}^{\ast }}{\psi }_Q(x_Q)$$

如上图中 x = { x 1 , x 2 , x 3 , ⋯   , x 6 } x=\{x_1, x_2, x_3, \cdots, x_6\} x={x1​,x2​,x3​,⋯,x6​}，联合概率分布$P(x)$定义为：
$$P(x)=\frac{1}{Z}{\psi }_{12}(x_1,x_2){\psi }_{13}(x_1,x_3){\psi }_{24}(x_2,x_4){\psi }_{35}(x_3,x_5){\psi }_{256}(x_2,x_5,x_6)$$

其中，势函数${\psi }_{256}(x_2,x_5,x_6)$定义在极大团 { x 2 . x 5 , x 6 } \{x_2. x_5, x_6\} {x2​.x5​,x6​}上，由于它的存在，使我们不再需为团 { x 2 , x 5 } \{x_2, x_5\} {x2​,x5​}、 { x 2 , x 6 } \{x_2, x_6\} {x2​,x6​}和 { x 5 , x 6 } \{x_5, x_6\} {x5​,x6​}构建势函数。

在马尔可夫随机场中如何得到“条件独立性”呢？同样借助“分离”的概念，如下图所示，若从结点集$A$中的结点到$B$中的结点都必须经过结点集$C$ 中的结点，则称结点集$A$和$B$被结点集$C$分离，$C$称为“分离集（Separating Set）。对马尔可夫随机场，有全局马尔可夫性（Global Markov Property），即给定两个变量子集的分离集，则这两个变量子集条件独立。如下图，若令$A$、$B$和$C$对应的变量集分别为$x_A$，$x_B$和$x_C$，则$x_A$和$x_B$在给定$x_C$的条件下独立，记为：$x_A\perp x_B|x_C$。

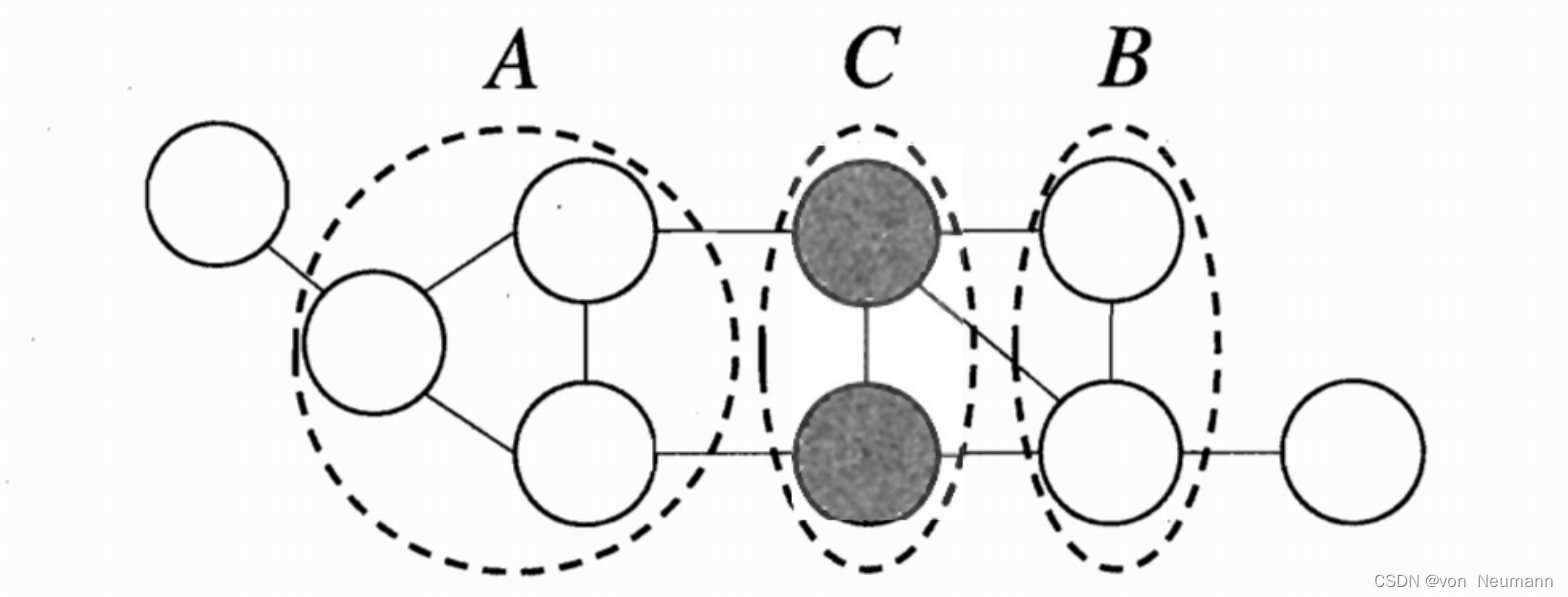
由全局马尔可夫性可得到两个很有用的推论：

• 局部马尔可夫性（Local Markov Property）：给定某变量的邻接变量，则该变量条件独立于其他变量。形式化地说，令$V$为图的结点集，$n(v)$为结点$v$在图上的邻接结点， n ∗ ( v ) = n ( v ) ∪ { v } n^*(v)=n(v)\cup \{v\} n∗(v)=n(v)∪{v}，则有$x_v\perp x_{V\backslash n^{\ast }(v)}|n(v)$
• 成对马尔可夫性（Pairwise Markov Property）：给定所有其他变量，两个非邻接变量条件独立。形式化地说，令图的结点集和边集分别为$V$和$E$，对图中的两个结点$u$和$v$，若$<u,v>\notin E$，则$x{u}_{\perp }{x}_v|x_{V\backslash <u,v>}$

现在我们来考察马尔可夫随机场中的势函数，显然，势函数${\psi }_Q(x_Q)$的作用是定量刻画变量集$x_Q$中变量之间的相关关系，它应该是非负函数，且在所偏好的变量取值上有较大函数值，例如，假定上图的变量均为二值变量，若势函数为：
$$\begin{gathered} {\psi }_{AC}(x_A,x_C)=\{\begin{array}{rl}1.5,& \text{if}{x}_A=x_C\\ 0.1,& \text{otherwise}\end{array} \\ {\psi }_{BC}(x_B,x_C)=\{\begin{array}{rl}0.2,& \text{if}{x}_B=x_C\\ 1.3,& \text{otherwise}\end{array} \end{gathered}$$
则说明该模型偏好变量$x_A$与$x_C$拥有相同的取值，$x_B$与$x_C$拥有不同的取值；换言之，在该模型中$x_A$与$x_C$正相关，$x_B$与$x_C$负相关。所以，令$x_A$与$x_C$相同且$x_B$与$x_C$不同的变量值指派将取得较高的联合概率，为了满足非负性，指数函数常被用于定义势函数，即：
$${\psi }_Q(x_Q)=e^{-H_Q(x_Q)}$$

其中，$H_Q(x_Q)$是一个定义在变量$x_Q$上的实值函数，常见形式为：
$$H_Q(x_Q)=\sum _{u,v\in Q,u\ne v}{\alpha }_{uv}{x}_u{x}_v+\sum _{v\in Q}{\beta }_v{x}_v$$

其中${\alpha }_{uv}$和${\beta }_v$是参数。上式中的第二项仅考虑单结点，第一项则考虑每一对结点的关系。

参考文献：
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.