引言

上一节介绍了含隐变量能量模型的对数似然梯度求解。本节针对受限玻尔兹曼机，对模型参数进行求解。

回顾：含隐变量能量模型的对数似然梯度

已知一个随机变量集合$\mathcal{X}$，随机变量间关系可描述成马尔可夫随机场，并包含观测变量$v$和隐变量$h$两种。
根据能量模型的描述，将联合概率分布$\mathcal{P}(\mathcal{X})$表示为如下形式：
P ( X ) = P ( h , v ) = 1 Z exp ⁡ { − E [ h , v ] } \mathcal P(\mathcal X) = \mathcal P(h,v) = \frac{1}{\mathcal Z} \exp\{ - \mathbb E[h,v]\} P(X)=P(h,v)=Z1​exp{−E[h,v]}
其中，$\mathcal{Z}$表示配分函数。如果此时给定样本集合(基于观测变量的集合)：
V = { v ( i ) } i = 1 N v ( i ) ∈ R n \mathcal V = \{v^{(i)}\}_{i=1}^N \quad v^{(i)} \in \mathbb R^n V={v(i)}i=1N​v(i)∈Rn
关于样本集合$\mathcal{V}$的对数似然$\mathcal{L}(\theta )$可表示为：
各样本间依然服从‘独立同分布’。
$$\mathcal{L}(\theta )=\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)};\theta )$$
对于对数似然$\mathcal{L}(\theta )$的梯度${\nabla }_{\theta }\mathcal{L}(\theta )$可表示为：
$$\begin{array}{rl}{\nabla }_{\theta }\mathcal{L}(\theta )& =\frac{\partial }{\partial \theta }\left[\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)};\theta )\right]\\ & =\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}{\nabla }_{\theta }\log \mathcal{P}(v^{(i)};\theta )\\ {\nabla }_{\theta }\log \mathcal{P}(v^{(i)};\theta )& =\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot \frac{\partial }{\partial \theta }\left[\mathbb{E}(h^{(i)},v^{(i)})\right]\right\}-\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{\partial }{\partial \theta }\left[\mathbb{E}(h^{(i)},v^{(i)})\right]\right\}\\ & \Rightarrow \{\begin{array}{l}{h}^{(i)}=(h_1^{(i)},h_2^{(i)},\cdots ,h_m^{(i)}{)}^T\\ v^{(i)}=(v_1^{(i)},v_2^{(i)},\cdots ,v_n^{(i)}{)}^T\\ m+n=p\end{array}\end{array}$$

受限玻尔兹曼机的对数似然梯度

模型参数求解主体思路

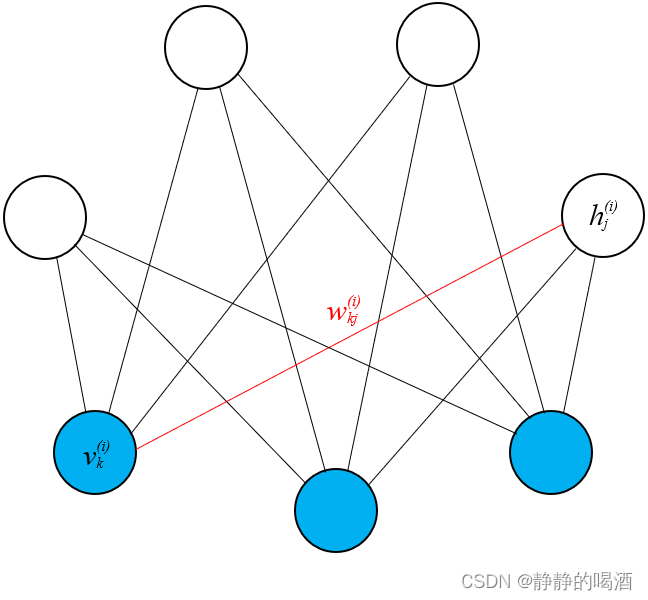
基于受限玻尔兹曼机结构的联合概率分布$\mathcal{P}(\mathcal{X})$表示如下：
$$\mathcal{P}(\mathcal{X})=\mathcal{P}(h,v)=\frac{1}{\mathcal{Z}}\exp \left[v^T\mathcal{W}h+b^{T}v+c^{T}h\right]$$
关于模型参数$\theta$的描述，自然是 θ = { W , b , c } \theta = \{\mathcal W,b,c\} θ={W,b,c}。但本质上只有一种信息表示：结点之间关联关系的表示。其中$b,c$分别表示某观测变量/某隐变量与自身的关联关系，这种关系被视作特殊的节点间关系。在本节中，仅求解一般性的关联关系——存在边的，隐变量与观测变量之间的关联关系，也就是模型参数$\mathcal{W}$：
$$\mathcal{W}={\left(\begin{array}{c}{w}_{11},w_{12},\cdots ,w_{1n}\\ w_{21},w_{22},\cdots ,w_{2n}\\ ⋮\\ w_{m1},w_{m2},\cdots ,w_{mn}\end{array}\right)}_{m\times n}{\mathcal{W}}^{(i)}=[w_{kj}^{(i)}{]}_{m\times n}$$

主体思路：如果能够将$\mathcal{W}$的梯度求解出来，自然就可以使用极大似然估计，基于梯度上升法，将$\mathcal{W}$近似出来：
$${\mathcal{W}}^{(t+1)}\Leftarrow {\mathcal{W}}^{(t)}+\eta {\nabla }_{\mathcal{W}}\mathcal{L}(\mathcal{W})$$

求解过程

基于能量模型的对数似然梯度，将受限玻尔兹曼机的结构表示代入公式中：
依然仅针对一个观测样本$v^{(i)}$,该样本的第$k$个分量(维度)$v_k^{(i)}$和对应隐变量$h^{(i)}$的第$j$个分量$h_j^{(i)}$之间的模型参数$w_{kj}^{(i)}$进行积分。

$$\begin{array}{rl}{\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]& =\frac{\partial }{\partial w_{kj}^{(i)}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\\ & =-\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{\partial }{\partial w_{kj}^{(i)}}\left[\mathbb{E}[h^{(i)},v^{(i)}]\right]\right\}+\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot \frac{\partial }{\partial w_{kj}^{(i)}}\left[\mathbb{E}(h^{(i)},v^{(i)})\right]\right\}\end{array}$$
由于这里不考虑模型参数$b,c$的影响，使用$\Delta$进行表示。因而 能量函数$\mathbb{E}[h^{(i)},v^{(i)}]$可表示为如下形式：
$$\begin{array}{rl}\mathbb{E}[h^{(i)},v^{(i)}]& =-\left\{[h^{(i)}{]}^T{\mathcal{W}}^{(i)}{v}^{(i)}+{\Delta }^{(i)}\right\}\\ & =-\left(\sum _{k=1}^m\sum _{j=1}^n{h}_k^{(i)}\cdot w_{kj}^{(i)}\cdot v_j^{(i)}+{\Delta }^{(i)}\right)\end{array}$$
将其代入，有：
能量函数$\mathbb{E}[h^{(i)},v^{(i)}]$仅对$w_{kj}^{(i)}$一项进行求导，连加号${\sum }_{\ne k}^m,{\sum }_{\ne j}^n$均视作常数:
$$\begin{array}{rl}\frac{\partial }{\partial w_{kj}^{(i)}}\left[\mathbb{E}[h^{(i)},v^{(i)}]\right]& =\frac{\partial }{\partial w_{kj}^{(i)}}\left[-\left(h_1^{(i)}\cdot w_{11}^{(i)}\cdot v_1^{(i)}+\cdots h_k^{(i)}\cdot w_{kj}^{(i)}\cdot v_j^{(i)}+\cdots +h_m^{(i)}\cdot w_{mn}^{(i)}\cdot v_n^{(i)}+{\Delta }^{(i)}\right)\right]\\ & =\frac{\partial }{\partial w_{kj}^{(i)}}\left[-\left(h_k^{(i)}\cdot w_{kj}^{(i)}\cdot v_j^{(i)}\right)\right]\\ & =-h_k^{(i)}{v}_j^{(i)}\\ {\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]& =-\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot (-h_k^{(i)}{v}_j^{(i)})\right\}+\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot (-h_k^{(i)}{v}_j^{(i)})\right\}\end{array}$$
继续化简，有：
$$\begin{array}{rl}{\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]& =\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}-\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}\end{array}$$
这里依然假设变量信息(隐变量、观测变量)服从伯努利分布(Bernoulli Distribution)，因而所有变量均是离散型随机变量，并且仅有两种取值：$0,1$。基于这种假设，可以继续向下化简：

• 先观察等号右侧第一项：
  将${\sum }_{h^{(i)}}$按照随机变量维度展开.
除去${\sum }_{h_k^{(i)}}$项之外的其他项全被积分掉了。例如：
  $$\begin{array}{rl}& \sum _{h_1^{(i)}}\mathcal{P}(h_1^{(i)},h_2^{(i)},\cdots ,h_m^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\\ & =h_k^{(i)}{v}_j^{(i)}\cdot \sum _{h_1^{(i)}}\mathcal{P}(h_1^{(i)},h_2^{(i)},\cdots ,h_m^{(i)}\mid v^{(i)})\\ & =h_k^{(i)}{v}_j^{(i)}\cdot \mathcal{P}(h_2^{(i)},\cdots ,h_m^{(i)}\mid v^{(i)})\end{array}$$
  剩余的项以此类推~从而有：
  $$\begin{array}{rl}\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}& =\sum _{h_1^{(i)}},\cdots ,\sum _{h_k^{(i)}},\cdots ,\sum _{h_m^{(i)}}\left\{\mathcal{P}(h_1^{(i)},\cdots ,h_k^{(i)},\cdots ,h_m^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}\\ & =\sum _{h_k^{(i)}}\mathcal{P}(h_k^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\end{array}$$
  将 h k ( i ) = { 0 , 1 } h_k^{(i)} = \{0,1\} hk(i)​={0,1}分别代入，有：
  $$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}+0$$
• 再观察等号右侧第二项：
  将$\mathcal{P}(h^{(i)},v^{(i)})$按照条件概率公式展开.
将仅和$v^{(i)}$相关的和仅和$h^{(i)}$相关的项分开.
第一项的结果${\sum }_{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}=\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}$直接拿来用就可以。
  $$\begin{array}{rl}\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}& =\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}\\ & =\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot h_k^{(i)}{v}_j^{(i)}\right\}\\ & =\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\end{array}$$

最终，受限玻尔兹曼机的梯度可表示为：
$${\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]=\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}-\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}$$

继续观察等号右侧第一项：$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}$由于$v^{(i)}$是一个样本，那么$v_j^{(i)}$自然是已知的；而$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})$在受限玻尔兹曼机——推断任务(后验概率)可以将其表示为Sigmoid函数的形式：
$$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})=\text{Sigmoid}(\sum _{l=1}^n{w}_{lk}^{(i)}\cdot v_l+c_l)$$
因此可以判定：第一项是可求的。

关于等号右侧第二项：${\sum }_{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}$
这里关于$v^{(i)}$的积分是约不掉的，基于它的伯努利分布，v^{(i)}的$n$维随机变量，其时间复杂度是$\mathcal{O}(n)=2^n$。因此不能硬求它的梯度结果。需要使用吉布斯采样/对比散度的方式进行求解。

下一节将继续介绍关于受限玻尔兹曼机使用对比散度的方式求解对数似然梯度。

相关参考：
直面配分函数：6-Log-Likelihood Gradient of RBM