文章目录
- 快速排序
- 递归实现快速排序
- hoare版本
- DigHole版本
- 前后指针版本
- 非递归实现快速排序
- 算法优化
- 1. 针对有序数组进行优化
- 2. 针对全相等数组进行优化
- 算法分析
- 时间复杂度
- 空间复杂度
快速排序
快速排序(英语:Quicksort),又称分区交换排序(partition-exchange sort),是一种排序算法。在平均状况下,排序n个项目要 O ( n l o g n ) O(nlogn) O(nlogn)次比较。最坏的情况下需要 O ( n 2 ) O(n^2) O(n2)次比较,但是最坏的情况并不常见。快速排序通常情况下比其他的排序速度更快。
递归实现快速排序
快速排序是一种分治的思想。在待排序项目中取出一个值作为基准值,将基准值通过一趟排序放入合适的位置,**保证基准值经过一趟排序后的左边所有项目都小于该基准值,右边所有项目都大于该基准值。**在对左边重复上述过程,对右边重复上述过程。
因此快速排序的步骤是
- 挑选基准值:选取待排序项目中某一个数据作为基准值
- 分割:通过合适的方法将基准值放入有序时适当的位置,使得比基准值小的数据放在基准值左边,比基准值大的数据放在基准值右边
- 递归子序列:对基准值左边重复上述1.2.对基准值右边重复上述1.2.
基准值通常选取待排序项目中的第一个项目、最后一个项目或者中间的项目
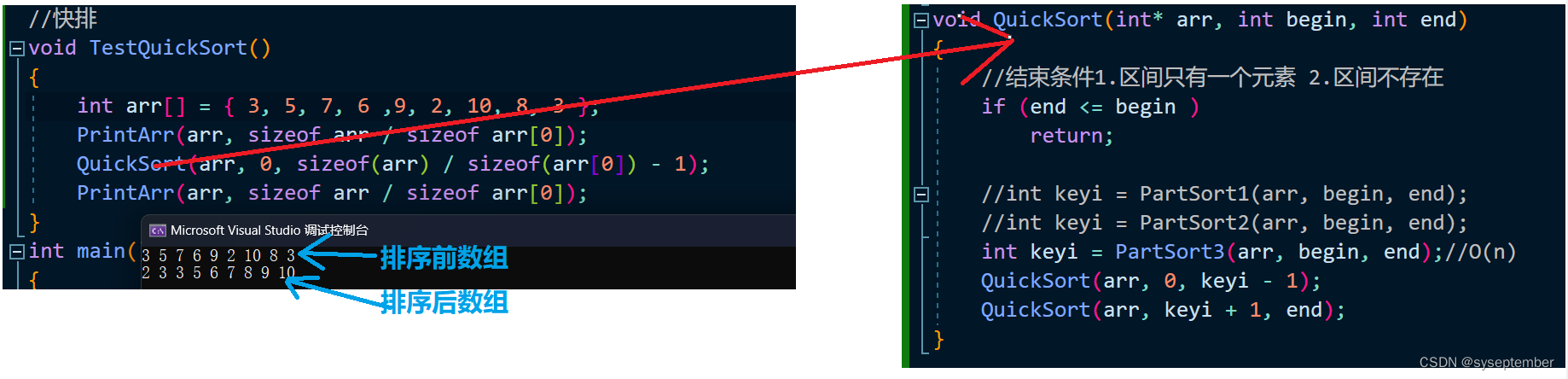
因此我们可以写出快速排序的基本框架
//区间为左闭右闭[begin, end]
void QuickSort(int* arr, int begin, int end)
{
//结束条件1.区间只有一个元素 2.区间不存在
if (end <= begin )
return;
int keyi = PartSort(arr, begin, end);//这一步是分割,保证了基准值在合适的位置,并且返回基准值的位置
QuickSort(arr, 0, keyi - 1);//递归处理基准值左边的部分
QuickSort(arr, keyi + 1, end);//递归处理基准值右边的部分
}
我们下面介绍3种方法完成对基准值的分割。
hoare版本
hoare完成单趟排序基本思路
- 选取第一个待排数据为基准值(key)
- L从begin开始,R从end开始相向运动
- R先向左运动寻找比key小的
- L后向右运动寻找比key大的
- 交换L和R位置的数值
- 重复(3,4)直至L和R相遇
- 交换key和相遇位置的值
注意:若选取第一个待排数据为基准值那么一定要R先动才能保证相遇位置的值比key小,若选取最后一个待排数据为基准值,那么一定要L先动才能保证相遇位置的值比key大。
代码
//hoare法
int PartSort1(int* arr, int begin, int end)
{
//以begin为keyi(keyi是基准值的下标)
int keyi = begin;
int L = begin;
int R = end;
while (L < R)//L和R相遇前
{
//R寻找小于key的
while (L < R && arr[R] >= arr[keyi]) R--;
//L寻找大于key的
while (L < R && arr[L] <= arr[keyi]) L++;
//交换L和R位置的值
Swap(&arr[R], &arr[L]);
}
//交换key与相遇位置的值
Swap(&arr[keyi], &arr[L]);
return L;
}
运行结果
hoare版本的注意点比较多,一不留神容易死循环或者越界
注意
-
L只能从begin开始,不能从begin后面一个位置开始,否则出现下面这种情况
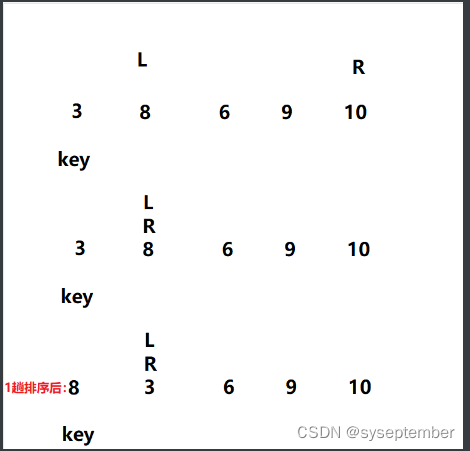
-
R寻找小于key的循环条件是
arr[keyi] <= arr[R] && L < R第一个条件中的等号不可以省略,第二条件不可以省略。
如果第一个条件中的省略号省略了,可能会死循环例如
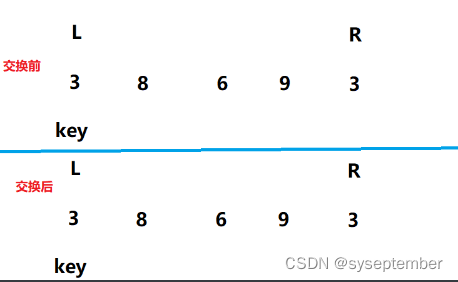
如果第二个条件省略了可能会造成越界例如

hoare版本最后一个需要注意如果我们每次将key值锁定为区间第一个元素,那么我们一定要先移动R,后移动L,这样一定可以保证L与R相遇处的值小于等于key。
**解释:**相遇时只有2种情况,R遇见L和L遇见R
无论L和动还是R先动,相遇前最后的状态一定是这样的
下面是2中R遇见L和L遇见R两种情况:
hoare版本的细节非常的多,一不注意就会踩坑,有人就提出了更不容易写错的版本,挖坑法~
DigHole版本
挖坑法处理单趟排序的主要思路
- 将第一个数据放在key中,形成临时坑位
- R先向左移动直至找到小于key的值,并将该值填入坑中,R所处位置变成新坑
- L向右移动直至找到大于key的值,并将该值填入坑中,L所处的位置变成新坑
- 重复(2.3)直至LR相遇,将key填入相遇位置的坑

代码
//挖坑法
int PartSort2(int* arr, int left, int right)
{
int key = arr[left];//保留首个数据到key中
int hole = left;//第一个坑为第一个数据
int L = left;
int R = right;
while (L < R)//循环条件为LR为相遇
{
//R找小与key的
while (R > L && arr[R] >= key) R--;
arr[hole] = arr[R];//将R位置的值填入坑中
hole = R;//坑变为R所处的位置
//L找大于key的
while (R > L && arr[L] <= key) L++;
arr[hole] = arr[L];//将L位置的值填入坑中
hole = L;//坑变为L所处的位置
}
arr[R] = key;//将key填入相遇处的坑
return R;//返回相遇位置
}
运行结果
hoare版本和DigHole版本都比较繁琐,循环条件稍不留神就会出错,因此有另一种简介的方法完成单趟排序—双指针
前后指针版本
双指针法完成单趟排序基本思路
- 选择待排数据首元素为基准值key
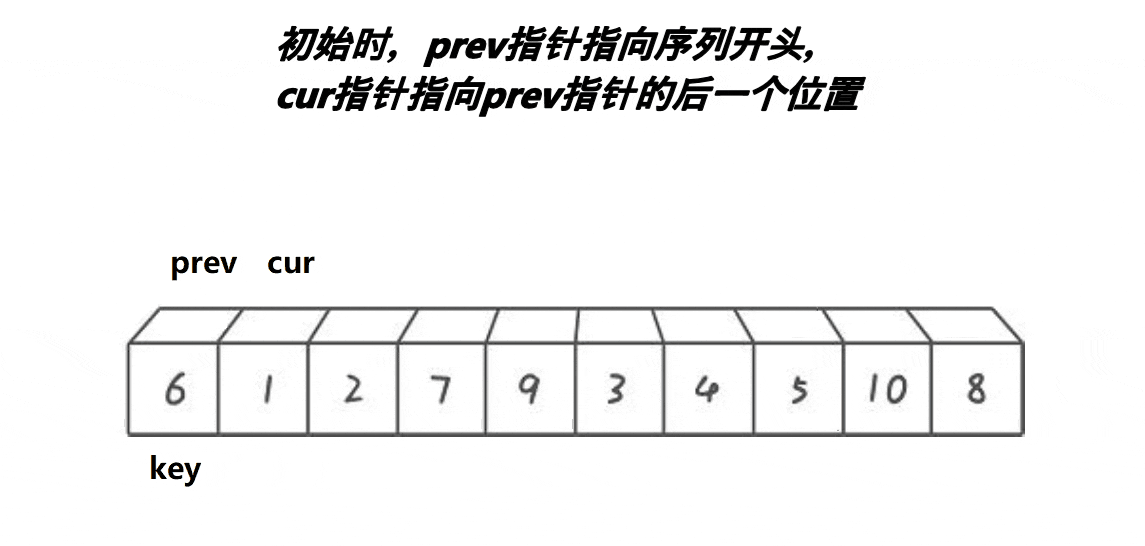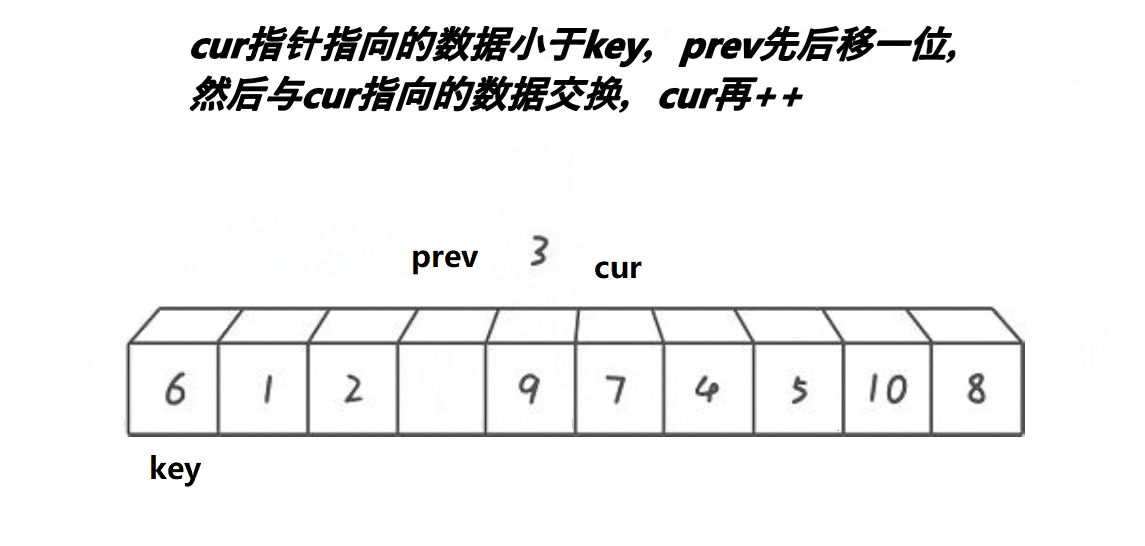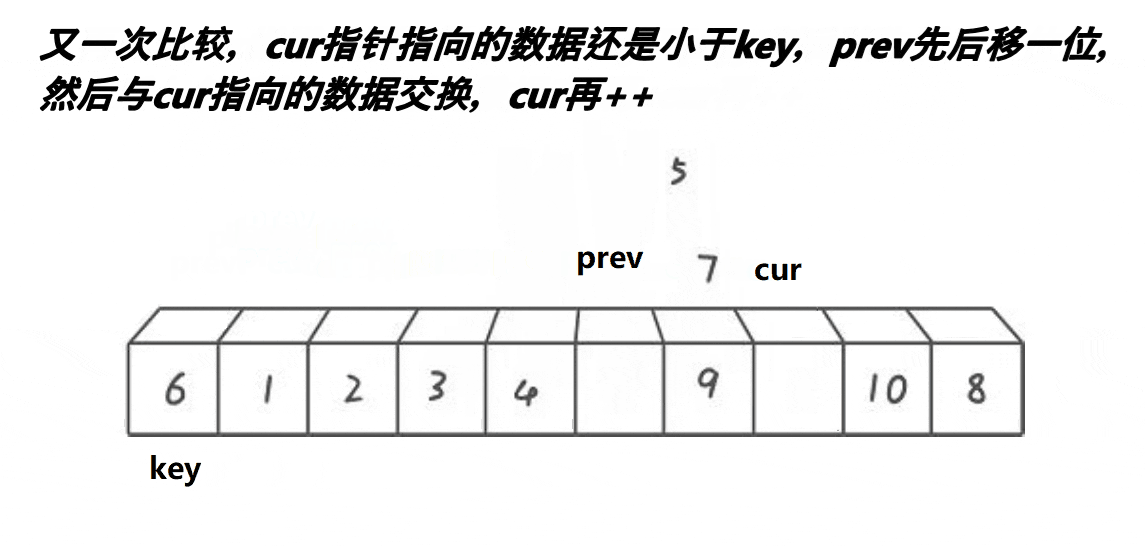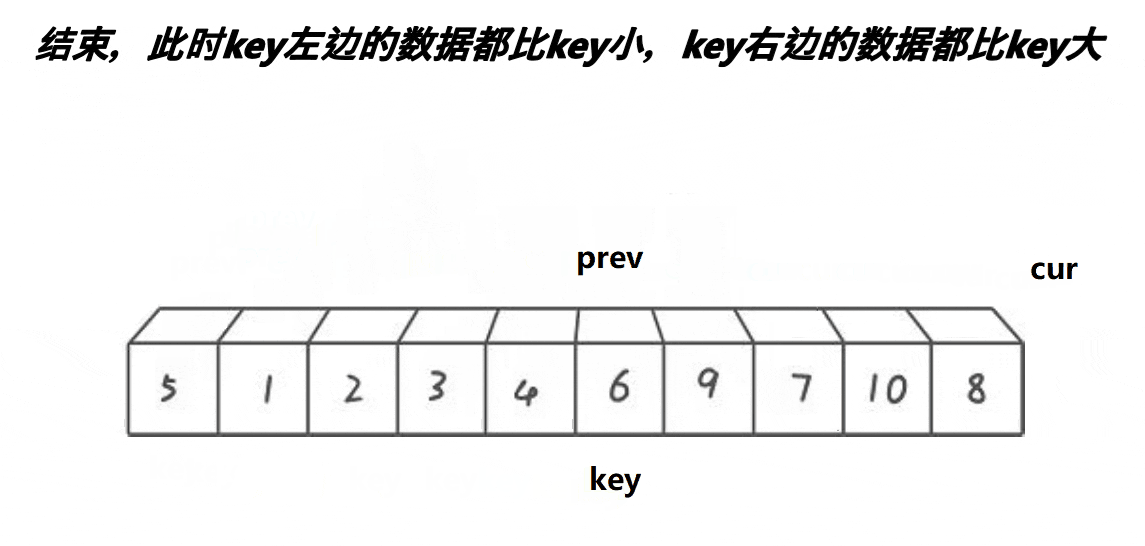
- 定义cur指针指向待排数据的当前元素;pre指针指向cur指针后面一个元素(最开始保证cur与pre相邻)
- 若cur指针指向的值大于key,cur++保证cur和pre之间的元素全部大于基准值
- 若cur指针指向的值不大于key,pre++并且交换pre和cur所指的值
- 重复(3.4)直至cur超过右边界
- 交换pre与keyi所指的值,返回pre
实际上3.4)步保证了大于key的值在最右边,小于key的值在最左边
代码
int PartSort3(int* arr, int left, int right)
{
int prev = left; //prev指向第一个元素
int cur = prev + 1; //cur指向prev后面一个元素
int keyi = left; //key的值选为待排数据第一个元素
while (cur <= right) //循环条件为cur为超过右边界
{
if (arr[cur] < arr[keyi]) //cur指向的值小于prev,prev++并且交换与cur所指向的值
{
Swap(&arr[++prev], &arr[cur]);//交换++prev和cur所指向的值
}
cur++; //cur向后移动一位
}
Swap(&arr[keyi], &arr[prev]); //交换keyi和prev所指向的值
return prev;
}
执行结果
个人认为双指针版本最不容易理解,也是最不容易写错的
非递归实现快速排序
思路:
- 将待排数据最后一个元素下标
end入栈,再将待排数据首元素下标begin入栈 - 先取出栈顶元素为
left,再取出栈顶元素为right - 单趟处理
[left,right]得到keyi - 若
keyi的右区间存在,重复(1),若keyi的左区间存在,重复(1)。若左右区间不存在则不入栈 - 重复(2,3,4)直至栈为空
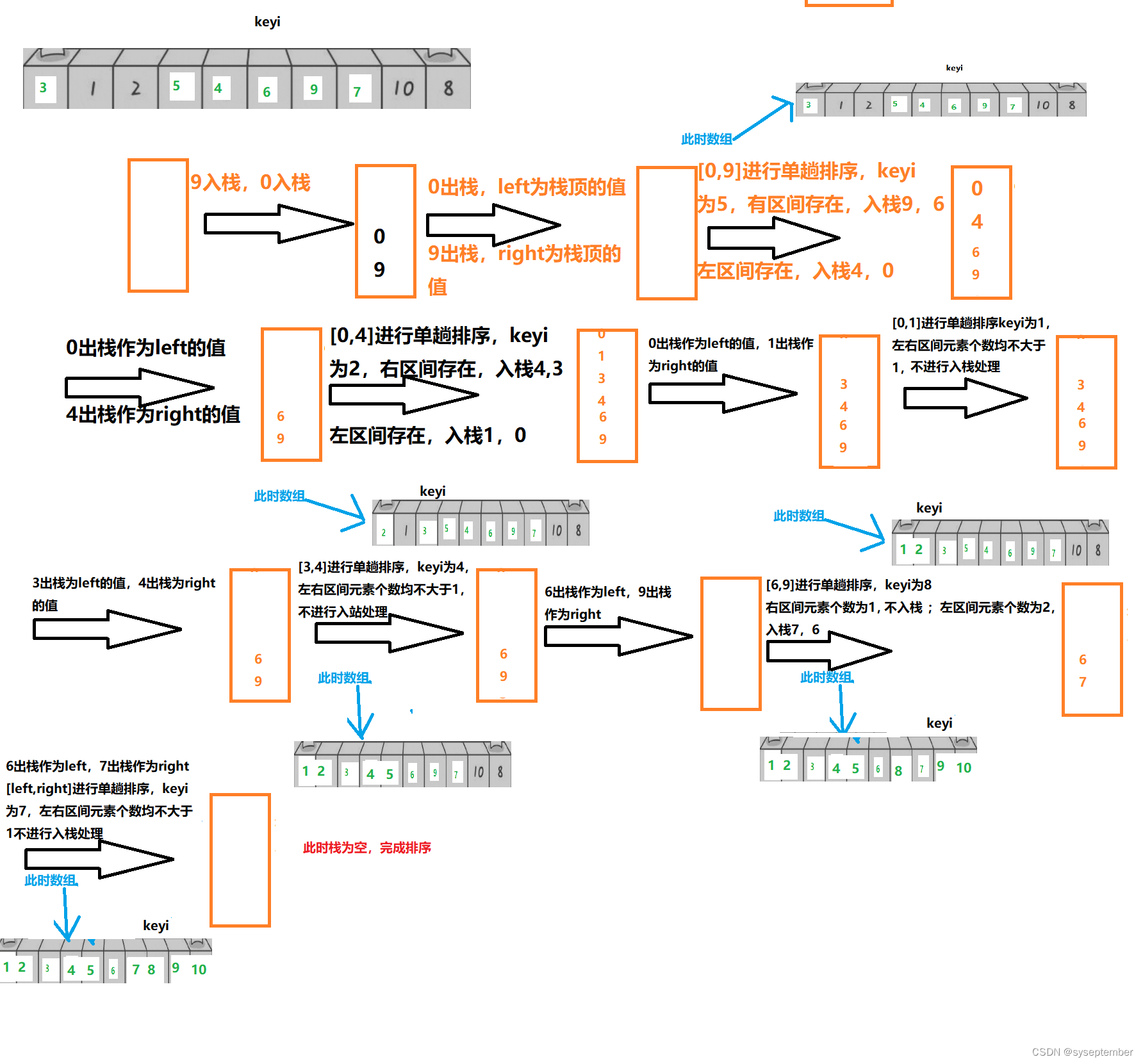
代码
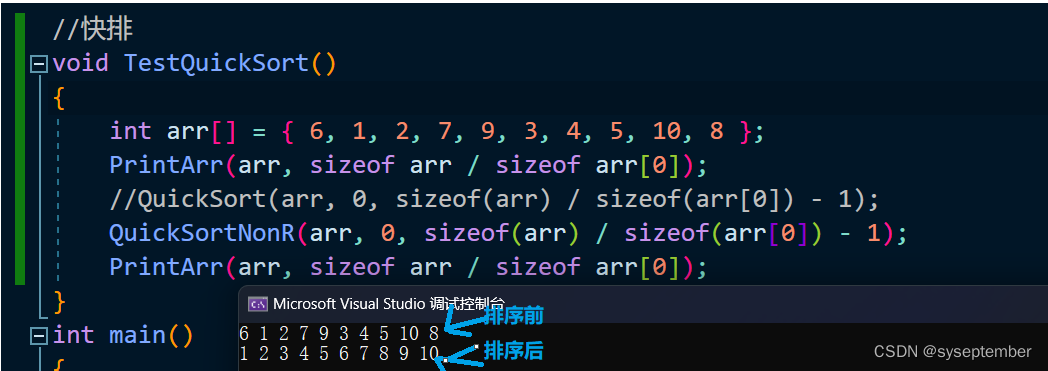
//快排非递归
void QuickSortNonR(int* arr, int begin, int end)
{
Stack st;
StackInit(&st);
StackPush(&st, end);
StackPush(&st, begin);
while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
int keyi = PartSort1(arr, left, right);
//如果右区间个数大于1则入栈
if (keyi + 1 < right)
{
StackPush(&st, end);
StackPush(&st, keyi + 1);
}
//如果左区间个数大于1则入栈
if (keyi - 1 > left)
{
StackPush(&st, keyi - 1);
StackPush(&st, begin);
}
}
StackDestroy(&st);
}
运行结果
算法优化
1. 针对有序数组进行优化
前面说过,当待排数据本身有序时QuickSort的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)(即使这种情况很少见)因此我们可以通过更改基准值实现优化的目的。
三数取中优化:将基准值取为待排数据中首元素、尾元素和中间元素的中间值,这保证了无论元数据是否有序,基准值都不会是最大值或最小值
代码
int GetMidi(int* arr, int begin, int end)
{
int midi = (begin + end) / 2;
if (arr[begin] > arr[end])
{
if (arr[midi] > arr[begin])
return begin;
else if (arr[end] > arr[midi])
return end;
else if (arr[end] < arr[midi])
return midi;
}
else //arr[begin] < arr[end]
{
if (arr[midi] < arr[begin])
return begin;
else if (arr[end] < arr[midi])
return end;
else if (arr[end] > arr[midi])
return midi;
}
}
int PartSort3(int* arr, int left, int right)
{
//保证第一个元素不是最值
int midi = GetMidi(arr, left, right);
Swap(&arr[left], &arr[midi]);
int prev = left; //prev指向第一个元素
int cur = prev + 1; //cur指向prev后面一个元素
int keyi = left; //key的值选为待排数据第一个元素
while (cur <= right) //循环条件为cur为超过右边界
{
if (arr[cur] < arr[keyi]) //cur指向的值小于prev,prev++并且交换与cur所指向的值
{
if (cur != prev + 1); //cur和prev之间有大于key的元素
{
Swap(&arr[++prev], &arr[cur]);//交换++prev和cur所指向的值
}
}
cur++; //cur向后移动一位
}
Swap(&arr[keyi], &arr[prev]); //交换keyi和prev所指向的值
return prev;
}
void QuickSort(int* arr, int begin, int end)
{
//结束条件1.区间只有一个元素 2.区间不存在
if (end <= begin )
return;
int keyi = PartSort3(arr, begin, end);
QuickSort(arr, 0, keyi - 1);
QuickSort(arr, keyi + 1, end);
}
下面是优化后的快排和未优化的快排排100000个随机数效率的差异
**注意:**如果
三数取中仍然过不了可以使用随机数取中,只需要将midi = GetMidi(arr, begin, end)替换成midi = begin + rand() % (end - begin + 1)
2. 针对全相等数组进行优化
当数组元素全部相等时,即使三数取中,Quicksort的时间复杂度仍然是
O
(
n
2
)
O(n{2})
O(n2)

根本原因是因为PartSort得到的keyi只区分了小于等于key和大于等于key的,只保证了小于等于key的在keyi左边,大于等于key的在keyi右边,因此当数组全部相等时,每次得到的keyi都是从0,1,2……n-1,每趟比较的次数就成等差数列。
我们可以使用三路划分来优化这种情况。
三路划分:将待排数据严格分为3部分,左边是小于key的数据,中间是等于key的数据,右边是大于key的数据。每次只递归左边和右边。当数组元素全部相等时,作区间不存在,右区间也不存在,因此递归左右区间一次就会停止排序。针对相等数组的时间复杂度为
O
(
n
)
O(n)
O(n),三路划分的本质是小的甩到左边,大的甩到右边。相等的推到中间
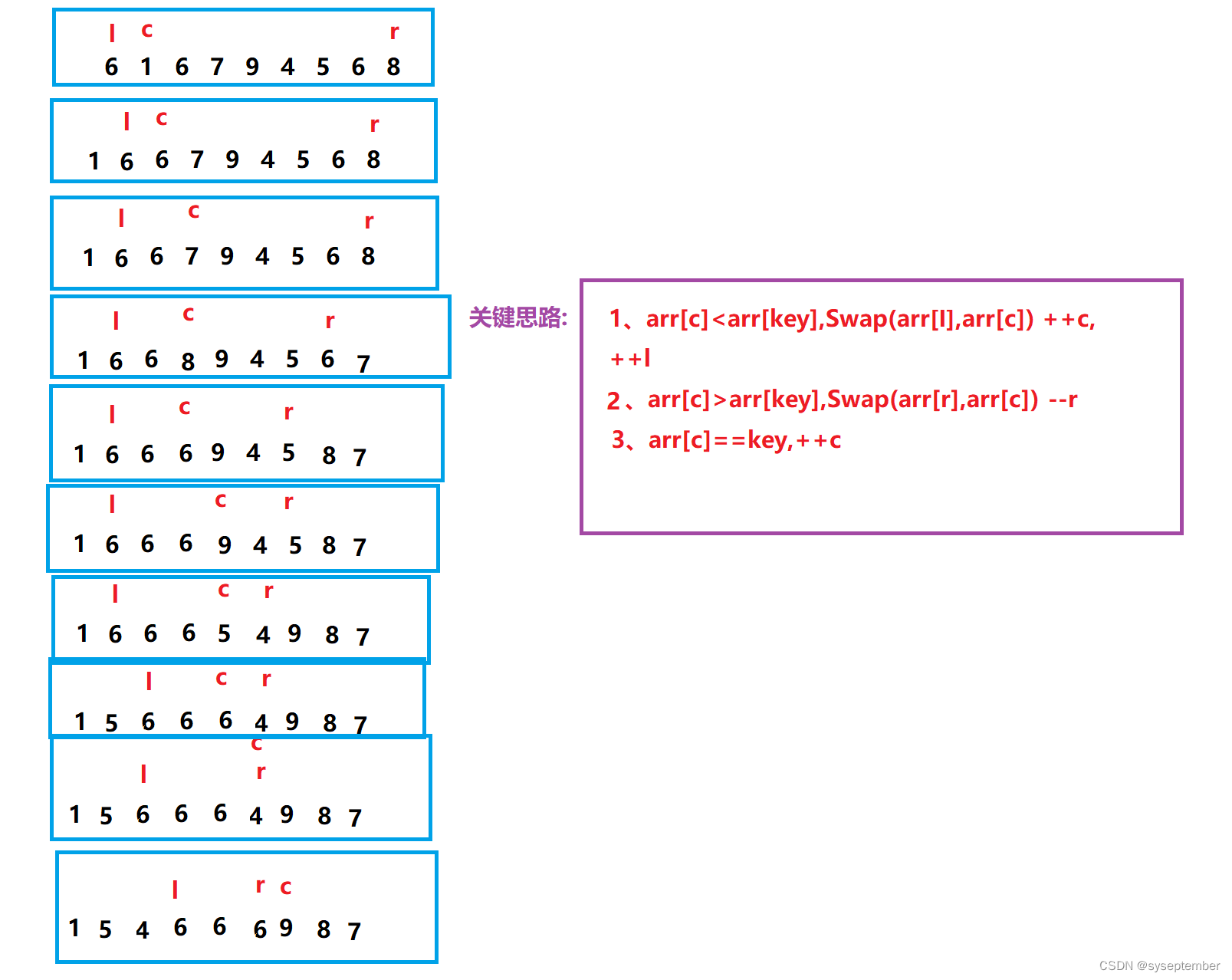
最后只需要递归区间[begin,l-1],[r + 1,end]即可
代码
//快排递归
void QuickSort(int* arr, int begin, int end)
{
//结束条件1.区间只有一个元素 2.区间不存在
if (end <= begin )
return;
// int midi = GetMidi(arr, begin, end);
int midi = begin + rand() % (end - begin + 1);//三数取中过不去使用随机数取中
Swap(&arr[begin], &arr[midi]);
//三路划分
int l = begin, c = begin + 1, r = end;
int key = arr[begin];
while (c <= r)
{
if (arr[c] > key)
{
Swap(&arr[c], &arr[r]);
r--;
}
else if (arr[c] < key)
{
Swap(&arr[c], &arr[l]);
l++,c++;
}
else c++;
}
//三路划分
QuickSort(arr, begin, l - 1);
QuickSort(arr, r + 1, end);
}
运行结果
算法分析
时间复杂度
| 快速排序 | 最好时间复杂度 | 最坏时间按复杂度 | 平均时间复杂度 |
|---|---|---|---|
| 递归快排(未优化) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^{2}) O(n2) | O ( n l o g n ) O(nlogn) O(nlogn) |
| 递归快排(优化) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) |
| 非递归快排(未优化) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^{2}) O(n2) | O ( n l o g n ) O(nlogn) O(nlogn) |
| 非递归快排(优化) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) |
对于单趟排序,不管哪一种方法实现一趟排序的时间复杂度都是 O ( n ) O(n) O(n)
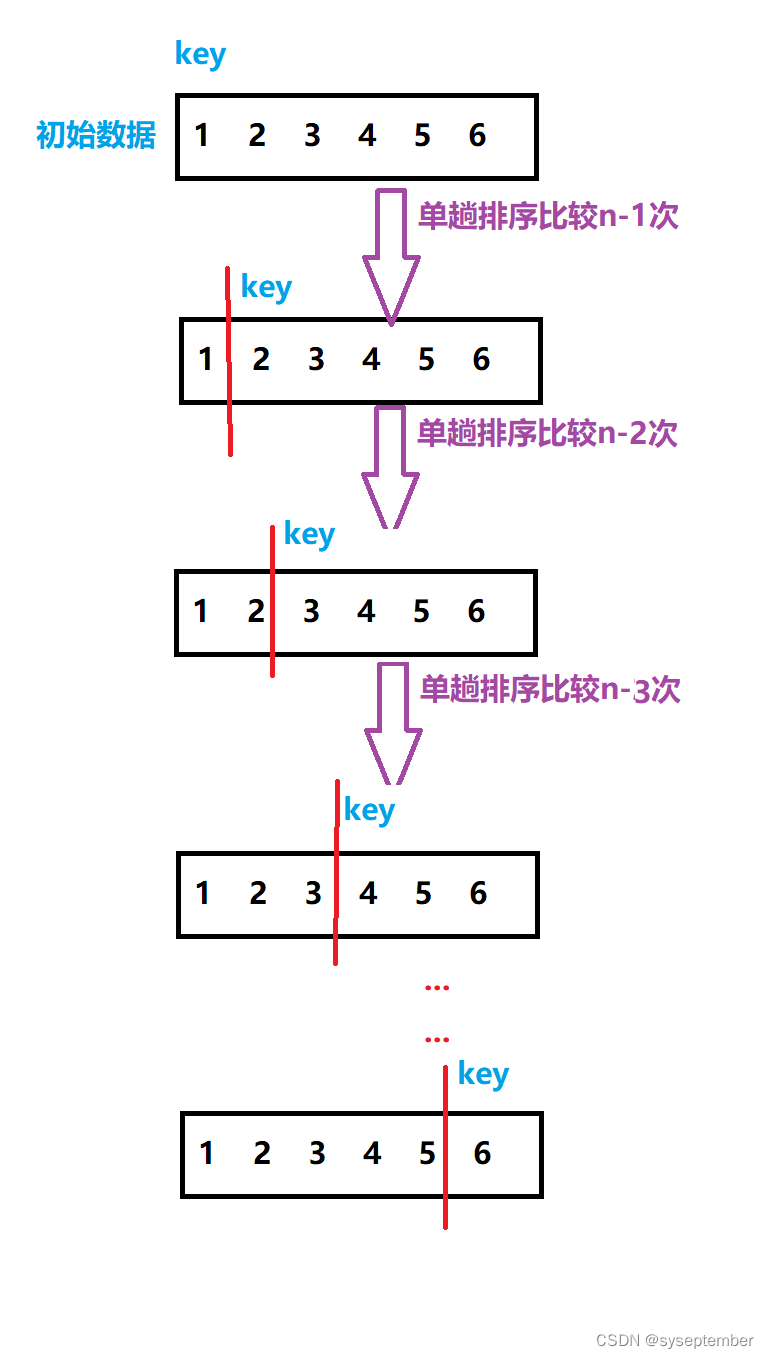
当待排数据本身有序时,如果没有优化,那么时间复杂度为
O
(
n
2
)
O(n^{2})
O(n2),因为每趟的比较次数为等差数列
空间复杂度
| 快速排序 | 空间复杂度 |
|---|---|
| 递归快速排序(未优化) | 最好 O ( l o g n ) O(logn) O(logn);最坏 O ( n ) O(n) O(n) |
| 递归快速排序(优化) | O ( l o g n ) O(logn) O(logn) |
| 非递归快速排序 | O ( 1 ) O(1) O(1) |

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BWAPI2s4-1689562847800)(C:\Users\石阳\AppData\Roaming\Typora\typora-user-images\image-20230712215303795.png)]](https://img-blog.csdnimg.cn/ea72956aaed344129a551a3c02baeab0.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Vlqb8Mvt-1689562622854)(C:\Users\石阳\AppData\Roaming\Typora\typora-user-images\image-20230712132400678.png)]](https://img-blog.csdnimg.cn/fc12d0478eb0436d9aca911f0e88a72f.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IA3sVEND-1689562622855)(C:\Users\石阳\AppData\Roaming\Typora\typora-user-images\image-20230712153642206.png)]](https://img-blog.csdnimg.cn/1895a904d30f436f81fb36dd99bf6320.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-43icCBTu-1689562622855)(C:\Users\石阳\AppData\Roaming\Typora\typora-user-images\image-20230712215450021.png)]](https://img-blog.csdnimg.cn/177ad46862ce4d4d879c1e097e22fe34.png)