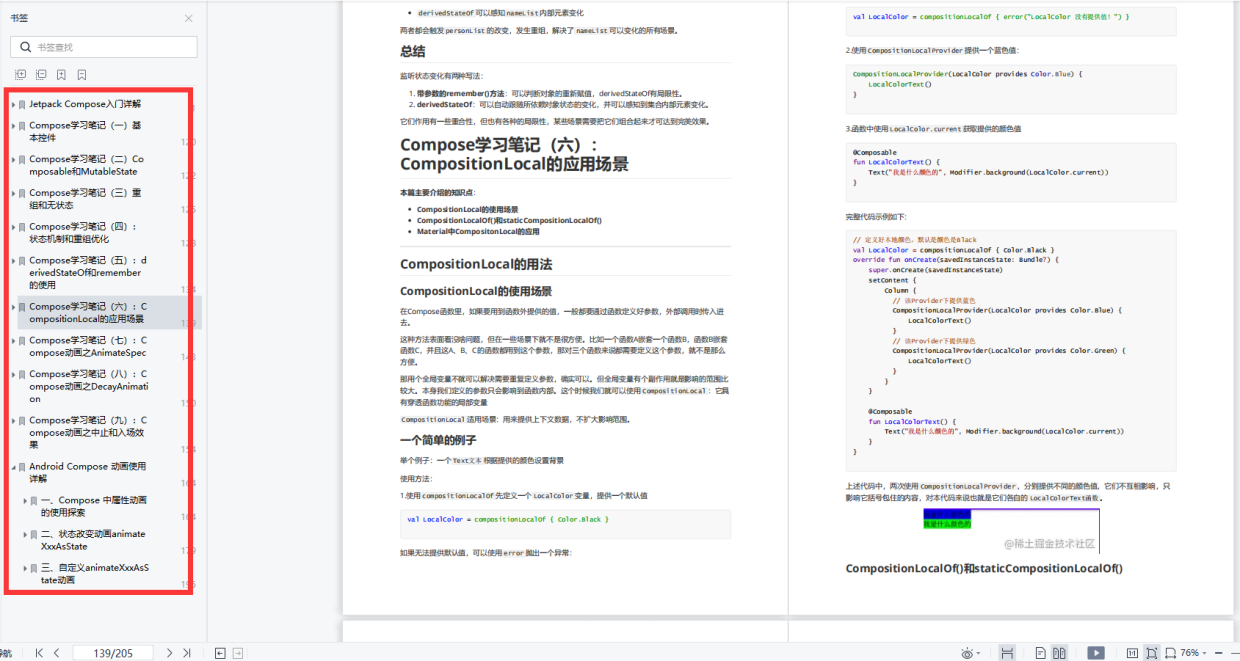
数据结构–图定义与基本术语

图的定义
图G由
顶点集
V
\color{red}顶点集V
顶点集V和
边集
E
\color{red}边集E
边集E组成,记为G = (V, E),其中V(G)表示图G中顶点的有限非空集;
E(G)表示图G中顶点之间的关系(边)集合。若
V
=
v
1
,
v
2
,
…
,
v
n
V = {v_1, v_2, … , v_n}
V=v1,v2,…,vn,则用|V|表示图G中顶点的个
数,也称图G的阶,
E
=
{
(
u
,
v
)
∣
u
∈
V
,
v
∈
V
}
E=\{(u,v)\mid u\in V,v\in V\}
E={(u,v)∣u∈V,v∈V},用|E|表示图G中边的条数。
注意:
线性表可以是空表,树可以是空树,但图不可以是空,即
V
一定是非空集
\color{green}线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集



图逻辑结构的应用


无向图、有向图

若E是
无向边
\color{red}无向边
无向边(简称
边
\color{red}边
边)的有限集合时,则图G为无向图。
边是顶点的无序对,记为
(
v
,
w
)
或
(
w
,
v
)
\color{red}(v, w)或(w, v)
(v,w)或(w,v),因为(v, w) = (w, v),其中v、w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v,或者说边(v, w)和顶点v、w相关联。
G 2 = ( V 2 , E 2 ) V 2 = { A , B , C , D , E } E 2 = { ( A , B ) , ( B , D ) , ( B , E ) , ( C , D ) , ( C , E ) , ( D , E ) } \begin{aligned} &G_{2} =(V_{2},E_{2}) \\ &V_{2} =\{A,B,C,D,E\} \\ &E_{2} =\{(A,B),(B,D),(B,E),(C,D),(C,E),(D,E)\} \end{aligned} G2=(V2,E2)V2={A,B,C,D,E}E2={(A,B),(B,D),(B,E),(C,D),(C,E),(D,E)}

若E是
有向边
\color{red}有向边
有向边(也称
弧
\color{red}弧
弧)的有限集合时,则图G为
有向图
\color{red}有向图
有向图。
弧是顶点的有序对,记为
<
v
,
w
>
\color{red}<v, w>
<v,w>,其中v、w是顶点,v称为
弧尾
\color{red}弧尾
弧尾,w称为
弧头
\color{red}弧头
弧头,<v, w>称为从顶点v到顶点w的弧,也称
v邻接到w,或w邻接自v。
<
v
,
w
>
≠
<
w
,
v
>
\color{red} <v, w> ≠ <w, v>
<v,w>=<w,v>
G 1 = ( V 1 , E 1 ) V 1 = { A,B,C,D,E } E 1 = { <A,B>,<A,C>,<A,D>,<A,E>,<B,A>,<B,C>,<B,E>,<C,D> \begin{array}{l}G_1=(V_1,E_1)\\V_1=\{\textsf{A,B,C,D,E}\}\\E_1=\{\textsf{<A,B>,<A,C>,<A,D>,<A,E>,<B,A>,<B,C>,<B,E>,<C,D>}\\\end{array} G1=(V1,E1)V1={A,B,C,D,E}E1={<A,B>,<A,C>,<A,D>,<A,E>,<B,A>,<B,C>,<B,E>,<C,D>
简单图、多重图
简单无向图:

简单有向图:

简单图
\color{red}简单图
简单图:
① 不存在重复边;
② 不存在顶点到自身的边
多重无向图:

多重有向图:

多重图
\color{red}多重图
多重图:
图G中某两个结点之间的边数多于
一条,又允许顶点通过同一条边和自己关联,
则G为多重图
顶点的度、入度、出度

对于
无向图
\color{red}无向图
无向图:
顶点
v
的度
\color{red}顶点v的度
顶点v的度是指依附于该顶点的边的条数,记为TD(v)。
在具有n个顶点、e条边的无向图中,
∑
i
=
1
n
T
D
(
v
i
)
=
2
e
\sum_{i=1}^n\mathrm{TD}(v_i)=2e
∑i=1nTD(vi)=2e
即无向图的全部顶点的度的和等于边数的2倍

对于
有向图
\color{red}有向图
有向图:
入度
\color{red}入度
入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v)。
顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)。
在具有n个顶点、e条边的有向图中,
∑
i
=
1
n
I
D
(
ν
i
)
=
∑
i
=
1
n
O
D
(
ν
i
)
=
e
\sum_{i=1}^n\mathrm{ID}(\nu_i)=\sum_{i=1}^n\mathrm{OD}(\nu_i)=e
∑i=1nID(νi)=∑i=1nOD(νi)=e
顶点-顶点的关系描述
顶点之间有可能不存在路径:

有向图的路径也是有向的:

•
路径
\color{red}路径
路径——顶点vp到顶点vq之间的一条路径是指顶点序列 ,
v
p
,
v
i
1
,
v
i
2
,
⋯
,
v
i
m
,
v
q
v_{p},v_{i_{1}},v_{i_{2}},\cdots,v_{i_{m}},v_{q}
vp,vi1,vi2,⋯,vim,vq
•
回路
\color{red}回路
回路——第一个顶点和最后一个顶点相同的路径称为回路或环
•
简单路径
\color{red}简单路径
简单路径——在路径序列中,顶点不重复出现的路径称为简单路径。
•
简单回路
\color{red}简单回路
简单回路——除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
•
路径长度
\color{red}路径长度
路径长度——路径上边的数目
•
点到点的距离
\color{red}点到点的距离
点到点的距离——从顶点u出发到顶点v的
最短路径
\color{red}最短路径
最短路径若存在,则此路径的长度称为从u到v的距离。
若从u到v根本
不存在路径
\color{red}不存在路径
不存在路径,则
记该距离为无穷(
∞
)
\color{red}记该距离为无穷(∞)
记该距离为无穷(∞)。
•
无向图
\color{red}无向图
无向图中,若从顶点v到顶点w有路径存在,则称v和w是
连通
\color{red}连通
连通的
•
有向图
\color{red}有向图
有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是
强连通
\color{red}强连通
强连通的
连通图、强连通图

若图G中任意两个顶点都是连通的,则称图G为
连通图,否则称为非连通图。
若图中任何一对顶点都是强连通的,则称此图为强连通图。
常见考点:
\color{red}常见考点:
常见考点:
对于n个顶点的无向图G,
若G是
连通图
\color{red}连通图
连通图,则
最少
\color{red}最少
最少有 n-1 条边
若G是
非连通图
\color{red}非连通图
非连通图,则
最多
\color{red}最多
最多可能有
C
n
−
1
2
C_{n-1}^2
Cn−12 条边

若图中任何一对顶点都是强连通的,则称此图为
强连通图
\color{red}强连通图
强连通图。
常见考点
\color{red}常见考点
常见考点:
对于n个顶点的有向图G,
若G是
强连通图
\color{red}强连通图
强连通图,则
最少
\color{red}最少
最少有 n 条边(形成回路)
研究图的局部——子图
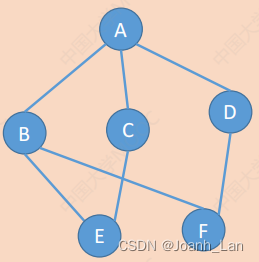


设有两个图G =(V,E)和G′ =(V’,E’),若V’是V的子集,且E′是E的子集,则称G’是G的 子图 \color{red}子图 子图
若有满足V(G’)=V(G)的子图G’9则称其为G的 生成子图 \color{red}生成子图 生成子图
并非任意挑几个点、几条边都能构成子图 \color{green}并非任意挑几个点、几条边都能构成子图 并非任意挑几个点、几条边都能构成子图

连通分量
无向图中的 极大连通子图 \color{red}极大连通子图 极大连通子图称为连通分量。
极大连通子图:子图必须连通,且包含尽可能多的顶点和边
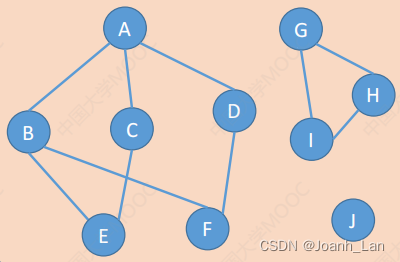
G的三个连通分量:



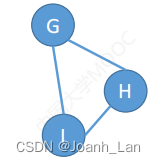
强连通分量
强连通分量(Strongly Connected Component,简称SCC)是指有向图中的一个子图,其中 任意两个顶点之间都存在有向路径 \color{red}任意两个顶点之间都存在有向路径 任意两个顶点之间都存在有向路径。

G的三个强连通分量:



生成树
连通图
\color{red}连通图
连通图的
生成树
\color{red}生成树
生成树是
包含图中全部顶点的一个极小连通子图
\color{red}包含图中全部顶点的一个极小连通子图
包含图中全部顶点的一个极小连通子图。
若图中顶点数为n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。

G的生成树:


生成森林
在 非连通图 \color{red}非连通图 非连通图中, 连通分量的生成树 \color{red}连通分量的生成树 连通分量的生成树构成了非连通图的 生成森林 \color{red}生成森林 生成森林。

G的连通分量 → \to →G的生成森林


边的权、带权图/网
给各边赋予一个权值——实际距离

给各边赋予一个数值——转发概率

边的权
\color{red}边的权
边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。
带权图
/
网
\color{red}带权图/网
带权图/网——边上带有权值的图称为
带权图
\color{red}带权图
带权图,也称
网
\color{red}网
网。
带权路径长度
\color{red}带权路径长度
带权路径长度——当图是带权图时,一条
径上所有边的权值之和
\color{red}径上所有边的权值之和
径上所有边的权值之和,称为该路径的带权路径长度
几种特殊形态的图
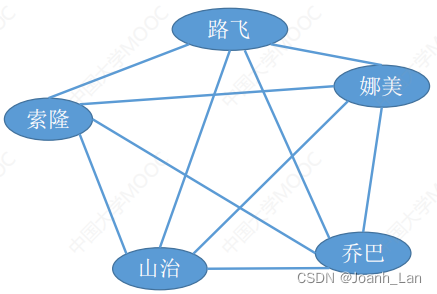
无向完全图 \color{red}无向完全图 无向完全图——无向图中任意两个顶点之间都存在边
若无向图的顶点数|V|=n,则 ∣ E ∣ ∈ [ 0 , C n 2 ] = [ 0 , n ( n − 1 ) / 2 ] |E|\in[0,C_n^2]=[0,\color{red}{n(n-1)/2}] ∣E∣∈[0,Cn2]=[0,n(n−1)/2]

有向完全图
\color{red}有向完全图
有向完全图——有向图中任意两个顶点
之间都存在方向相反的两条弧
若有向图的顶点数|V|=n,则
∣
E
∣
∈
[
0
,
2
C
n
2
]
=
[
0
,
n
(
n
−
1
)
]
|E|\in[0,2C_n^2]=[0,\color{red}{n(n-1)}]
∣E∣∈[0,2Cn2]=[0,n(n−1)]

边数很少的图称为 稀疏图 \color{red}稀疏图 稀疏图

反之称为 稠密图 \color{red}稠密图 稠密图
没有绝对的界限,一般来说|E| < |V|log|V|时,可以将G视为稀疏图

树 \color{red}树 树—— 不存在回路 \color{red}不存在回路 不存在回路,且 连通 \color{red}连通 连通的 无向图 \color{red}无向图 无向图
n个顶点的树,必有n-1条边。
常见考点:n个顶点的图,
若
∣
E
∣
>
n
−
1
,则一定有回路
\color{red}若 |E|>n-1,则一定有回路
若∣E∣>n−1,则一定有回路

有向树
\color{red}有向树
有向树——一个顶点的入度为0、其余顶点的
入度均为1的
有向图
\color{red}有向图
有向图,称为有向树。
知识回顾与重要考点

常见考点:
对于n个顶点的
无向图
\color{red}无向图
无向图G,
• 所有顶点的度之和=2|E|
• 若G是连通图,则最少有 n-1 条边(树),若 |E|>n-1,则一定有回路
• 若G是非连通图,则最多可能有
C
n
−
1
2
C_{n-1}^2
Cn−12
• 无向完全图共有
C
n
2
C_{n}^2
Cn2条边
对于n个顶点的
有向图
\color{red}有向图
有向图G,
• 所有顶点的出度之和=入度之和=|E|
• 所有顶点的度之和=2|E|
• 若G是强连通图,则最少有 n 条边(形成回路)
• 有向完全图共有
2
C
n
2
2C_{n}^2
2Cn2 条边