系列文章目录
基于scrcpy的远程调试方案
基于scrcpy的Android群控项目重构
基于scrcpy的Android群控项目重构 进阶版
基于scrcpy的Android群控项目重构,获取Android屏幕元素信息并编写自动化事件(视频)
基于scrcpy的Android群控项目重构,获取Android屏幕元素信息并编写自动化事件(博客)
基于scrcpy的Android群控项目重构,集成Appium服务执行自动化测试用例(视频)
基于scrcpy的Android群控项目重构,集成Appium服务执行自动化测试用例(博客)
文章目录
系列文章目录
前言
一、获取元素信息
二、编写测试用例
1.选取元素信息
2.添加事件
视频示例
前言
Android获取屏幕元素信息解析并在前端结构化展示,通过获取到的元素编写自动话脚本,执行测试用例,只支持在本地环境运行;
Spring Boot + MySQL + Redis + Java + Layui模板
一、获取元素信息
进入后台筛选可用设备,点击投屏,进入投屏页面,投屏成功后点击【获取元素信息】后就可以展示元素信息,并且截图当前屏幕并在右边展示,根据需求获取需要的元素信息,如下图显示

二、编写测试用例
1.选取元素信息
在第一步选取元素信息,如下图元素信息框

2.添加事件
点击【事件管理】进入列表页,在格顶部工具栏新增或者在表格中新增都可以添加新的事件,事件分为主事件和子事件。
主事件:一条测试用例的第一个事件,且一条测试用例只有一个主事件。
子事件:一条测试用例的非第一个事件,且一条测试用例可以有多个子事件,也可以没有子事件。
如图所示表格顶部工具栏【新增】,这个只能新增主事件

如图所示表格中【新增】,这个可以新增主事件和子事件

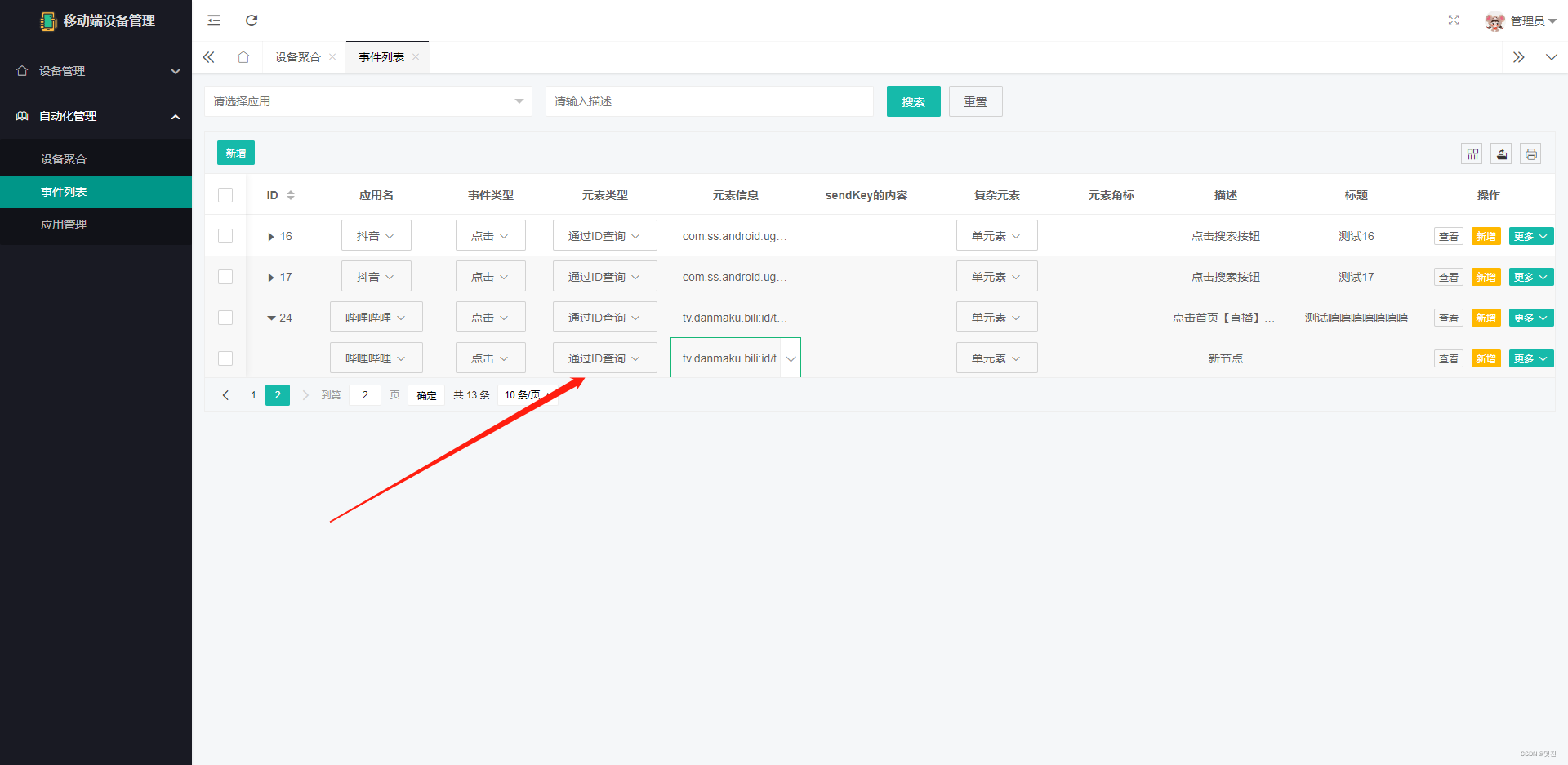
如图所示直接在表格中【修改】事件

视频示例
基于scrcpy的Android群控项目重构,获取Android屏幕元素信息并编写自动化事件