不均衡数据
很多时候,不同类别的分类代价并不相等,这就是非均衡分类问题。如果在两个类别中,一个类别的出现次数比另一个多很多,那么错误类型将发挥重要作用。例如。我们一共有100个病人,其中99人是健康的(阴性、反类),1人是患癌症的(阳性、正类),那么这种数据集就是不平衡数据集(imbalanced dataset)或者具有不平衡类别的数据集(dataset with imbalanced classes)。在实际当中,不平衡数据才是常态。在这个数据集中,我们即使预测得到99%的分类精度,也不代表我们模型的泛化性能就好。有一种可能·就是,我们把99个健康的预测正确了,而1个患病的没有预测正确。
混淆矩阵

真正例(TP):true positive,将正类中正确分类的样本。
真反例(TN):true negative,将反类中正确分类的样本。
假正例(FP):false positive,反类预测为正类的样本。
假反例(FN):false negative,正类预测为反类的样本。
Accuracy
模型的精度,即模型预测正确的个数/样本的总个数

准确率
正确率,阳性预测值,在模型预测为正类的样本中,真正的正样本所占的比例
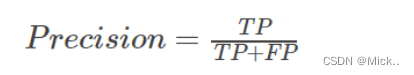
召回率
度量的是正类样本中有多少被预测为正类
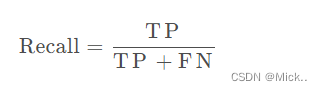
Recall越高,说明有更多的正类样本被模型预测正确,模型的效果越好。
f-分数
将准确率和召回率进行汇总的一种方法是f-分数(f-score)或f-度量(f-measure),它是准确率与召回率的调和平均


由于同时考虑了准确率和召回率,所以它对于不平衡的二分类数据集来说是一种比精度更好的度量。
ROC曲线

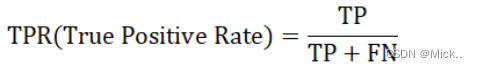
TPR是学习器分类正确的正实例占所有样本正实例的比例
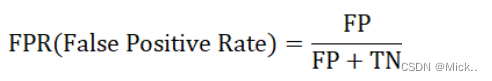
FPR是指学习器分类正确占所有样本反例的比例
ROC曲线x轴是TPR,表示的是正确率,y轴是FPR,表示的是假阳。
from sklearn.svm import SVC
from sklearn.metrics import roc_curve
from sklearn.datasets import make_blobs
from sklearn. model_selection import train_test_split
import matplotlib.pyplot as plt
# make_blobs函数,生成一个二分类的数据不平衡数据集
X, y = make_blobs(n_samples=(4000, 500), cluster_std=[7, 2], random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = SVC(gamma=0.05).fit(X_train, y_train)
fpr, tpr, thresholds = roc_curve(y_test, clf.decision_function(X_test))
plt.plot(fpr, tpr, label='ROC')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.show()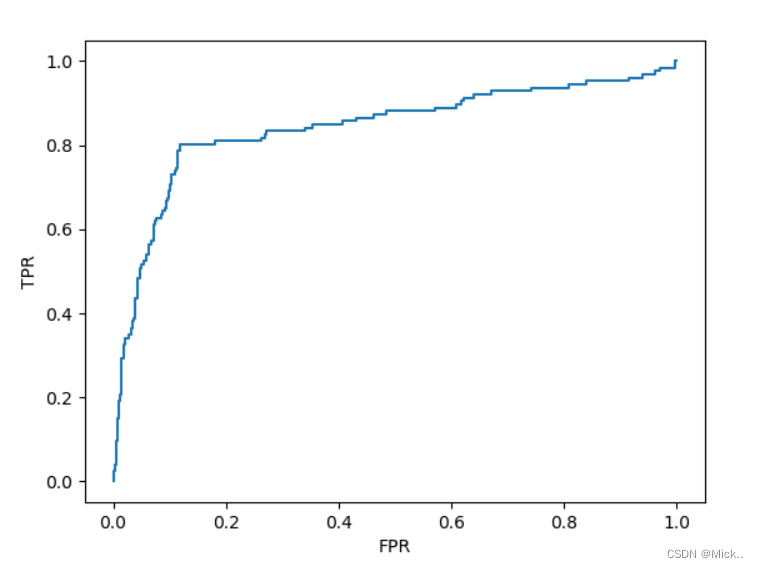
from sklearn.svm import SVC
from sklearn.metrics import roc_curve,roc_auc_score
from sklearn.datasets import make_blobs
from sklearn. model_selection import train_test_split
import matplotlib.pyplot as plt
# make_blobs函数,生成一个二分类的数据不平衡数据集
X, y = make_blobs(n_samples=(4000, 500), cluster_std=[7, 2], random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = SVC(gamma=0.05).fit(X_train, y_train)
# auc = roc_auc_score(y_test,clf.predict_proba(X_test)[:,1])
auc = roc_auc_score(y_test,clf.decision_function(X_test))
fpr,tpr, thresholds = roc_curve(y_test,clf.decision_function(X_test))
plt.plot(fpr,tpr,color='darkorange',label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.savefig('suhan.jpg',dpi=800)
plt.show() 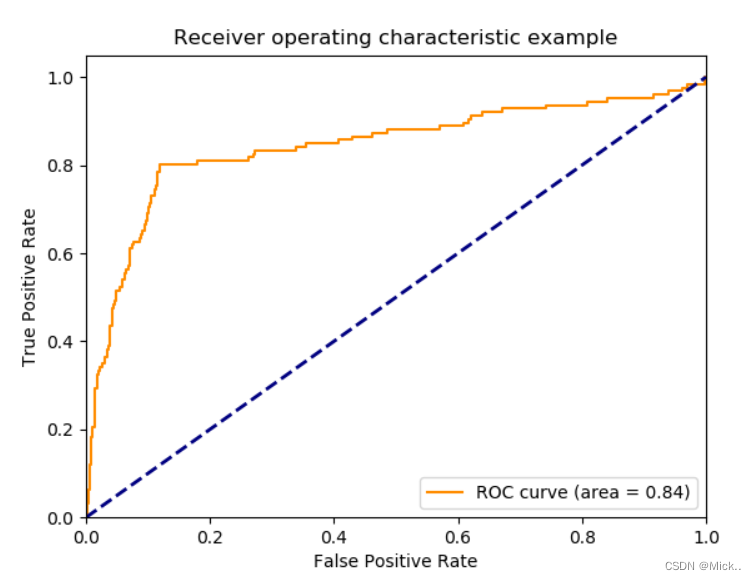
参考文献:
5分钟带你学懂ROC曲线_最强理发师托尼的博客-CSDN博客_roc曲线









![[附源码]Python计算机毕业设计SSM基于人脸识别和测温的宿舍管理系统(程序+LW)](https://img-blog.csdnimg.cn/0cee7d35168d482e813b5e847af669ae.png)