【改进粒子群优化算法】基于惯性权重和学习因子动态调整的粒子群算法【期刊论文复现】（Matlab代码实现）

news2024/11/24 12:45:56

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

效果图：

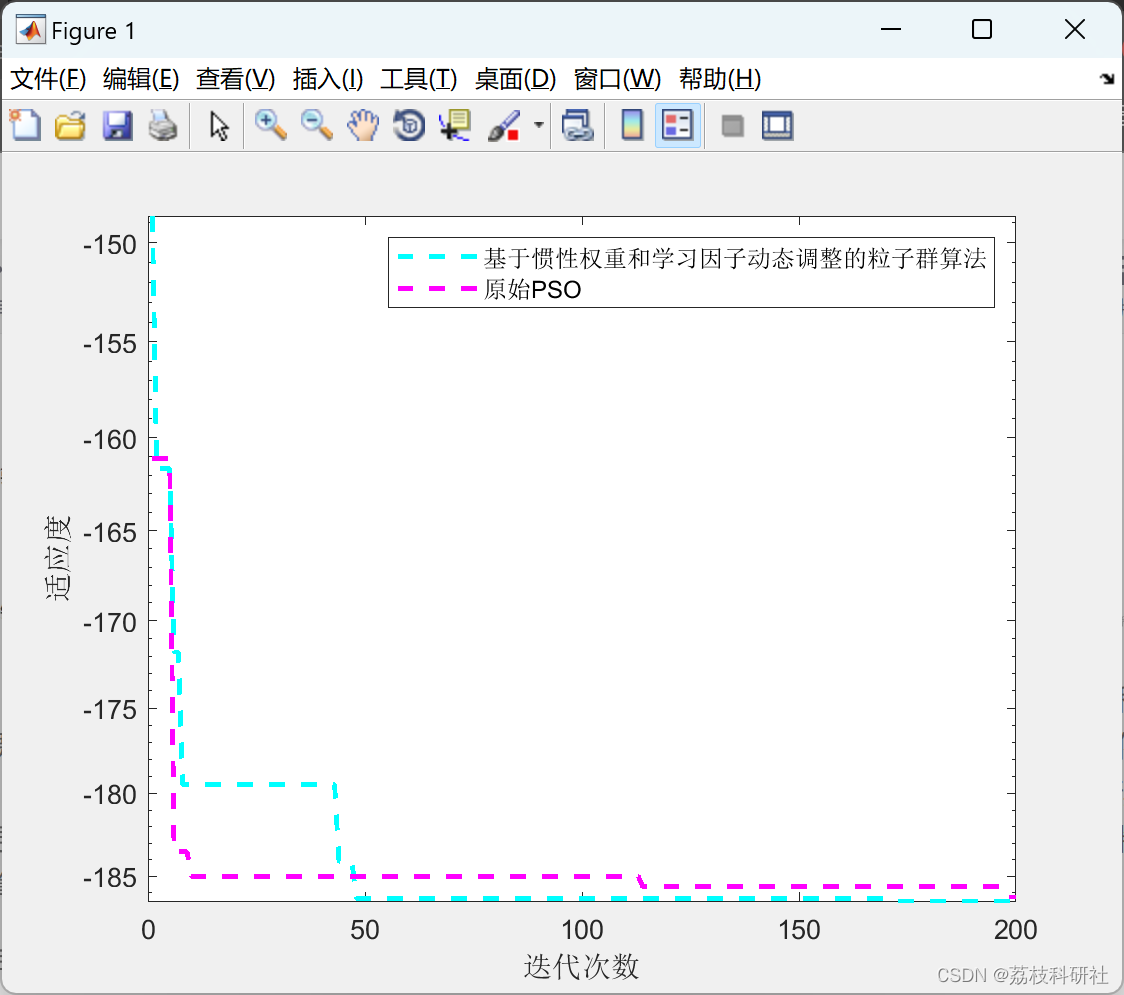
💥1 概述

部分代码：

摘要：针对传统的粒子群算法易发生早熟收敛、在寻优过程中易陷入局部最优等问题,提出了一种基于惯性权重和学习因子动态调整的粒子群算法,该算法通过改进惯性权重和学习因子参数以优化算法。随着算法的不断迭代,其惯性权重以及学习因子随着迭代次数的增加而动态优化,从而平衡其局部寻优能力与全局搜索能力。实验结果表明,改进后的算法在收敛速度以及收敛精度上比传统粒子群算法更优,能改善早熟收敛问题。

关键词：

粒子群算法;动态调整;迭代;优化;惯性权重;学习因子;

📚2 运行结果

部分代码：

for i=1:nPop%种群位置、速度、适应度初始化
pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
pop(i).Velocity = unifrnd(Vmin, Vmax, VarSize);
pop(i).Cost = fun(pop(i).Position,index);
if pop(i).Cost < pBestSol.Cost
pBestSol = pop(i);%个体适应度最佳
end
end
gBestSol = pBestSol;
for it=1:MaxIt
for i=1:nPop
w = 1+(1-0.7).*(it.^2)/(MaxIt^2);
c1 = (1-0.7).*it/MaxIt+0.7;
c2 = (1-0.7).*it/MaxIt+0.7;
%速度更新
pop(i).Velocity = w.*pop(i).Velocity+c1.*rand(VarSize).*(pBestSol.Position-pop(i).Position)+c2.*rand(VarSize).*(gBestSol.Position-pop(i).Position);
%速度边界处理
pop(i).Velocity = max(pop(i).Velocity, Vmin);
pop(i).Velocity = min(pop(i).Velocity, Vmax);
%位置更新
pop(i).Position = pop(i).Position+pop(i).Velocity;
%位置边界处理
pop(i).Position = max(pop(i).Position, VarMin);
pop(i).Position = min(pop(i).Position, VarMax);
%适应度值更新
pop(i).Cost = fun(pop(i).Position,index);
%更新局部最优
if pop(i).Cost < pBestSol.Cost
pBestSol = pop(i);
%更新全局最优
if pBestSol.Cost < gBestSol.Cost
gBestSol = pBestSol;
end
end
BestCosts(it) = gBestSol.Cost;
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
end
end
IPSO_polbelbest = pBestSol;