内容：堆排序的代码实现及注解，思路详解

代码实现：

交换函数：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

堆排序函数：

1 向下调整建堆函数：这里建立大堆，小堆思路也是类似的

   找出孩子中最小的一个与父节点比较，若是最小的孩子小于父亲，交换二者，父节点继续比较，可能存在多次向下调整，直至调整至合适的位置或者调无可调

若是最小的孩子大于父节点，则无需向下调整

http://t.csdn.cn/SwZaB 这里是我另一篇关于堆向下调整算法的详解，这里不做过多赘述

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//建大堆-假设左孩子是两孩子中较大的一个
	while (child < n)//可能存在多次向下调整，当父节点调整至叶子节点时（即无孩子）无需再向下调整
	{
		if (child + 1 < n && a[child + 1] > a[child])//找出左右孩子中较大的一个，（右孩子存在的前提下）
		{
			child++;//右孩子大，将child调整为右孩子的下标
		}

		if (a[child] > a[parent])//若是父节点小于最大的孩子节点，向下调整，交换二者
		{
			Swap(&a[child], &a[parent]);
			parent = child;//构成循环
			child = parent * 2 + 1;
		}
		else//父节点大于最大的孩子节点，无需向下调整
		{
			break;
		}
	}
}

2 堆排序函数：

void HeapSort(int* a, int n)//升序-建大堆
{
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--)//向下调整建立大堆
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)//将堆顶值逐个与数组后面的元素交换
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);//向调整，使得堆顶值为堆中元素的最大值
		end--;
	}
}

 

 

 

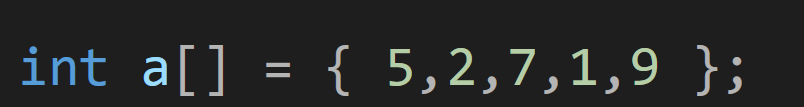
思路详解：

堆排序分成两部分：

1 建堆

2 从数组后面的元素开始，堆顶元素与之一一交换

关于建堆：

升序：需要建立大堆

因为大堆的堆顶元素总是堆中元素的最大值，交换到数组的后面，完成后就是升序了

最大值交换到最后，调堆得第二大值，交换到倒数第二个位置，调堆得第三大值，交换到倒数第三个位置……

降序：需要建立小堆

因为大堆的堆顶元素总是堆中元素的最小值，交换到数组的后面，完成后就是降序了

最小值交换到最后，调堆得第二小值，交换到倒数第二个位置，调堆得第三小值，交换到倒数第三个位置……

关于交换：

 建好堆后，堆顶元素就是最大值/最小值，从数组最后一个元素位置开始，依次将每个堆顶元素与之交换，每一次交换完成后，将交换到数组后面的原堆顶元素隔离开，不再看作堆中元素，然后对剩下的看作堆中的元素进行向下调整（从堆顶元素开始），使之任然构成一个大堆。

图示：

下图是数组建立好大堆的逻辑结构：

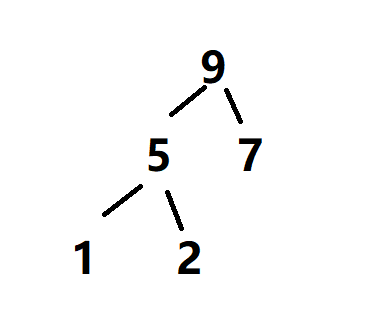
 数组建成大堆的物理结构：

 

 

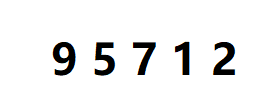
 次数9的下标就是看作堆中元素的个数，要对它们从堆顶元素开始向下调整

因为堆顶元素是新交换过来的，不能够确定它的大小，所以需要向下调整使之仍然保持大堆结构

调堆： 逻辑结构  这里的调堆为了方便，不再对非看作堆中元素的值进行调堆过程中的显示

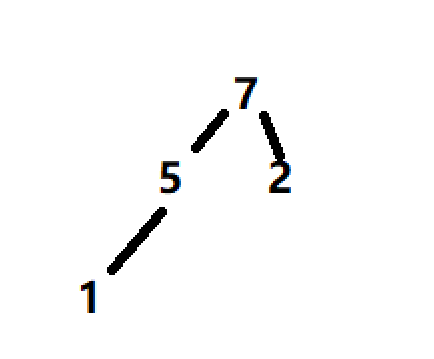
 物理结构：

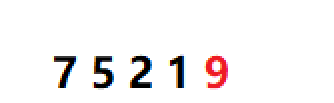
 将堆顶元素交换：

调整：逻辑结构 

 

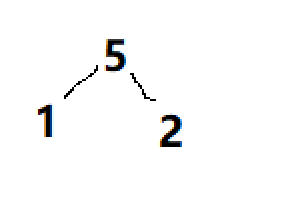
物理结构：

 

 将堆顶元素交换：

调堆：逻辑结构

 

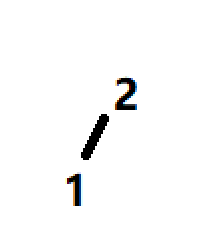
物理结构：将2与1交换之后的图：

 完结撒花~