16. 最接近的三数之和

16. 最接近的三数之和

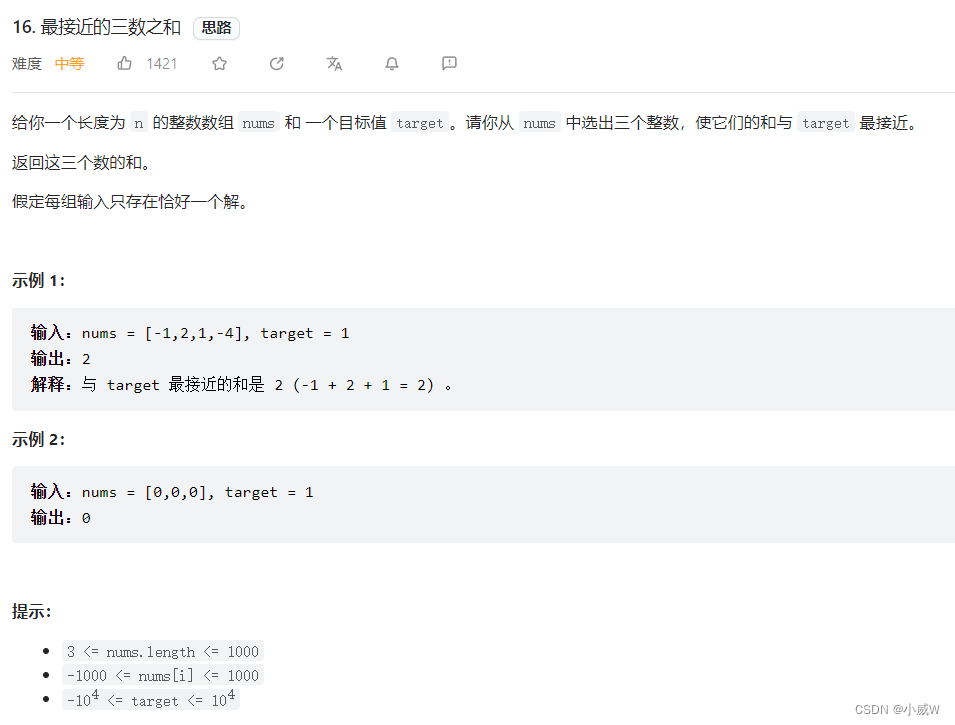
排序 + 双指针

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int n = nums.length, mn = Integer.MAX_VALUE, ans = 0;
        Arrays.sort(nums);
        for (int i = 0; i < n - 2; ++i) {
            for (int l = i + 1, r = n - 1; l < r; ) {
                int sum = nums[i] + nums[l] + nums[r];
                int diff = Math.abs(sum - target);
                if (diff < mn) {
                    mn = diff;
                    ans = sum;
                }

                if (sum < target) ++l;
                else if (sum > target) --r;
                else return ans;
            }
        }
        return ans;
    }
}

时间复杂度控制在$O(n^2)$

1911. 最大子序列交替和

1911. 最大子序列交替和

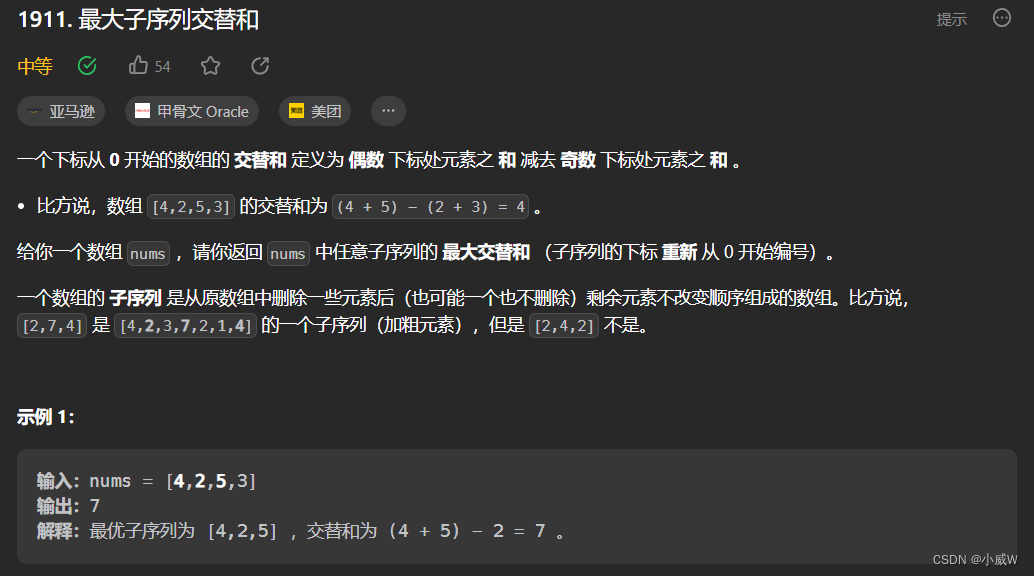
解法——动态规划

1. dp[i][0]和dp[i][1]分别表示以i为结果做加法和做减法的最大值
2. 递推公式见代码
3. dp数组初始化dp[0]即可
4. 从前向后遍历

class Solution {
    public long maxAlternatingSum(int[] nums) {
        int n = nums.length;
        long[][] dp = new long[n][2];
        dp[0][0] = nums[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + nums[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - nums[i]);
        }
        return Math.max(dp[n - 1][0], dp[n - 1][1]);
    }
}

这题很类似 122. 买卖股票的最佳时机 II
，只不过可以在没有股票的情况下先卖一个。
这种思想写出来的代码如下：

class Solution {
    public long maxAlternatingSum(int[] prices) {
        int n = prices.length;
        long sell = prices[0], buy = 0;
        for (int i = 1; i < n; ++i) {
            long newSell = Math.max(sell, buy + prices[i]);
            buy = Math.max(buy, sell - prices[i]);
            sell = newSell;
        }
        return sell;
    }
}

2544. 交替数字和（简单模拟）

https://leetcode.cn/problems/alternating-digit-sum/

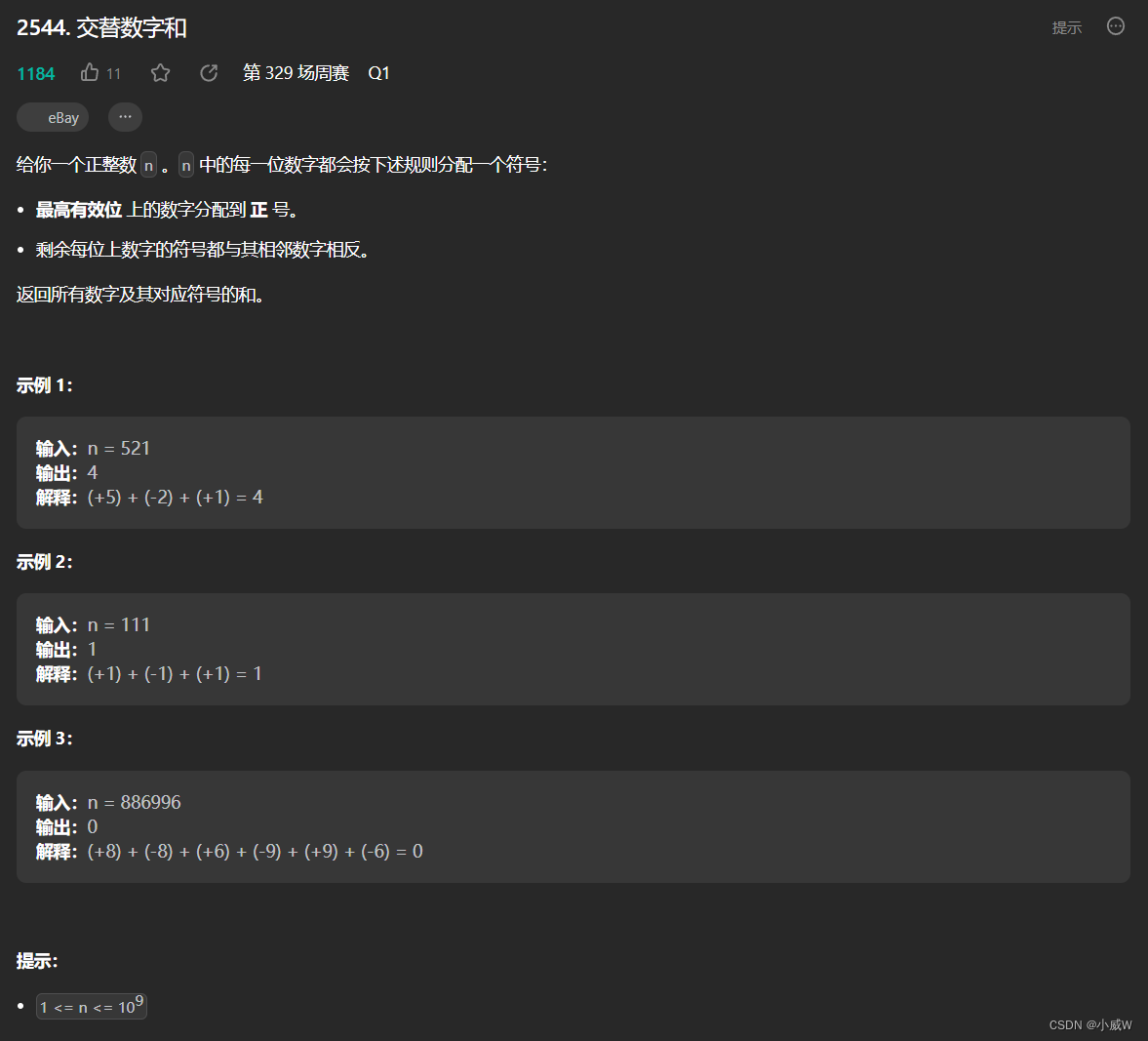
简单模拟即可。

 class Solution {
    public int alternateDigitSum(int n) {
        int sign = 1, ans = 0;
        while (n != 0) {
            ans += sign * (n % 10);
            n /= 10;
            sign *= -1;
        }
        return -sign * ans;
    }
}

931. 下降路径最小和（线性DP）

https://leetcode.cn/problems/minimum-falling-path-sum/

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[][] dp = new int[m][n];
        dp[0] = Arrays.copyOf(matrix[0], n);
        for (int i = 1; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                dp[i][j] = dp[i - 1][j];
                if (j - 1 >= 0) dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
                if (j + 1 < m) dp[i][j] = Math.min(dp[i][j], dp[i - 1][j + 1]);
                dp[i][j] += matrix[i][j];
            }
        }
        return Arrays.stream(dp[m - 1]).min().getAsInt();
    }
}

979. 在二叉树中分配硬币⭐⭐⭐⭐⭐（dfs）

https://leetcode.cn/problems/distribute-coins-in-binary-tree/

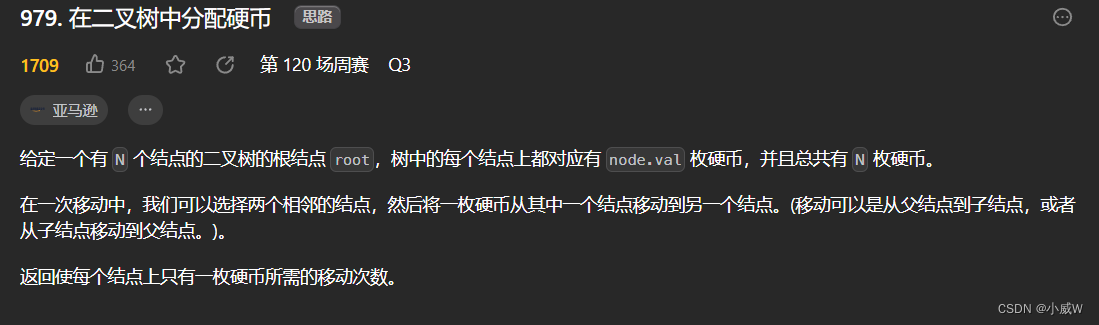
提示：
1<= N <= 100
0 <= node.val <= N

没有靠自己第一眼就做出来！

dfs (root) 的返回值表示 root 的父节点需要从 root 节点拿走几个金币才能让 root 处的金币数量为 1。

https://leetcode.cn/problems/distribute-coins-in-binary-tree/solutions/2339545/zai-er-cha-shu-zhong-fen-pei-ying-bi-by-e4poq/

class Solution {
    int ans = 0;

    public int distributeCoins(TreeNode root) {
        dfs(root);
        return ans;
    }

    // 返回值是root的父节点需要从root拿走几个金币才能让root是1
    public int dfs(TreeNode root) {
        int moveLeft = 0, moveRight = 0;
        if (root == null) return 0;
        if (root.left != null) moveLeft = dfs(root.left);
        if (root.right != null) moveRight = dfs(root.right);
        ans += Math.abs(moveLeft) + Math.abs(moveRight);
        return moveLeft + moveRight + root.val - 1;
    }
}

算法分析

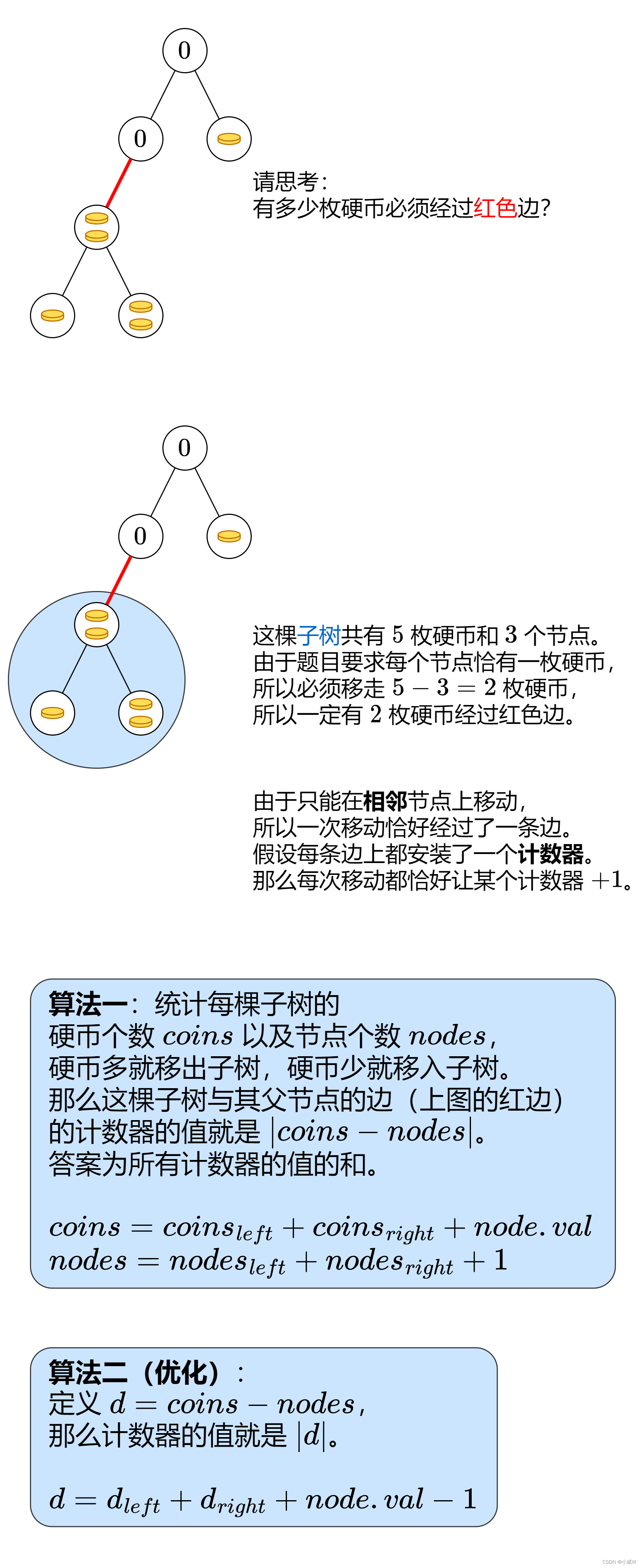
路径是由边组成的，所有路径长度之和，等同于把「每条边出现在多少条路径中」相加。这种技巧叫做贡献法。

补充：贡献法相关题目练习

更多题目可见：【算法】贡献法相关题目练习

891. 子序列宽度之和

https://leetcode.cn/problems/sum-of-subsequence-widths/

思路：

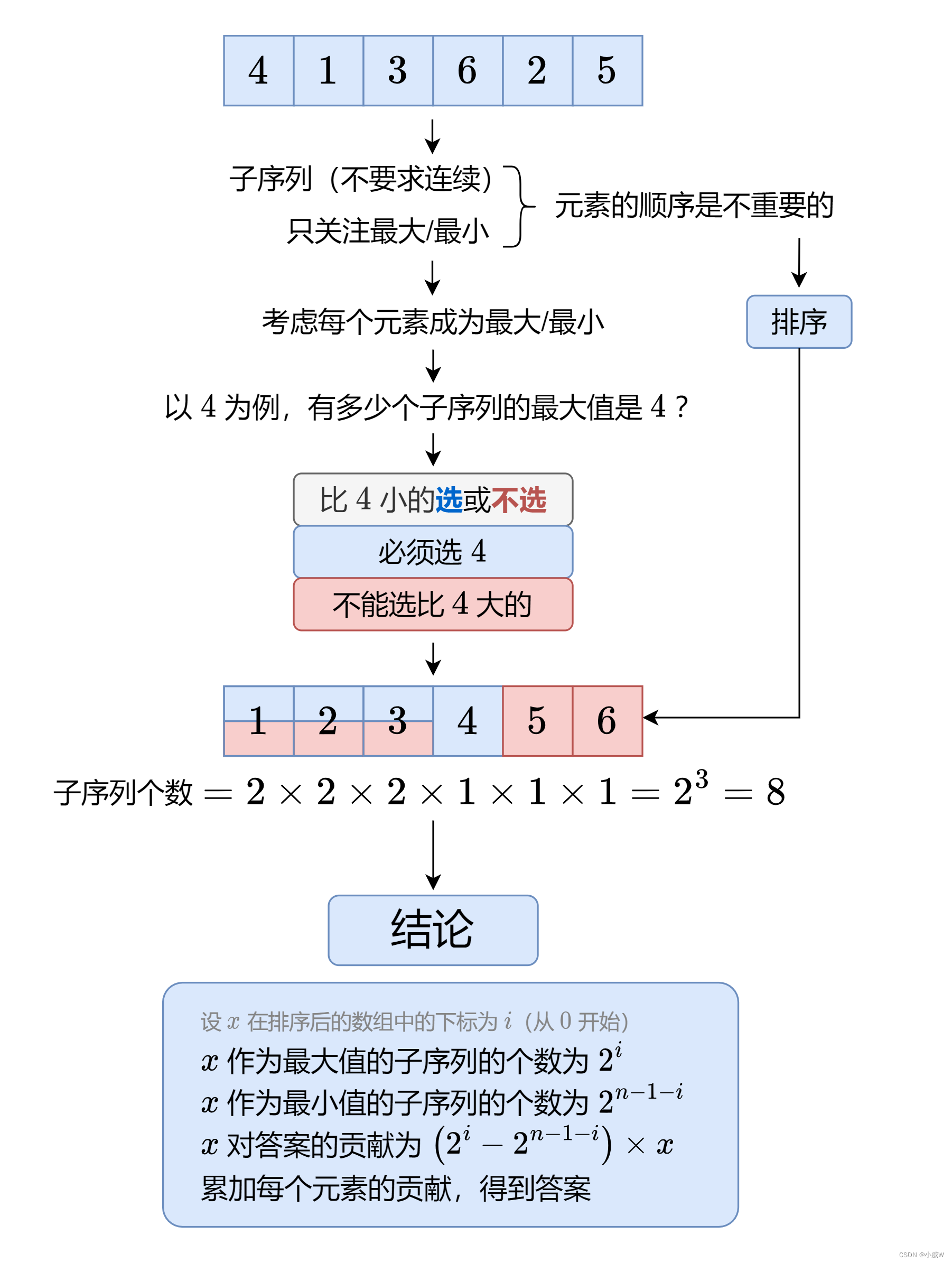
考虑每个元素会作为几个子序列的最小值，又会作为几个子序列的最大值。

class Solution {
    public int sumSubseqWidths(int[] nums) {
        final int MOD = (int)1e9 + 7;
        Arrays.sort(nums);          // 看到是序列，和顺序无关，可以排序！
        int n = nums.length;
        // 预处理出 2 的幂次
        int[] pow2 = new int[n];
        pow2[0] = 1;
        for (int i = 1; i < n; ++i) {
            pow2[i] = pow2[i - 1] * 2 % MOD;
        }
        long ans = 0;
        for (int i = 0; i < n; ++i) {
            // 计算 nums[i] 作为最大值的贡献减去作为最小值的贡献
            ans = (ans + (long)(pow2[i] - pow2[n - 1 - i]) * nums[i]) % MOD;
        }
        return (int)(ans + MOD) % MOD;
    }
}

18. 四数之和（排序 + 双指针 + 去重 + long）

18. 四数之和

排序 + 双指针 + 去重 + long

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ans = new ArrayList();
        Arrays.sort(nums);
        int n = nums.length;
        for (int i = 0; i < n - 3; ++i) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1; j < n - 2; ++j) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue; 
                long t = (long)target - nums[i] - nums[j];
                for (int l = j + 1, r = n - 1; l < r; ) {
                    if (l > j + 1 && nums[l] == nums[l - 1]) {
                        ++l;
                        continue;
                    }
                    long x = nums[l] + nums[r];
                    if (x < t) l++;
                    else if (x > t) r--;
                    else ans.add(List.of(nums[i], nums[j], nums[l++], nums[r--]));
                }
            }
        }
        return ans;
    }
}

834. 树中距离之和⭐⭐⭐⭐⭐（两次 dfs）

834. 树中距离之和

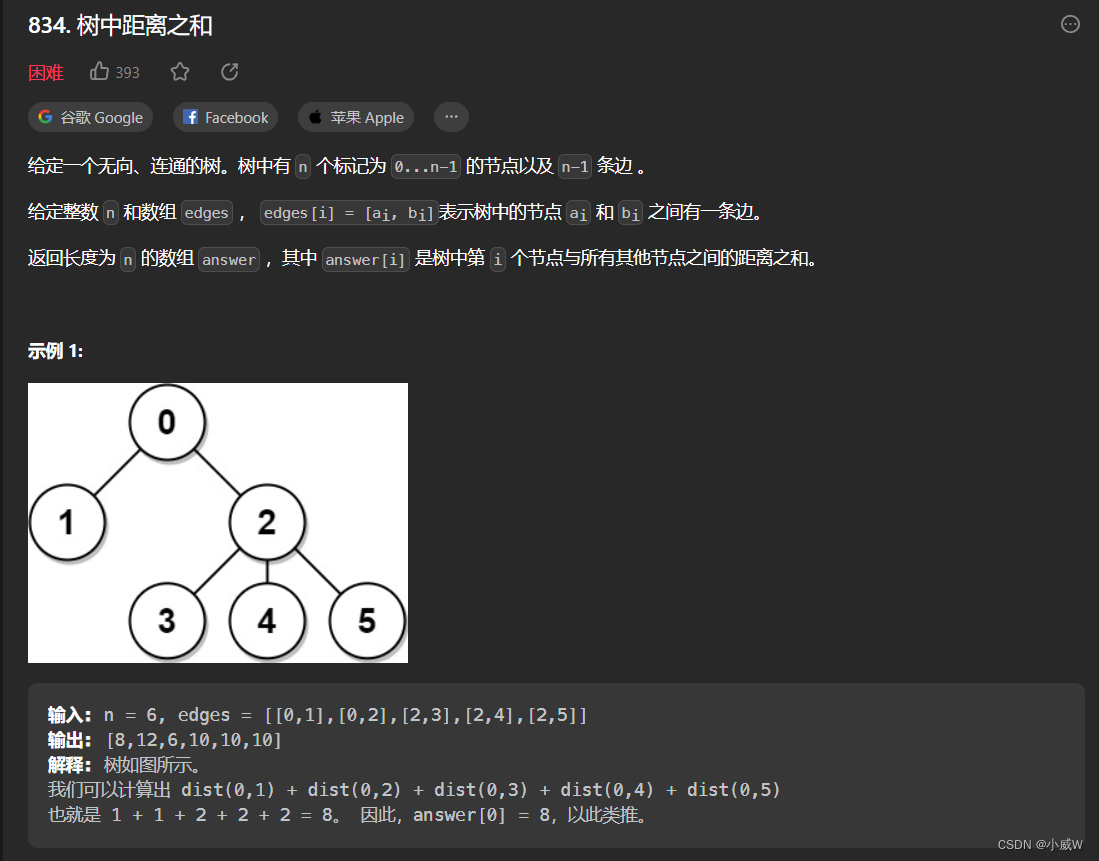
思路——冷静分析，列出式子

https://leetcode.cn/problems/sum-of-distances-in-tree/solutions/103325/c-liang-ci-dfsde-dao-da-an-by-congwang357-2/

将问题拆分：对于两个相邻节点A和B，将树拆分为两个子树，根节点分别为A和B，A节点到其他所有节点的距离和 ans(A) = A子树中所有节点到A节点的距离和sum(A) + B子树中所有节点到B节点的距离和sum(B) + B子树的大小cnt(B);
同理，ans(B) = sum(B) + sum(A) + cnt(A);

由此我们得到： ans(A) = sum(A) + sum(B) + cnt(B); ans(B) = sum(B) + sum(A) + cnt(A);
则，两个相邻接点的解之间的关系为：ans(A) = ans(B) - cnt(A) + cnt(B) = ans(B) - cnt(A) + (N - cnt(A));

因此，对于根节点root的任意子节点child，ans(child) = ans(root) - cnt(child) + N - cnt(child);

class Solution {
    List<Integer>[] g;
    int[] ans, size;    // size是各个节点作为根节点的子树大小
    int n;
    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<Integer>());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        this.n = n;
        ans = new int[n];
        size = new int[n];
        Arrays.fill(size, 1);

        dfs(0, -1, 0);
        reroot(0, -1);
        return ans;
    }

    // 求ans[0]和各个size[i]
    void dfs(int x, int fa, int depth) {
        ans[0] += depth;                    // depth 是 0 到 x 的距离
        for (int y: g[x]) {
            if (y != fa) {
                dfs(y, x, depth + 1);
                size[x] += size[y];         // 累加 x 的儿子 y 的子树大小
            }
        }
    }

    // 求答案
    void reroot(int x, int fa) {
        for (int y: g[x]) {
            if (y != fa) {
                ans[y] = ans[x] + n - 2 * size[y];
                reroot(y, x);
            }
        }
    }
}

算法分析⭐⭐⭐⭐⭐

https://leetcode.cn/problems/sum-of-distances-in-tree/solutions/2345592/tu-jie-yi-zhang-tu-miao-dong-huan-gen-dp-6bgb/

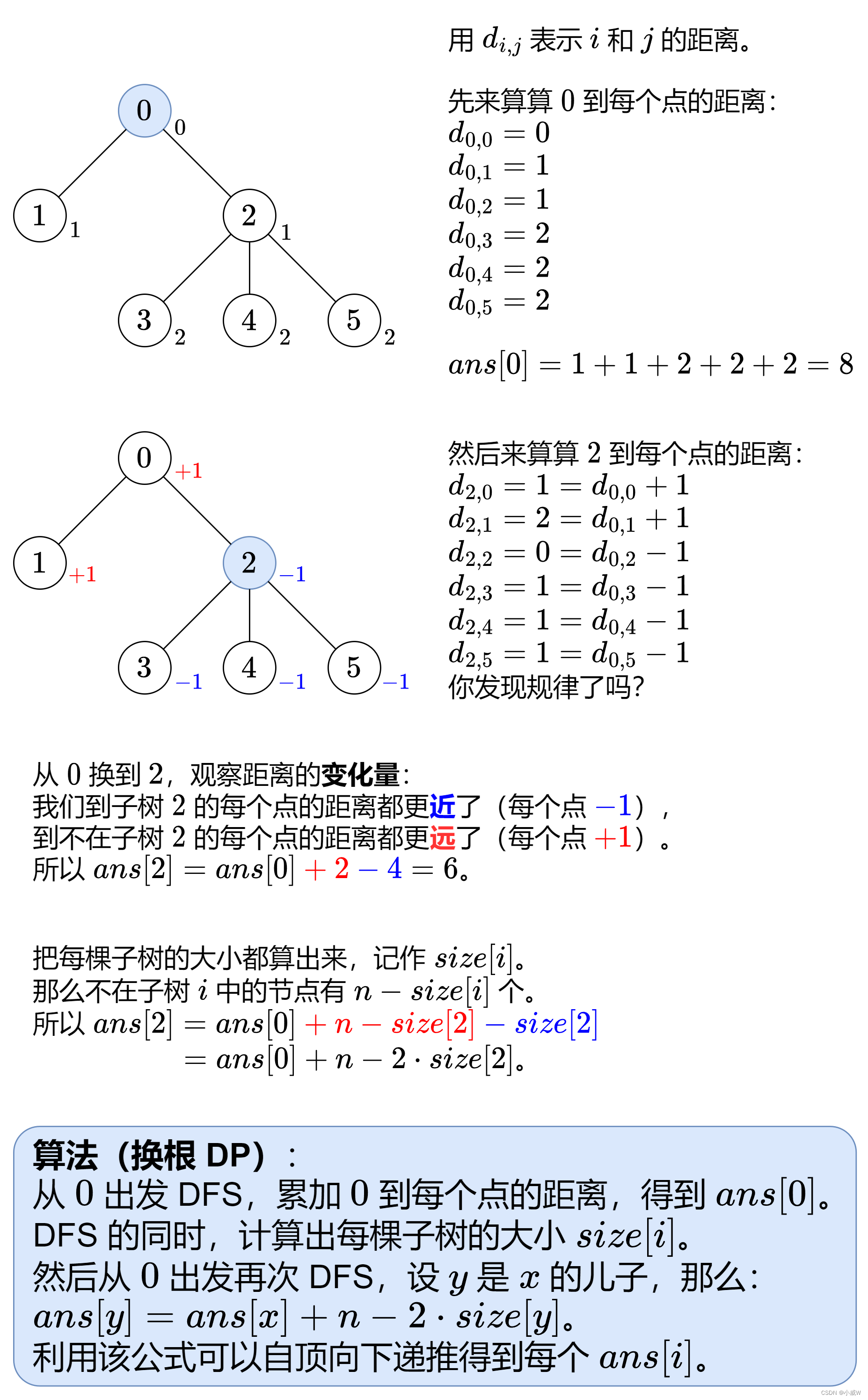
我们得到了重要公式：
$ans[y]=ans[x]+n-2\ast size[y]$

如何理解？
y 和以 y为根的子树的距离相比 x 与 以 y为根的子树的距离 少了 cnt[y]
除了 以 y为根的子树，剩下的节点数量是 n - cnt[y]，这些和 y 的距离相比 和 x 的距离多了 n - cnt[y]

因此：ans[y] = ans[x] + n - 2 * size[y]

补充：相关题目列表（换根DP）🐂！

更多题目参见：【算法】换根DP