匈牙利算法解决英雄配色问题
最近在开发中遇到了这种情况,策划要为每个英雄去做配色,一个英雄在表中可能有多个配色(可能重复),每次对局要选出五个英雄并让他们的颜色不同
(实际不是这个,简化成的这个需求)
第一反应应该用图去做,想到是递归、回溯
匈牙利算法
匈牙利算法是一种经典的图论算法,用于解决二分图最大匹配问题。匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于1955年提出该算法。此算法之所以被称作匈牙利算法,是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
在正式了解匈牙利算法之前,我们必须先知道什么是二分图:又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
如图所示
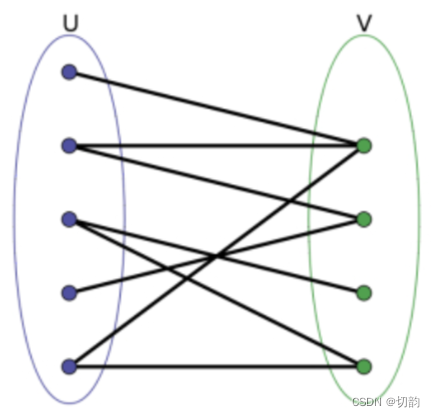
这就是一个典型的二分图,我们区别二分图,通常要看它是否能分成两个独立的点集。二分图是这样一个图: 有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中,每个顶点集中没有边直接相连接
在图论中,一个匹配是一个边的集合其中任意两条边没有公共顶点。
每一条线都代表该英雄可能有的配色
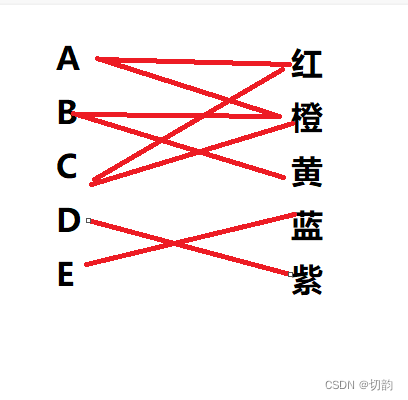
按照策划的要求应该变成这样
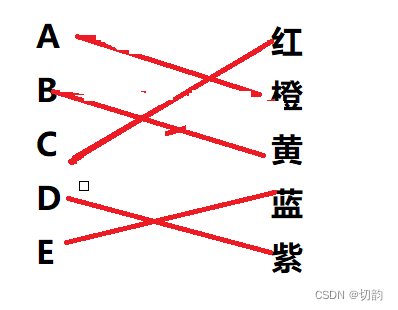
最大匹配:选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)
完美匹配:如果一个匹配中,图中的每个顶点都和图中某条边相关联,则此匹配称为完美匹配。
我们的问题就是找最大匹配,借助的就是匈牙利算法,(当配色无法满足时可能需要加上临时配色,这个需要后续沟通)
该算法的核心就是寻找增广路径,用增广路径来求二分图的最大匹配的算法。
增广路径
增广路径(Augmenting Path)是匈牙利算法中的一个重要概念。它在寻找二分图最大匹配的过程中起到关键作用。
在匈牙利算法中,增广路径是指从一个未匹配的顶点开始,经过一系列交替的匹配边和非匹配边,最终到达另一个未匹配的顶点的路径。增广路径的特点是它的起点和终点都是未匹配的顶点。
匈牙利算法通过不断寻找增广路径来增加匹配的数量。具体步骤如下:
选择一个未匹配的顶点作为起始点。
尝试将起始点与其相邻的未匹配顶点进行匹配。
如果存在增广路径,则通过交替改变匹配和非匹配边的状态,增加匹配的数量。
重复步骤2和步骤3,直到无法找到增广路径为止,即找到了最大匹配。
增广路径的寻找可以使用深度优先搜索(DFS)或广度优先搜索(BFS)等方法。在每次寻找增广路径时,算法会记录访问过的顶点,以避免重复访问,从而提高效率。
通过不断寻找增广路径并更新匹配,匈牙利算法可以找到二分图的最大匹配。
总结来说,增广路径是匈牙利算法中用于增加匹配数量的关键概念。它是从一个未匹配的顶点开始,通过交替的匹配和非匹配边构成的路径,最终到达另一个未匹配的顶点。匈牙利算法通过不断寻找增广路径来增加匹配的数量,从而求解二分图的最大匹配问题。
以上就是思路,下边是关键代码
一些变量
hero color两个table
bool line[maxn][maxn];//用邻接矩阵来存储hero和color的关系,行代表hero,列代表color,有则为true,无则false。
bool used[maxn];//判断颜色是否被使用。true则有,false则无。
int nex[maxn]//挪位置的
关键就是Find()方法,如何发现可以配对,则就有很多要点了,我们通过上述可知,若没有被使用,我们则可以直接使用,但我们判断颜色可不仅仅只是根据used来判断的,还有就是nex[]或者根据递归来腾位置,判断可不可以腾位置。
function Find(heroID)
for i = 1, #color do -- 遍历颜色
if line[heroID][i] and not used[i] then -- 如果可以使用该颜色且该颜色没有被使用
used[i] = true -- 我们则让它被使用
if nex[i] == 0 or Find(nex[i]) then
nex[i] = heroID -- 保存与该颜色配对的hero序号
return true -- 配对成功
end
end
end
return false -- 配对失败
end
然后就根据该方法计算match数,为五个就可以去把匹配数组的数据取出来,返回掉,不为五个就可能需要临时颜色补充一下。
需要将hero\color数据转换成类似邻接矩阵的形式(对数据进行处理)等着策划配表吧qwq