前言:在网上看了许多篇关于不同进制之间如何转换的文章,包括很多浏览量上万的博客。大多都只是把转换的规则罗列了出来,例如十进制转二进制,可能大家都知道方法,“除以2反向取余数,直到商为0”。应用该方法的确可以解决我们遇到的进制转换问题,但是如果问我们为什么这样做呢?可能很少有人可以回答的出来。另外,二进制、八进制、十进制、十六进制之间的转换规则有一大堆,当时费很大力气记住的规则,一段时间不使用,很容易就忘记了。于是,又从头到尾看了一遍原来的文章,不断的反复这个过程,浪费了很多时间和精力。根本原因是我们不了解底层的原理,当我们了解了底层原理之后,上述进制之间的转换规则完全可以自己推导出来,根本不用死记硬背。授人以渔,不如授人以渔。解决基本的进制转换问题,可以说看本篇文章就足够了。
进制转换
- 一、预备知识
- 二、其他进制转为十进制
- 三、十进制转化为其他进制
- 1、 整数部分的转化
- 2、小数部分的转换
- 四、二进制和八进制、十六进制之间的转化
- 1. 二进制转化为八进制、十六进制
- 2. 八进制、十六进制转化为二进制
一、预备知识
希望读者可以认真阅读本部分内容,因为后文进制转换的原理会以此部分内容为基础
以十进制数“1234”为例:
数码:就是数中每一位的数字。如1、2、3、4
数位:数码在这个数中的位置,从右到左从0开始递增。例如4的数位为0、3的数位为1
基数:就是每一位的数码可以有多少个数字来表示。其实就是所谓的进制,十进制,基数为十,数码可以取的值有10个,分别是0~9。
位权:对于多数位,处在某一位上的“1”所表示的数值的大小,称为该位的位权。例如十进制数位0,位权为 10^0 = 1,数位1,位权10^1 = 10,…, 数位为n,位权为10^n 。公式为 基数的数位次幂
补充说明,如果包含小数部分,小数点后的第一个数的数位为-1,小数点后的第二个数的数位为-2,以此类堆。
二、其他进制转为十进制
我们先从最简单的情况,转换为十进制开始介绍。对于数字11,它可能是二进制,也可能是八进制,还有可能是十进制、十六进制,为了避免产生歧义,我们统一使用在不同数字后添加不同符号字母的方式来表示不同进制的数。
不同进制所使用相应对后缀如下所示:
- B, Binary (二进制)
- O,Octal (八进制)
- D,Decimal (十进制)
- H,Hexadecimal (十六进制)
使用了对应单词的首字母,另外,注意八进制使用字母O表示,不要和数字0混淆。
不同进制转换为十进制的规则
数码 * 基数^数位
上文有提及到,* 表示乘法运算。^表示幂运算,即基数的数位次方。基数的数位次方,就是该位的位权,然后数码乘以该位的位权就是该位数值实际表示的数的大小。
我们以1010.101B、68O、A6H转化十进制为例
1010B (基数:2,数位从右向左,从0开始)
1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 10.625D
68O (基数:8)
6 * 81 + 8 * 8 0 = 48 + 8 = 56D
A6H (基数:16)
A * 161 + 6 * 160 = 10 * 16 + 6 = 166
应该很容易理解吧,任何进制转为十进制都是依据此方法计算。例如,你可以尝试算下四进制数11,七进制数11分别表示的十进制是多少?答案在评论区。
三、十进制转化为其他进制
由于整数部分和小数部分的处理方式是不同的,因此我们将分为两部分介绍。主要以二进制为例展开讲解。
1、 整数部分的转化
十进制转化为二进制的规则为什么是除以2反向取余数,直到商为0?
如下图所示:

1除以2时不够除,商为0余数为1
我将10D和展开后的1010B二进制数同时除以2,二进制数每一位的权重都减少了1,但是最后一位(最右边的一位),其数位为0无法在减少了(假如减1,那么数位就是-1,就成为小数点后一位了,然而我们想得到余数,并不想让结果为小数),余数就是最后一位的数码。
当一个某进制的整数除以该数的基数,得到的余数就是数位为0(最低位或最后一位)的数码。
本部分内容相当重要,十进制转换为其他进制的核心,所以我要尽可能详细的说明。
为了方便理解,我们以十进制数1234为例
十进制数,基数为10
1234 = 1 * 103 + 2 * 102 + 3 * 101 + 4 * 100
两边同时除以基数10
1234 / 10 = 123 … 4
1 * 102 + 2 * 101 + 3 * 100 4 * 100
从1234的角度看4除以10不够了,所以余数4从展开式的角度看,其他数位都可以减一,但是最后一位的数位是0,无法减一了,所以余数4 * 100 = 4,或者认为是权重为104的系数4
也就验证了上面那句话,十进制数1234除以基数10,得到的余数就是(原数1234)数位为0的数码4。(内心OS:我个人觉得术语余数使用于展开式中,术语数位和数码适用于原数本身。)
对于123,进行递归运算就好了,十进制数123除以基数10,得到的余数就是(原数123)数位为0的数码3,同时也是(原数1234)数位为1(倒数第二位)的数码3。
回到最初的问题,十进制转化为二进制的规则为什么是除以2反向取余数,直到商为0?
现在可以解答了,
除以2是因为我们要转化为二进制数,二进制数的基数是2,
反向取余数,因为每次得到的余数其实是要转换为的二进制数的
最低的数码,换句话说最先得到的余数是最低位的数码,最后得到的余数是最高位的数码,所以要反向取余数
不知道我讲明白了没有,如果有问题欢迎评论区提出来,我很希望把这部分内容讲解清楚。
2、小数部分的转换
十进制小数转化为二进制小数的规则为什么是乘以2取整,正向取整数?
如下图所示:

我们将0.625D和0.101B的展开式同时乘以2,二进制数的每一位权重都增加了1,原来的最高位的数位从-1变为了0,换句话说,该数码从小数部分的最高位变为了整数部分的最低位,该数码已经不属于小数部分了。效果好像是小数点向右移动了一位。
当一个某进制的小数乘以该数的基数,得到的整数部分的值(数位为0的数码)就是小数部分数位为-1(小数部分最高位)的数码。其效果等同于小数点向右边移动一位
为了方便理解,我们以十进制小数0.123为例
0.123 = 1 * 10-1 + 2 * 10 -2 + 3 * 10-3
两边同时乘以基数10
1.23 = 1 * 100 + 2 * 10 -1 + 3 * 10-2
从1.23角度看,乘以10后的整数部分,就是原来小数的最高位
从展开式角度看,所有数位都增加了1,原来小数的最高位,已经成为了整数的最低位,已经不是小数部分的数码了。 数位为0的数码就是小数部分数位为-1(小数部分的最高位的数码),此时数位为0的数码是1,所以小数数位的最高位为1
或者简单的理解方式,一个小数乘以该数的基数相当于小数点向右移动一位,那么得到的整数的最低位自然就是原来小数的最高位
让我们回到最初的问题:十进制小数转化为二进制小数的规则为什么是乘以2取整,正向按顺序取整数?
乘以2是因为2是二进制的基数,(相当于小数点向右移动一位)
正向按顺序取整是因为,乘以2得到的第一个整数是原来小数的最高位,得到的第二个整数时原来小数的第二最高位。可以想想小数点一步步向右移动,每次得到的都是新小数的最高位。
对于其他进制处理方式和二进制相同,乘以基数按顺序取整。
至此,我们学习了其他进制转化位十进制和十进制转化为其他进制的规则。这里做一个小总结:
其它进制转化为十进制
数码 * 基数^数位
十进制转化为其他进制
整数部分处理
当一个某进制的整数除以该数的基数,得到的余数就是数位为0(最低位或最后一位)的数码。
小数部分处理
当一个某进制的小数乘以该数的基数,得到的整数部分的值(数位为0的数码)就是小数部分数位为-1(小数部分最高位或第一位)的数码。
换个思路,一个某进制的小数乘以该数的基数,其效果等同于小数点向右边移动一位,得到的整数部分的最低为数码自然是原小数部分最高位的数码。
其实到这里就可以实现任意两个进制之间的转换了,思路是通过十进制这座桥梁,先把待转换进制转化为十进制,在把十进制转化为最终的目标进制。
不过,二进制和八进制、二进制和十六进制之间的转换还存在更简单的方式,因此我们下文继续来介绍。
四、二进制和八进制、十六进制之间的转化
1. 二进制转化为八进制、十六进制
我依然想用“展开式”的方式,来建立二进制和八进制以及二进制和十六进制之间的联系,
10000B = 20O = 10H
1*24 + 0 * 23 + 0 * 22 + 0 * 21 + 0 * 20
2 * 82 + 0 * 80
1 * 161 + 0 * 160
似乎无法找出它们在数学上的联系。获取是我数学水平没有达到,如果有哪位大佬可以看出来可以在评论区留言,不过我想尝试利用本文的预备知识来给出一个相对看似合理的解释。可以重新回顾下预备知识如果忘记了。
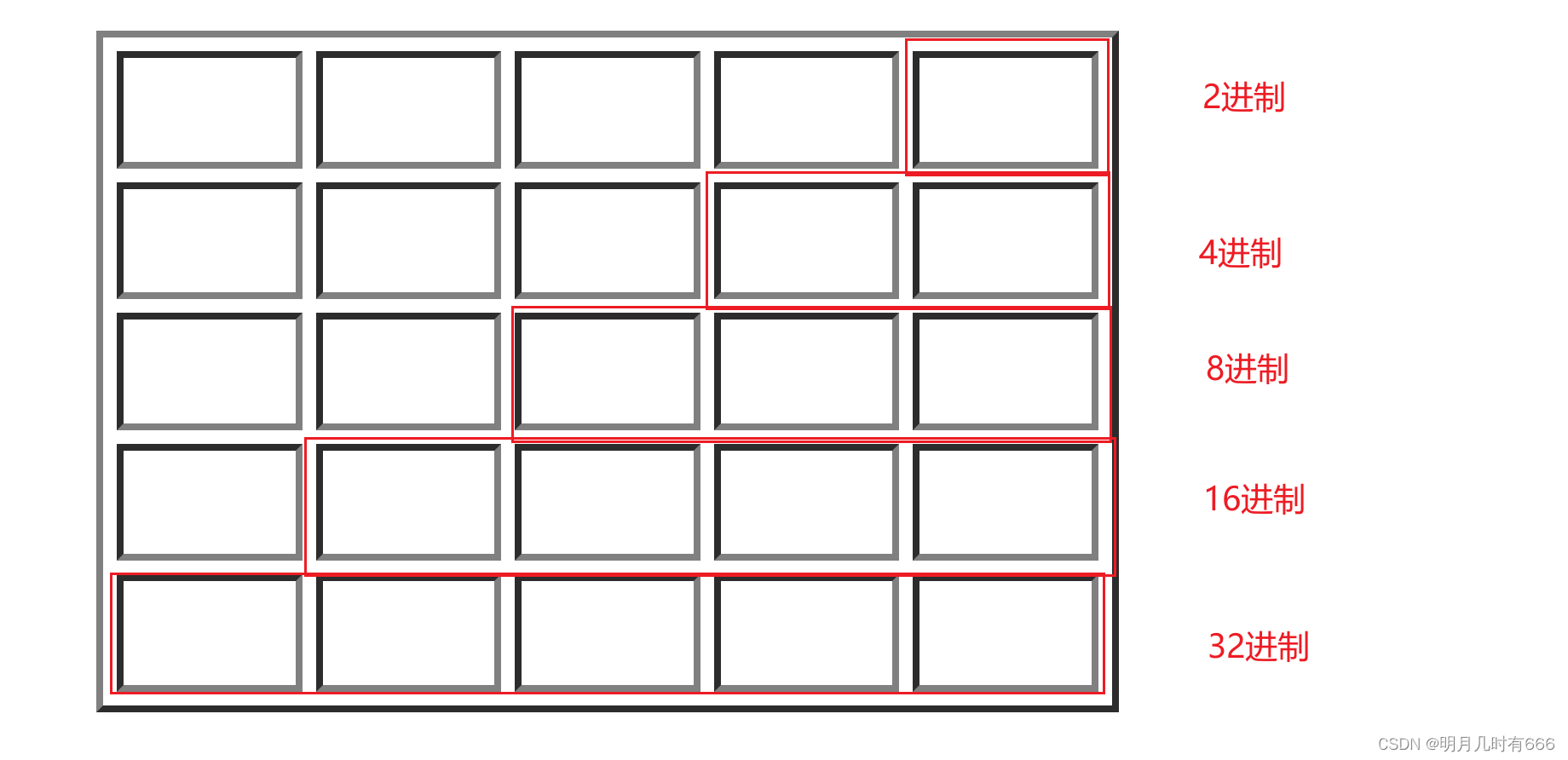
如图所示,一个方格表示一个二进制位,把单独一个小格看成一个整体,其能表示两种状态,换句话说,每一个位可以有两个数字来表示,所以是二进制数。
把连续的两个方格看成一个整体,其可以表示四种状态,换句话说,每一位可以有四个数字来表示,所以相当于四进制数。
把连续的三个方格看成一个整体,其可以表示8种状态,换句化说,每一个位可以有八个数字表示,所以相当于8进制。
其它略。
我们以8进制为例,
其每一个的数码包括{0, 1 , 2, 3, 4, 5, 6, 7} ,其本质就是8种连续的状态而已,我们可以使用三位二进制来表示这八种状态{000, 001, 010, 011, 100, 101, 110, 111}
10000B = 20O = 10H

2. 八进制、十六进制转化为二进制
和一中描述的过程相反,每一个独立的八进制数、十六进制数转化为相应的二进制数。