A - Together

题目描述

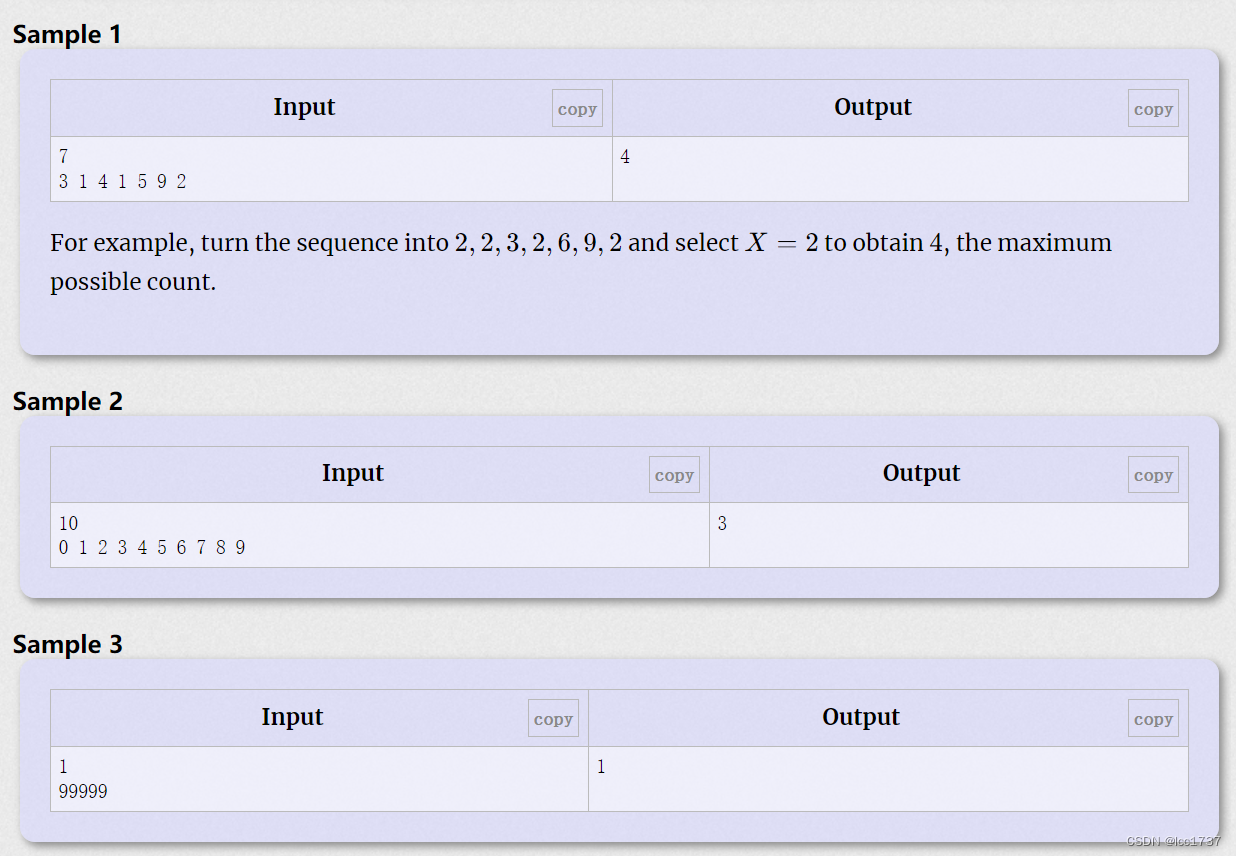
题意分析

题意：给出n个数，可以对每一个数做三种操作a，a+1,a-1，求所有操作完成后出现次数最多的数的个数。

分析：对于每个数枚举三种操作后的值，记录其出现次数，最后遍历求出现次数的最大值


解题思路


对于每个数都有三种操作方式，我们只需将每个数都进行三次操作，并统计操作后的数出现的次数，最终选出最大出现次数的那个数即可


复杂度分析


这个解法的时间复杂度是 O(N)。

主要的操作有:

1. 读取 N 个输入数字,复杂度 O(N)
2. 对每个数字 num[x]、num[x-1]、num[x+1] 加 1,复杂度 O(3N) = O(N)
3. 遍历 num 数组找到最大值,复杂度 O(N)

所以总的时间复杂度是 O(N) + O(N) + O(N) = O(N)。
空间复杂度是 O(N),因为使用了大小为 N 的 num 数组来统计次数。


带注释的代码

#include<iostream>
#include<vector>
using namespace std;
typedef long long ll; 
const int N=1e5+5;
int num[N]={0}; //数组较大的时候用全局变量 
 
int main(){
	int n,x; //n为几个数 
	cin>>n;
	vector<int> a(n); //动态数组 
	for(int i=0;i<n;i++){ //统计每个数不变，加一，减一分别出现的次数 
		cin>>x;
		num[x]++; 
		num[x-1]++;
		num[x+1]++;		
	}
	int zc=INT_MIN; //最小整数 
	for(int i=0;i<N;i++)
	{
		zc=max(zc,num[i]); //求出最大出现次数的那个数 
	}
	cout<<zc;
}

B - Fractions Again?

题意分析


题意：对于输入的值k，给出所有满足1/k=1/x+1/y的结果

分析：遍历x求y，记录所有满足的结果


解题思路


首先我们将等式变形一下

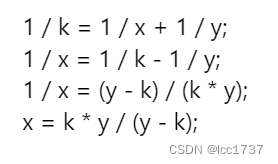
可以发现我们需要让ky整除y-k，同时我们发现y是从k+1开始遍历，同时当x=y的时候，y的值最大到2k，以此确定了y的上限

复杂度分析

外层while循环：表示持续输入k。循环的次数取决于输入的k的个数。

时间复杂度：O(N)，N为输入的k的个数。

内层for循环：循环从k+1到2k，寻找满足条件的整数对。

时间复杂度：O(k)。

内层for循环：输出所有满足条件的整数对。

时间复杂度：O(t1)，t1为满足条件的整数对的个数。

综上所述，代码的总体时间复杂度为O(N * k * t1)，其中N为输入的k的个数，t1为满足条件的整数对的个数。空间复杂度主要由a和b的空间占用决定，为O(t1)。


带注释的代码

#include<bits/stdc++.h>
using namespace std;
int main(){
	int k;
	while(cin>>k){ //持续输入k 
		int t1=0; //记录有几组数据 
		vector<int> a(1005); //用来存x 
		vector<int> b(1005); //用来存y 
		for(int y=k+1;y<=2*k;y++) //y从k+1开始,最大到2*k 
		{
			if((k*y)%(y-k)==0) //如果可以整除,说明x为整数 
			{
				if(k*y/(y-k)>=y) //如果x>=y 
				{
					a[t1]=k*y/(y-k); //存x 
					b[t1]=y; //存y 
					t1++; //组数加1 
				}
			}	
		}
		cout<<t1<<endl; //存组数 
		for(int i=0;i<t1;i++)
		{ 
			printf("1/%d = 1/%d + 1/%d\n",k,a[i],b[i]); //按照格式输出 
		}
	}
}