F-全体集合_牛客小白月赛43 (nowcoder.com)

题意：

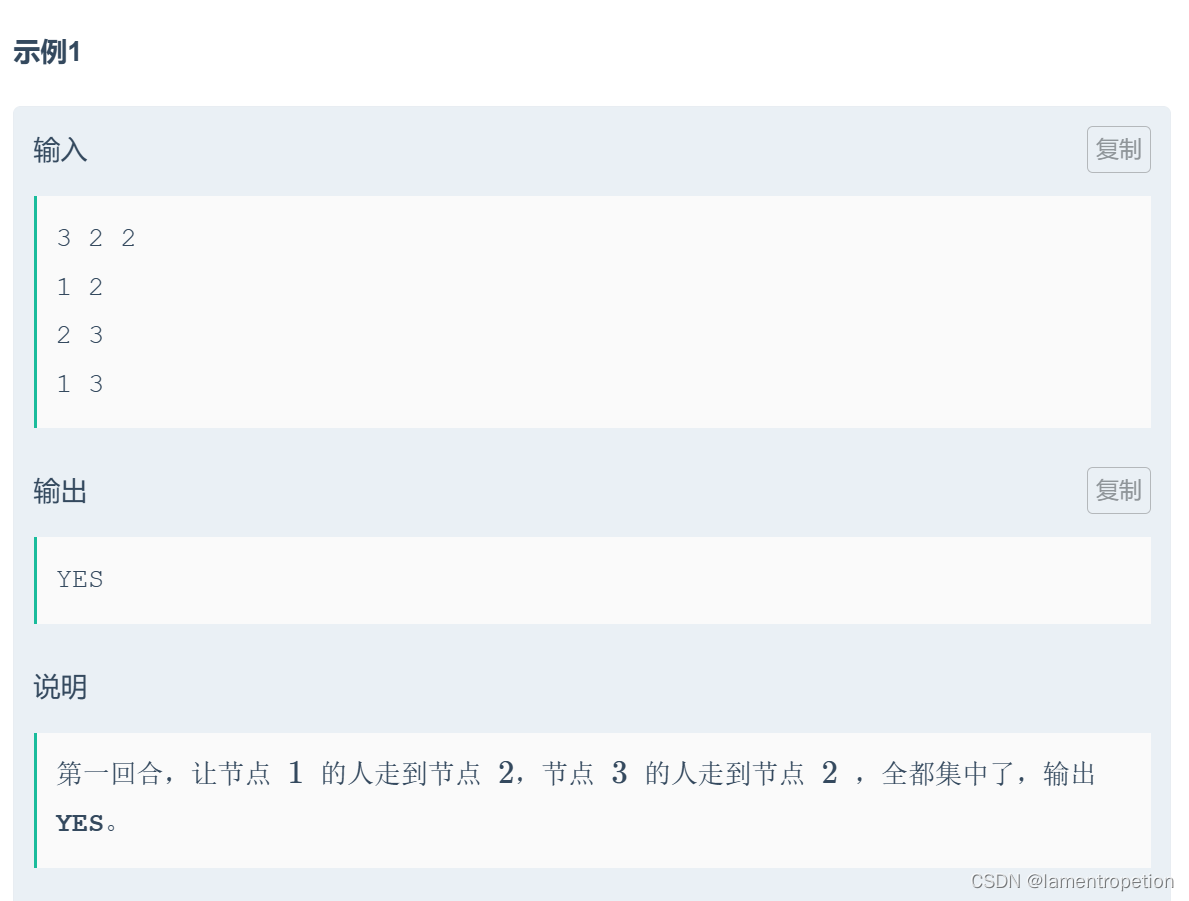
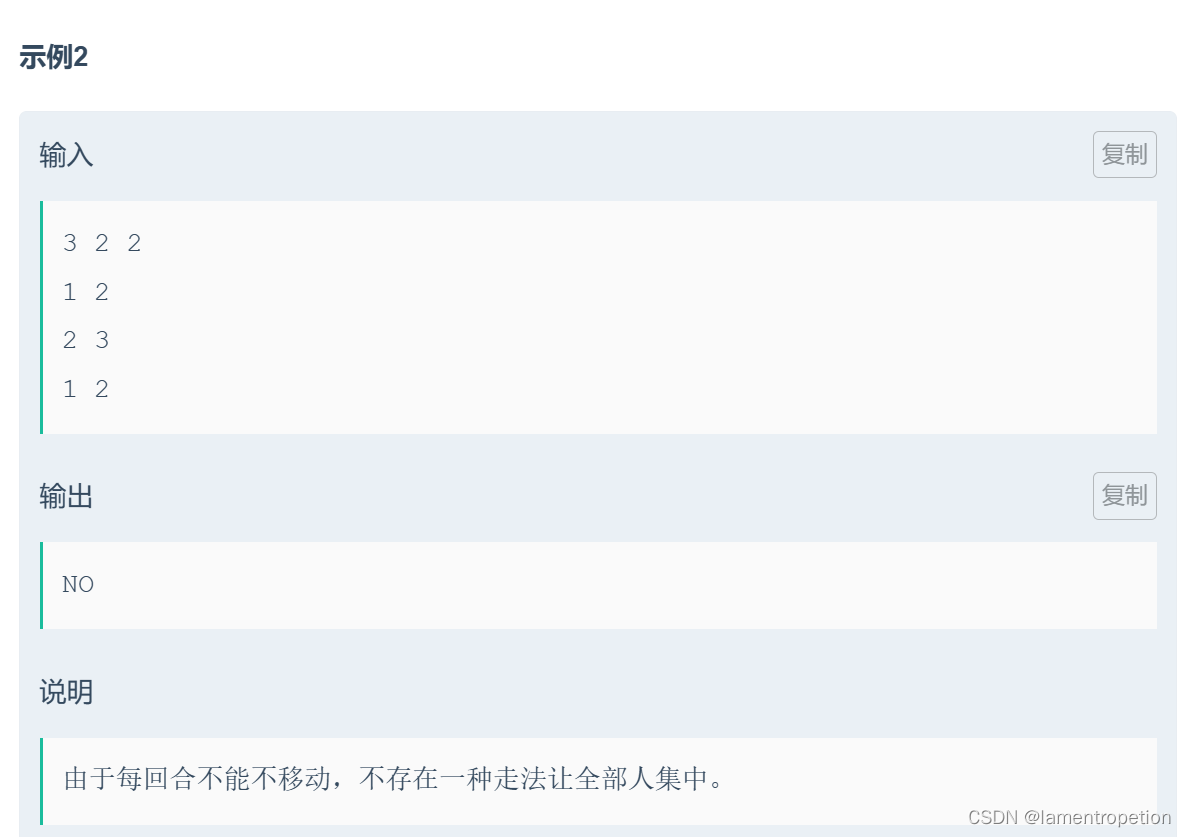
思路：

首先是经典的猜结论环节

这个结论可以想象特殊情况，把图看成一条链，多模拟几个例子

然后会发现一个很显然的结论：在链上的两个人点之间的距离一定是偶数

然后把结论进行推广到树，即对于一棵树用这个结论，发现树上任意两点之间距离一定是偶数

推广到图上也一样

这是图论的一种很重要的思考方式，即从链思考性质，然后试图推广到树（两条链合并到一起），然后是图（加上环）（中间也可以尝试基环树）

然后有个很重要的一点，如果图上两个点之间存在奇环，那么这两个点之间距离的奇偶性可以改变，否则不能改变

图上两个点之间距离的奇偶性和奇环有关

做法二和分层图是一个道理

Code:

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=2e5+10;
const int mxe=5e5+10;

struct ty{
    int to,next;
}edge[mxe<<2];

queue<pair<int,int> > Q;

int N,M,K,u,v;
int tot=0;
int a[mxn];
int head[mxn];
int dis[mxn][2];

void add(int u,int v){
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void G_init(){
    tot=0;
    for(int i=0;i<=N;i++){
        head[i]=-1;
    }
}
void bfs(){
    Q.push({a[1],0});
    dis[a[1]][0]=1;
    while(!Q.empty()){
        auto u=Q.front();
        Q.pop();
        for(int i=head[u.first];~i;i=edge[i].next){
            if(dis[edge[i].to][u.second^1]) continue;
            dis[edge[i].to][u.second^1]=1;
            Q.push({edge[i].to,u.second^1});
        }
    }
}
void solve(){
    cin>>N>>M>>K;
    G_init();
    for(int i=1;i<=M;i++){
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    for(int i=1;i<=K;i++) cin>>a[i];
    bfs();
    for(int i=1;i<=K;i++){
        if(!dis[a[i]][0]){
            cout<<"NO"<<'\n';
            return;
        }
    }
    cout<<"YES"<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}