目录

​编辑

一，交换排序算法的简介

二，冒泡排序

冒泡排序代码：排升序

三，快速排序

1.霍尔大佬写的快速排序

2.挖坑法

3.前后指针法

四，以上代码的缺陷与改正方法

三数取中

三路划分：

五，随机数取中

六，快速排序的非递归

---

 

一，交换排序算法的简介

交换排序，顾名思义便可以知道这是一种通过交换来实现排序的算法。在这这种算法中有一种最简单最好理解的算法叫做冒泡排序。但是这种算法的效率十分低下，在现实生活中不足为用。还有一种算法叫做快速排序，这种算法的效率很高被广泛应用。并且，这种算法有许多个版本。

二，冒泡排序

虽然冒泡排序效率十分低下，但是我仍然要介绍一下这种算法。这种算法的精华一句话便可以总结出来：相邻的两两比较，遇到不相等的便交换。

冒泡排序代码：排升序

void swap(int* p, int* q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;
}
void BubbleSort(int* a, int n)
{
	int flag =1;
	for (int i = 0;i < n;i++)
	{
		for (int j = 0;j < n-i-1;j++)
		{
			if (a[j] > a[j+1])
			{
				swap(&a[j], &a[j+1]);
				flag = 0;
			}
		}
		if (flag)
		{
			break;
		}
	}
}

三，快速排序

快速排序，虽然与冒泡排序同样是交换排序算法的一种但这种排序算法却比冒泡排序的效率快的多。并且快速排序的写法也有三种：

1.霍尔大佬写的快速排序

2.挖坑法

3.指针法
 下面我就来对这三种快速排序的写法进行一一介绍。

1.霍尔大佬写的快速排序

代码：

int PartSort1(int* a, int left, int right)
{
	int keyi = left;//将数组的第一个数据作为关键值
	while (left < right)
	{
		while (right > left && a[right] >= a[keyi])//右边找小于关键值的元素
		{
			right--;
		}
		while (right > left && a[left]<= a[keyi])//左边找大于关键值的元素
		{
			left++;
		}
		swap(&a[left], &a[right]);//找到后交换左右的值让小的在右边，大的在左边
	}
	swap(&a[keyi], &a[left]);//循环结束后，left与right是相交的，所以在这个相交的位置放上关键值再在关键值原来的位置上放上原相交位置上的值
	keyi = left;
	return keyi;//返回相遇位置
}
//递归调用
void QuickSort(int* a, int begin,int end)
{
	if (begin >= end)//当范围为0或范围不存在时便返回
	{
		return;
	}

	int keyi = PartSort1(a, begin, end);

	QuickSort(a ,begin, keyi - 1);//调整左区间
	QuickSort(a , keyi + 1, end);//调整右区间

}

霍尔大佬写的快速排序可能就是第一代快速排序算法了。这个排序算法的主要思想就是将比a[keyi]小的值放在左边，将比a[keyi]大的值放在右边。最后将左右指针相遇的位置与a[keyi]交换。

但是这个算法有几个坑：
1.一般我们在选keyi时选择的都是最左边或者最右边的值。在这里左右两个指针走的顺序就有讲究了：

1.当我们选择了最左边的值作为keyi时，我们就要让right先走，

当我们选择了最右边的值作为keyi时，我们就要让left先走。

2.left与right指针的指向也要保证指向最左边或者最右边的值，否则就会发生错误。

2.挖坑法

因为霍尔大佬写的代码有很多需要谨慎处理的地方，所以就有人写了一个对霍尔大佬的代码进行优化的算法——挖坑法。代码如下：

代码：

int PartSort2(int* a, int left, int right)
{
	int key = a[left];//记录关键值
	int hole = left;//初始化坑位
	while (left < right)
	{   //在右边找能够填坑的值并填坑
		while (left < right && a[right] >= key)
		{
			right--;
		}
		swap(&a[right], &a[hole]);
		hole = right;
		//在右边找能够填坑的值并填坑
		while (left < right && a[left] <= key)
		{
			left++;
		}
		swap(&a[hole], &a[left]);
		hole = left;
	}
   //找到最后一个坑，将关键值填入并返回关键值的下标
	swap(&a[hole], &a[left]);
	hole = left;
	return hole;
}
void QuickSort(int* a, int begin,int end)
{
	if (begin >= end)
	{
		return;
	}

	int keyi = PartSort2(a, begin, end);

	QuickSort(a ,begin, keyi - 1);
	QuickSort(a , keyi + 1, end);

}

这个算法便不再需要像霍尔大佬的算法一样顾虑那么多。但是这个算法的循环还是多了点。死循环的概率还是大了点。为了减少循环，又有人对这些代码进行优化。

3.前后指针法

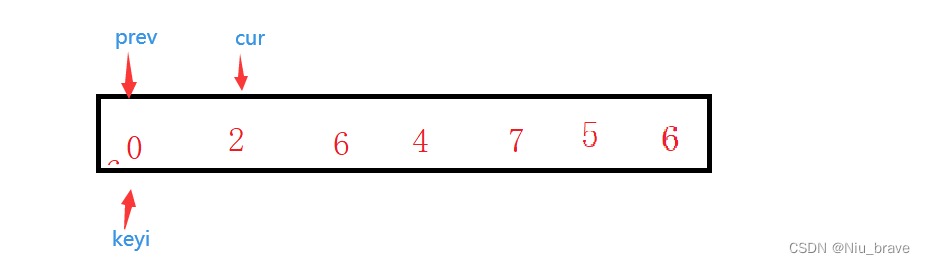
指针法可谓是这三种快速排序的写法中最简单的一种写法了。这个算法的大概思想如下：

1.用一个keyi记录最左边或者最右边的值的下标

2.再定义两个指针cur与prev。这两个指针的指向如下：

3.把cur当作一个探路者，cur无条件的向前冲。当cur感知到自己指向的数据比a[keyi]小的时候便停下来交换cur与++prev指向的数据。当cur大于右边的边界条件时便结束循环。

代码如下： 

代码：

int PartSort3(int* a, int left, int right)
{ 
    
    
	int keyi = left;
	int prev = left;
	int cur = left + 1;

	while (cur<=right)
	{   //这里的prev一定要先加加
		if (a[cur] <a[keyi]&&++prev!=cur)
		{
		
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}

	swap(&a[keyi], &a[prev]);
	keyi = prev;
	return keyi;
}
//递归调用
void QuickSort(int* a, int begin,int end)
{
	if (begin >= end)
	{
		return;
	}

	int keyi = PartSort3(a, begin, end);

	QuickSort(a , begin, keyi - 1);
	QuickSort(a , keyi + 1, end);

}

这个指针法便减少了代码内的循环可以大大的减少死循环的风险！！！

四，以上代码的缺陷与改正方法

虽然上面的代码可以很快的将一些数据进行排序，但是对于一些比较极端的场景下上面的代码排序起来就会变得十分吃力。比如：

1.当排序的数据是有序的数据时，上面的代码排序起来的时间复杂度就会是O(n2)

2.当排序的数据的量十分多，并且重复的数据也十分多时，上面的快速排序就会排不出来有栈溢出的风险。

针对上面的两个问题，可以给出下面的解决方案：

1.三数取中

2.三路划分

三数取中

三数取中针对的场景是数据有序时的场景，比如：

int main()
{   //创建一个有序的数组
	int N = 10000000;
	int* a = (int*)malloc(sizeof(int) * N);
	for (int i = 0;i < N;i++)
	{
		a[i] = i;
	}
	//计算排序时间
	int begin = clock();
	QuickSort(a, 0, N-1);
	int end = clock();
	printf("QuickSort:%d ", end - begin);
	return 0;
}

要排序这串数据在我的编译器上会崩掉，崩掉的原因是栈溢出。

现在来加一段三数取中代码：

//三数取中，就是在左，中，右三个数中取中间值
int GetMid(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[mid] < a[left])
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
		
	}
	else
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if(a[left]>a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
//加入三数取中操作的快速排序
int PartSort1(int* a, int left, int right)
{
    //取出中间值然后与最左边的值交换让keyi指向中间元素
	int mid = GetMid(a, left, right);
	swap(&a[left], &a[mid]);
	int keyi = left;
	while (left < right)
	{
		while (right > left && a[right] >= a[keyi])
		{
			right--;
		}
		while (right > left && a[left]<= a[keyi])
		{
			left++;
		}
		swap(&a[left], &a[right]);
	}
	swap(&a[keyi], &a[left]);
	keyi = left;
	return keyi;
}

效果：

虽然排起来并不算快，但是总算是排出来了。

三路划分：

 虽然上面的代码把有序的情况给排出来了，但是还有一种极端情况三数取中这个解决办法是解决不了的。那便是存在大量的重复元素的时候。比如：

int main()
{   //创建一个数据全是2的数组
	int N = 10000000;
	int* a = (int*)malloc(sizeof(int) * N);
	for (int i = 0;i < N;i++)
	{
		a[i] = 2;
	}
	//计算排序时间
	int begin = clock();
	QuickSort(a, 0, N - 1);
	int end = clock();
	printf("QuickSort:%d\n ", end - begin);
	return 0;
}

这个数组如果用三数取中的话是不可能取到中间数的，所以三数取中没有用。如果按照原代码那样写的话也会栈溢出。所以有大佬就想到了三路划分的解决方法。

三路划分：

这个方法的思想和这个方法的名字一样：

就是要将一组数据划分成三路：左路，中路，右路。当我们再次递归时只需要递归左路与右路。这样做便可以大大减少递归的深度，防止栈溢出。

实现思想：

1.定义三个指针：cur,left,right.同时用key记录a[left]的值。

2.当a[cur]小于key时便将a[cur]与a[left]交换，同时left++,cur++。

   当a[cur]大于key时便将a[cur]与a[right]交换，right--,cur不动。

   当a[cur]与key相等时，cur++，left与right不动。

3.当cur超过right时循环停止。

4.再次排序时排序的范围是：[begin,left-1],[right+1,end]

写成代码如下：

代码：

//三路划分
void QuickSort2(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
     }

	int left = begin;
	int right = end;
	int cur = begin + 1;
    
    //三数取中
	int midi = GetMid(a,left, right);
	swap(&a[left], &a[midi]);

    //三路划分，开始甩值到左右两边
	int key = a[left];
	while (cur <= right)
	{
		if (a[cur] < key)
		{
			swap(&a[cur], &a[left]);
			left++;
			cur++;
		}
		else if (a[cur] > key)
		{
			swap(&a[cur], &a[right]);
			right--;
		}
		else
		{
			cur++;
		}
	}
    
    //只递归两边的区间
	QuickSort2(a, begin, left - 1);
	QuickSort2(a, right + 1, end);
}

 这个代码便可以跑过有大量重复数据的数组排序，也能跑过有序的大量数据。

但是当我们要跑这个oj排序数组 时出现这种情况：

 虽然测试用例都过了，但还是没有将这道题通过，因为时间限制。

五，随机数取中

 为了通过这道OJ题，这里又得来上一个随机数取中的操作。因为在这道题的用例中可能存在着一些用例非常的接近导致取中的操作效率变低。所以为了提高效率，我们便可以采用随机数取中。

代码：

int GetMid(int* a, int left, int right)
{
    //只是改了这里
    srand(time(0));
	int mid = left+rand()%(right-left);
	if (a[mid] < a[left])
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
		
	}
	else
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if(a[left]>a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

结果：

 过啦！！！

六，快速排序的非递归

 前面我们写的快速排序都是递归版本的。递归版本的代码虽然简单但是递归调用的栈空间却比较小，很容易就会栈溢出。所以为了避免栈溢出的风险，我们便要实现一个非递归版本的快速排序算法。这个非递归写法的快速排序要用到一个数据结构就叫作栈（这个栈是我们定义的，这是一个堆上的栈）。非递归版本代码如下：

代码：

void QuickSortNR(int* a, int begin, int end)
{   //定义栈并初始化栈
	Stack stack;
	StackInit(&stack);
    //在栈中插入begin和end这个区间，牢记栈后进先出的特点。
	StackPush(&stack, end);
	StackPush(&stack, begin);

	while (!StackEmpty(&stack))
	{
        
		int left = StackTop(&stack);
		StackPop(&stack);
		int right = StackTop(&stack);
		StackPop(&stack);
        //根据区间排序
		int keyi = PartSort1(a, left, right);
        
        //判断区间是否存在再插入区间（先右后左，因为栈的特点是后进先出）
		if (keyi + 1 < right)
		{
			StackPush(&stack, right);
			StackPush(&stack, keyi + 1);
		}
		if (keyi - 1 > left)
		{
			StackPush(&stack, keyi - 1);
			StackPush(&stack,left);
		}
	}
    //栈销毁
	StackDestroy(&stack);

}

快速排序的非递归版本需要使用到数据结构中的栈，所以为了实现非递归版本的快速排序我们就得自己定义一个栈。这个栈的作用就是用来分割排序区间的。