给定一个无向、连通的树。树中有 n 个标记为 0…n-1 的节点以及 n-1 条边 。
给定整数 n 和数组 edges , edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。
返回长度为 n 的数组 answer ,其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。
示例 1:
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此,answer[0] = 8,以此类推。
示例 2:
输入: n = 1, edges = []
输出: [0]
示例 3:
输入: n = 2, edges = [[1,0]]
输出: [1,1]
提示:
1 <= n <= 3 * 104
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
给定的输入保证为有效的树
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/sum-of-distances-in-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题意:
首先给出节点数,然后给出有哪些边,最终的返回值是一个数组,ans[i]表示节点 i 到每一个节点的距离和。
思路:
树形DP。
首先是暴力的思路。
以根节点为例,定义 dp[u] 表示以 u 为根的子树,它的所有子节点到它的距离之和,同时定义 sz[u] 表示以 u 为根的子树的节点数量,不难得出如下的转移方程:
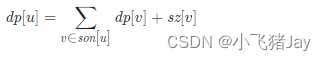
ok,那暴力的思路就是,把每个点都当作根结点,都跑一遍这样的代码,最终得到每个点的答案。
有更优化的思路嘛?
有的,只是我想不到而已。
跟之前一样,首先从 0 出发DFS , 累加 0 到每个点的距离,得到ans[0]。
在DFS的同时,计算出每棵子树dp值和sz值。
然后从 0 出发再次DFS , 这次就要得到剩下的所有节点的ans值。怎么得到呢?
假设 v 是 u 的子节点,那就有:
dp[u] -= dp[v] + sz[v];
sz[u] -= sz[v];
dp[v] += dp[u] + sz[u];
sz[v] += sz[u];
这是因为,当你把v看作父结点,u看作v的子节点的时候,v 不在 u 的后代集合中了,因此此时 dp[u] 需要减去 v 的贡献,同时sz[u]也要减去相应的sz[v]。
dp[u] -= dp[v] + sz[v];
而 v 的后代节点集合中多出了 u,因此 dp[v] 的值要由 u 更新上来,即:
dp[v] += dp[u] + sz[u];
同时 sz[v] 也要相应加上 sz[u]。
代码:
class Solution {
public:
vector<int> ans , sz , dp;
vector<vector<int>> graph;
void dfs(int u , int f){
sz[u] = 1;
dp[u] = 0;
for(auto& v:graph[u]){
if(v == f)
continue;
dfs(v,u);
dp[u] += dp[v] + sz[v];
sz[u] += sz[v];
}
}
void dfs2(int u , int f){
ans[u] = dp[u];
for(auto& v:graph[u]){
if(v == f)
continue;
int pu = dp[u] , pv = dp[v];
int su = sz[u] , sv = sz[v];
dp[u] -= dp[v] + sz[v];
sz[u] -= sz[v];
dp[v] += dp[u] + sz[u];
sz[v] += sz[u];
dfs2(v , u);
dp[u] = pu , dp[v] = pv;
sz[u] = su , sz[v] = sv;
}
}
vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
ans.resize(n , 0);
sz.resize(n, 0);
dp.resize(n , 0);
graph.resize(n , {});
for(auto& edge:edges){
int u = edge[0];
int v = edge[1];
graph[u].emplace_back(v);
graph[v].emplace_back(u);
}
dfs(0 , -1);
dfs2(0 , -1);
return ans;
}
};