均分纸牌

题目链接 AcWing1536. 均分纸牌
问题描述

分析

这道题有个特殊的地方就是A1只能从A2获取纸牌，或者A1只能将多余的纸牌给A2，此操作后A1的纸牌数应该为avg。
A2的纸牌只能从A3获取，或者给A3不能从A1获取，或者给A1，因为A1==avg，这样做会使得操作重复(A1就是通过A2来达到avg的)，这样我们就能知道当前的数Ai要通过Ai+1来达到avg。这里我们从左端A1来考虑，从右端An来考虑也是可以的。

代码如下

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110;
int f[N];
int res=0;

int main(){
    int n,sm=0;
    cin>>n;
    for(int i=1;i<=n;i++){
       scanf("%d",&f[i]);
       sm+=f[i];
    } 
    int avg=sm/n;
    for(int i=1;i<=n;i++)
        if(f[i]!=avg){
            res++;
            f[i+1]+=f[i]-avg;
        }
    cout<<res;
    return 0;
}

糖果传递

问题链接 AcWing122. 糖果传递
问题描述

分析
这道题看起来和上面的题很像，其实题意确实差不多，区别就是上一道题的两端和这道题的两端不同，这道题是一道环型均分纸牌问题，虽然改动了一点，但是解法却完全不同。

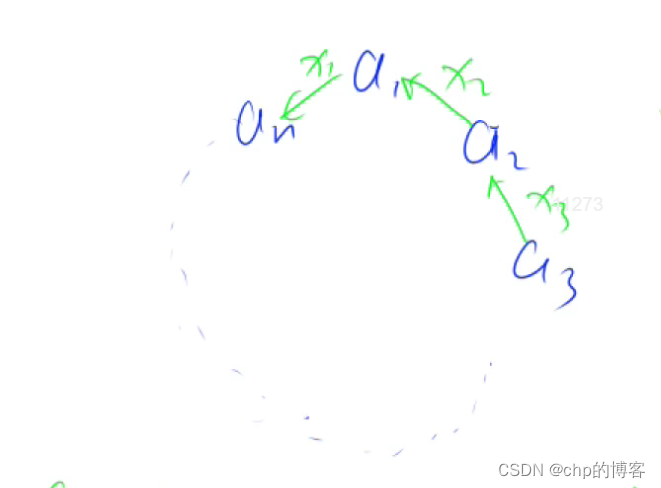
如图所示，a1可以从a2获得x2，a2可以从a3获得x3，… ，an从a1获得x1，其中x2,x3,…,x1可正可负。
我们可以预先得到均分后的糖果数量 avg=(a1+a2+…+an)/n
那么就有

a1+x2-x1=avg
a2+x3-x2=avg
a3+x4-x3=avg
.....
an-1 + xn -xn-1=avg
an +x1-xn=avg

变形后可得

x1-x2=a1-avg
x2-x3=a2-avg
....
xn-1 - xn=an-1 - avg
xn-x1 = an-avg

依次从下往上做累加可得

0=0
x2-x1=(an+an-1+..+a2)-(n-1)*avg
....
xn-1 -x1=(an-1 +an)-2*avg
xn-x1=an-avg

再将x1挪到右边，让x2~xn由x1来表示

x1=x1
x2=x1+(an+an-1+..+a2)-(n-1)*avg
....
xn-1=x1+(an-1 +an)-2*avg
xn=x1+an-avg

再变形,将等式右边转化成差的形式

x1=x1-0
x2=x1-{(n-1)*avg-(an+an-1+..+a2)}
....
xn-1=x1-{2*avg-(an-1 +an)}
xn=x1-{avg-an}

我们的目标是求最小的代价，也就是求最小的|x1|+|x2|+…+|xn|
那么根据上式，

min{|x1|+|x2|+....+|xn|}=min{|x1-0|+|x1-{(n-1)*avg-(an+an-1+..+a2)}|+.....+|x1-{2*avg-(an-1 +an)}|+|x1-{avg-an}|}

其中

min{|x1-0|+|x1-{(n-1)*avg-(an+an-1+..+a2)}|+.....+|x1-{2*avg-(an-1 +an)}|+|x1-{avg-an}|}

是不是看起来很熟悉？这个就是找到一个点x1，让x1到点0,(n-1)avg-(an+an-1+…+a2),…{2avg-(an-1 +an)},{avg-an}的距离和最小，那么这就相当于是一个区间选址问题，那这就很容易解决了。

总结，这道题偏数学，如果第一次遇到很难想出来这种解法

代码如下

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e6+10;

ll f[N];
int h[N];
int main(){
    ll n,avg=0,res=0;
    cin>>n;
    for(int i=0;i<n;i++){
        scanf("%d",&h[i]);
        avg+=h[i];
    }
    avg/=n;
    ll t=0;
    for(int i=0;i<n;i++){
        t+=avg-h[n-i-1];
        f[i]=t;
    }
    sort(f,f+n);
    for(int i=0;i<n;i++)
        res+=abs(f[n>>1]-f[i]);
    cout<<res;
    return 0;
}