光场2.0

1. 发展历程

由于光场1.0从结构上子图像的分辨率严重依赖MLA子透镜的数量，因此分辨率一直受限，限制了光场1.0结构的广泛应用。针对此不足，在2008年，又一篇伟大的论文出现了，该论文提出了全分辨率光场渲染的概念，将光场1.0的图像渲染分辨率可以提高5*10倍左右。该论文的详细链接：全分辨率光场渲染，该文章仅仅是从现象提出了一种全分辨率光场渲染的方法，提出后的几年时间内，多篇针对该相机的进一步探索的论文又对该技术做了进一步探究，包括：The focused plenoptic camera，Focused plenoptic camera and rendering，Depth of Field in Plenoptic Cameras。

2. 结构介绍及原理说明

聚焦型光场相机根据MLA二次成像的虚实分为两种：伽利略型光场相机和开普勒型光场相机。

3. 参数设计

聚焦光场相机的单个透镜成像原理如下图所示：其中d为子透镜的直径，a为二次成像物距，b为二次成像的像距，三者满足单透镜成像共轭关系。

聚焦型光场相机的空间分辨率为探测器图像的分辨率乘以b/a。

每一个微图像对d/b的角度信息进行采样，并对d*a/b的位置信息进行采样，而每一个像素对d/a的角度信息进行采样。因此，聚焦型光场相机的角度分辨率为a/b。

在提取对应的子图像拼接时，子图像的图像块大小：

M = d*b/a

a. F 数匹配

 B 为微透镜阵列面到探测器面的距离，D 为微透镜的孔径，BL 为主透镜出瞳面到探测器面的距离，DL 为主透镜出瞳大小。

b. 虚深度

虚深度是指场景中一物点经过主透镜成像得到的中间像点在被微透镜二次成像时，微透镜的成像物像距之比，即a/B，用Ｍ表示。作为聚焦型光场相机的重要参数，虚深度的大小代表了角度分辨率的大小，图中有个固定的几何关系（注意：此处D‘是一个变量，表示单个物点被MLA平面成像的宽度）：

在满足Ｆ数匹配的条件下，虚深度的值就等于一个物点可以被多少个不同的微透镜成像，每一个微透镜成的像都代表了一个独立的方向信息，因此虚深度的大小表示了光场图像中角度分辨率的大小。为了能够实现三维成像，场景中每一物点应至少被两个微透镜成像，这样才可以通过立体匹配的原理计算出深度，即满足：

M>2

又根据微透镜物像成像关系：

结合两者可得：

a<0伽利略型： ；a>0开普勒型：。当B = f 时，系统结构转变为非聚焦型光场相机。

c. 景深

景深一般是物空间的参数，不过由于聚焦型光场相机是一个二次成像系统，因此对最终成像影响最大的是微透镜成像的景深，也对应着主透镜成像的像深。（景深在像空间的对应量）。

微透镜成像几何关系图：（ａ）削景深示意图，（ｂ）后景深示意图

在考虑景深大小时，我们是将弥散斑大小作为决定量的，设s为探测器的像素大小，其中前后景深分别为：

微透镜景深范围为：

景深大小可近似为：

d. 深度分辨率

在允许的深度范围内，我们可以通过立体匹配的原理实现光场图像的深度估计。那么深度分辨率同样可以由立体匹配原理计算得到。

 （图片说明：d表示MLA的直径，B表示MLA距离CCD的距离，x表示像素距离该像素对应的MLA中心高度的距离，a表示该光线和光轴的交点距离MLA平面的距离。）

可知：

a/B = d/x

a(x) = (1/x)*B*d

将中间像面的深度关系转换到主透镜物空间，即可得到场景的深度信息，设被摄物体到主透镜距离为aL，主透镜焦距为fL，则有：

 aL(x) = [1/fL - 1/(l0+a(x))]^(-1)

……

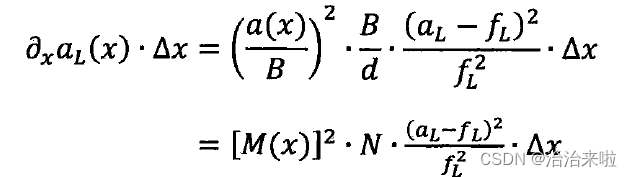
 深度分辨率主要由微透镜成像关系（也即空间分辨率），微透镜工作Ｆ数，主透镜焦距，物距，以及探测器像素尺寸确定。其中，空间分辨率与深度分辨率相互约束，而空间分辨率和工作Ｆ数同时影响了微透镜的景深大小，也造成了对深度分辨率的约束。此外，由于衍射效应，工作Ｆ数又受到了像素尺寸的制约。

实际系统参数计算

实际系统参数计算详见下一篇博文内容。