文章目录

1、 [根据二叉树创建字符串](https://leetcode.cn/problems/construct-string-from-binary-tree/)
2、 [二叉树的层序遍历](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
3、 [二叉树的层序遍历 II](https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/)
4、 [二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
5、 [二叉搜索树与双向链表](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
6、 [从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
7、 [从中序与后序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)
8、 [二叉树的前序遍历-非递归](https://leetcode.cn/problems/binary-tree-preorder-traversal/)
9、 [二叉树的中序遍历-非递归](https://leetcode.cn/problems/binary-tree-inorder-traversal/)
10、 [二叉树的后序遍历-非递归](https://leetcode.cn/problems/binary-tree-postorder-traversal/)

1、根据二叉树创建字符串

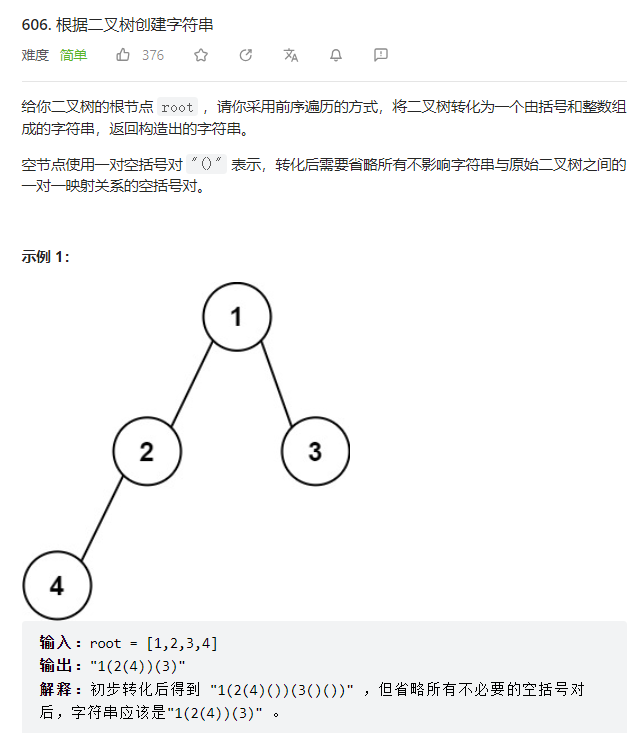
思路图解：

//对于根节点，直接省略
//递归左边：
//1、左为空，右不为空不省略
//2、左不为空,不省略

//递归右边
//3、右不为空不能省略
    string tree2str(TreeNode* root) 
    {
        if(root == nullptr)
            return "";
        string str = to_string(root->val);
        if(root->left || root->right)
        {
            str += '(';
            str += tree2str(root->left);
            str += ')'; 
        }
        if(root->right)
        {
            str += '(';
            str += tree2str(root->right);
            str += ')';
        }
        return str;
    }

2、二叉树的层序遍历

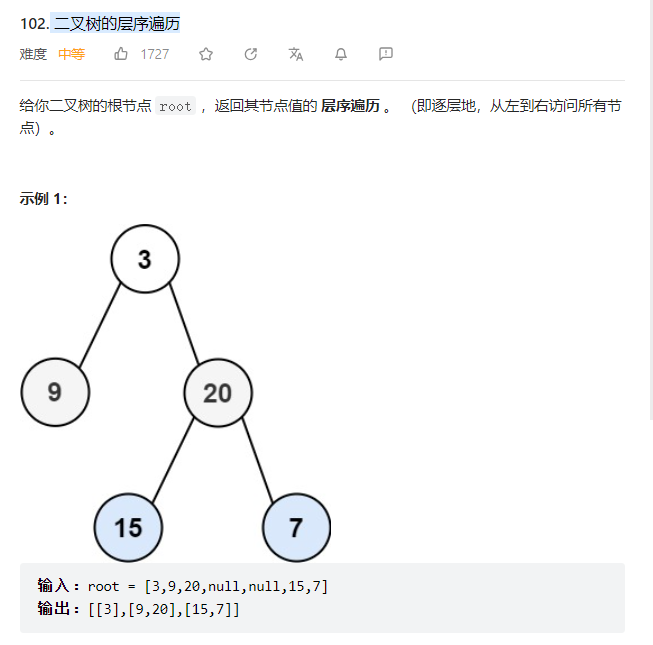
vector<vector<int>> levelOrder(TreeNode* root)
    {
        vector<vector<int>> vv;
        if(root == nullptr)
            return vv;
        queue<TreeNode*> Qdata; //存储数据的队列

        Qdata.push(root);
        int levelSize = 1;
        while(!Qdata.empty())
        { 
            vector<int> v;
            while(levelSize--)
            {
                 TreeNode* front = Qdata.front();
                 Qdata.pop();
                 v.push_back(front->val);

                 if(front->left)
                    Qdata.push(front->left);
                 if(front->right)
                    Qdata.push(front->right);
            }
            vv.push_back(v);
            levelSize = Qdata.size();
        }
        return vv;
    }

3、二叉树的层序遍历 II

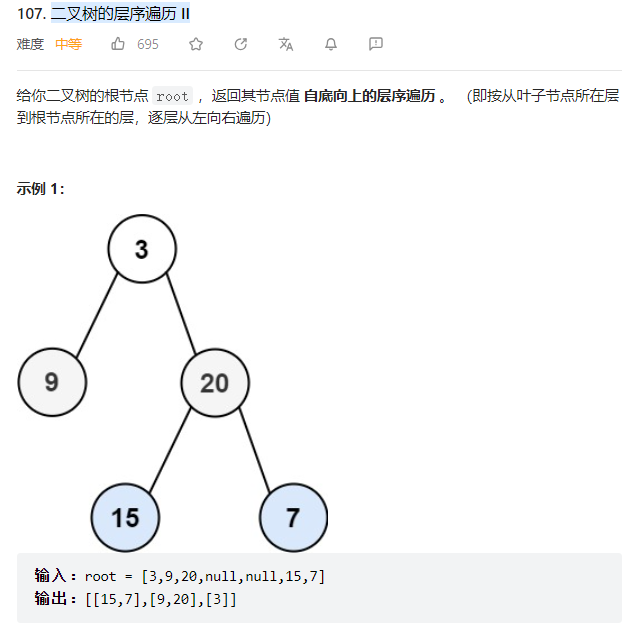
思路：直接将从头层序遍历的结果倒过来即可

vector<vector<int>> levelOrderBottom(TreeNode* root) 
    {
        vector<vector<int>> vv;
        queue<TreeNode*> q1; //节点
        int levelSize = 0;

        if(root != nullptr)
        {
            q1.push(root);
            levelSize = 1;
            
        }
        while(!q1.empty())
        {
            vector<int> v;
            while(levelSize--)
            {
                TreeNode* front = q1.front();
                q1.pop();

                
                v.push_back(front->val);

                if(front->left)
                    q1.push(front->left);
                if(front->right)
                    q1.push(front->right);
            }
            levelSize = q1.size();
            vv.push_back(v);
        }
        reverse(vv.begin(),vv.end());//将结果翻转
        return vv;
    }

4、二叉树的最近公共祖先

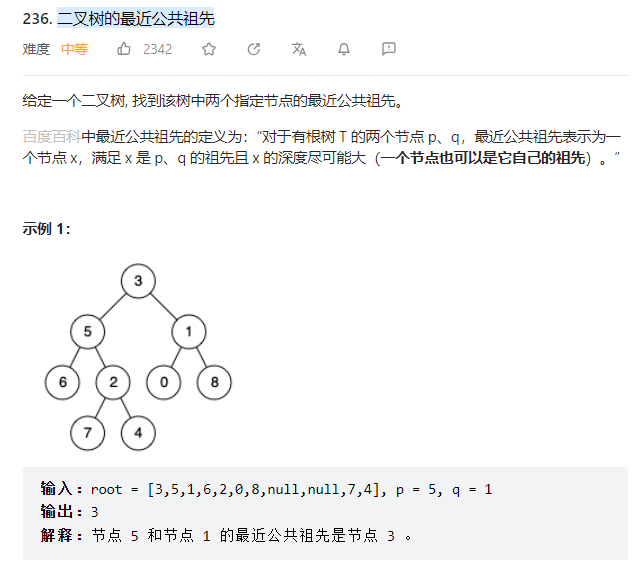
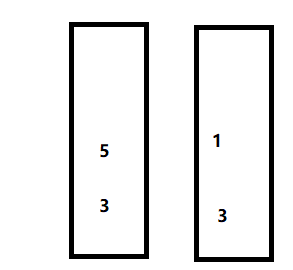
    bool GetPath(TreeNode* root, TreeNode* x,stack<TreeNode*>& path)
    {
        if(root == nullptr)
            return false; 
        //先入栈在判断
        path.push(root);
        //当前节点就是，直接返回
        //当前节点不是再去左边和右边找
        if(root == x)
            return true;
        
        bool Inleft = GetPath(root->left, x,path);
        if(Inleft)    
            return true; //在左边说明这个节点是路径节点，入栈成功

        bool Inright = GetPath(root->right, x,path);
        if(Inright)    
            return true; //在左边说明这个节点是路径节点，入栈成功
        
        //到这里说明不是路径节点
        path.pop();
        return false;
    }


    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        stack<TreeNode*> ppath;
        stack<TreeNode*> qpath;
        
        GetPath(root,p,ppath);
        GetPath(root,q,qpath);

        while(ppath.size() != qpath.size())
        {
            if(ppath.size() > qpath.size())
                ppath.pop();
            else
            {
                qpath.pop();
            }
        }

        while(ppath.top() != qpath.top())
        {
            ppath.pop();
            qpath.pop();
        }
        return ppath.top();
    }

5、二叉搜索树与双向链表

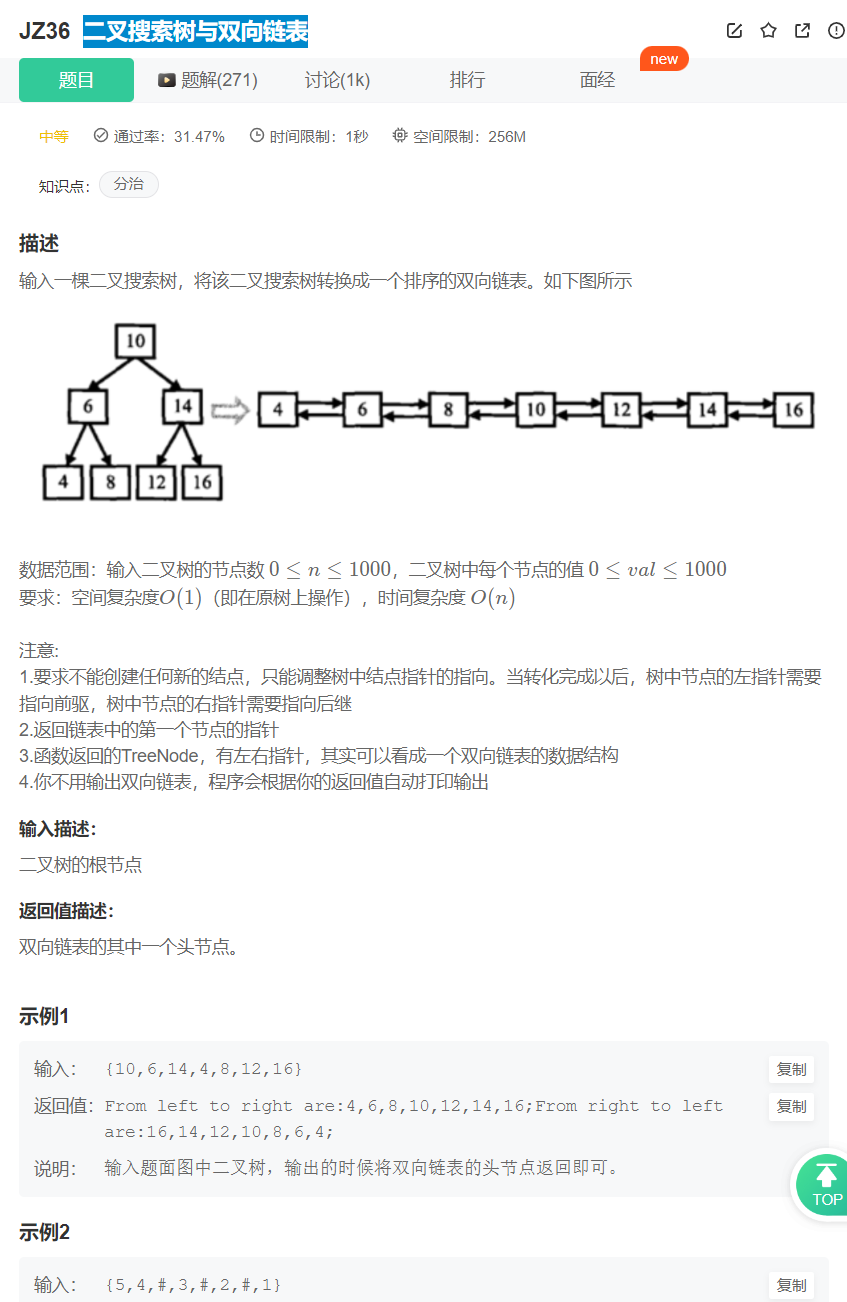
	void InOrder(TreeNode* cur,TreeNode*& prev)
	{
		if(cur == nullptr)
			return;
		InOrder(cur->left,prev);
		//开始操作
		cur->left = prev;
		if(prev)
			prev->right = cur;
		prev = cur;

		InOrder(cur->right,prev);
	}


    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
        if(pRootOfTree == nullptr)
			return nullptr;
		TreeNode* prev = nullptr;
		InOrder(pRootOfTree,prev);

		//找头
		TreeNode* head = pRootOfTree;
		while(head && head->left)
		{
			head = head->left;
		}
		return head;
	}

6、从前序与中序遍历序列构造二叉树

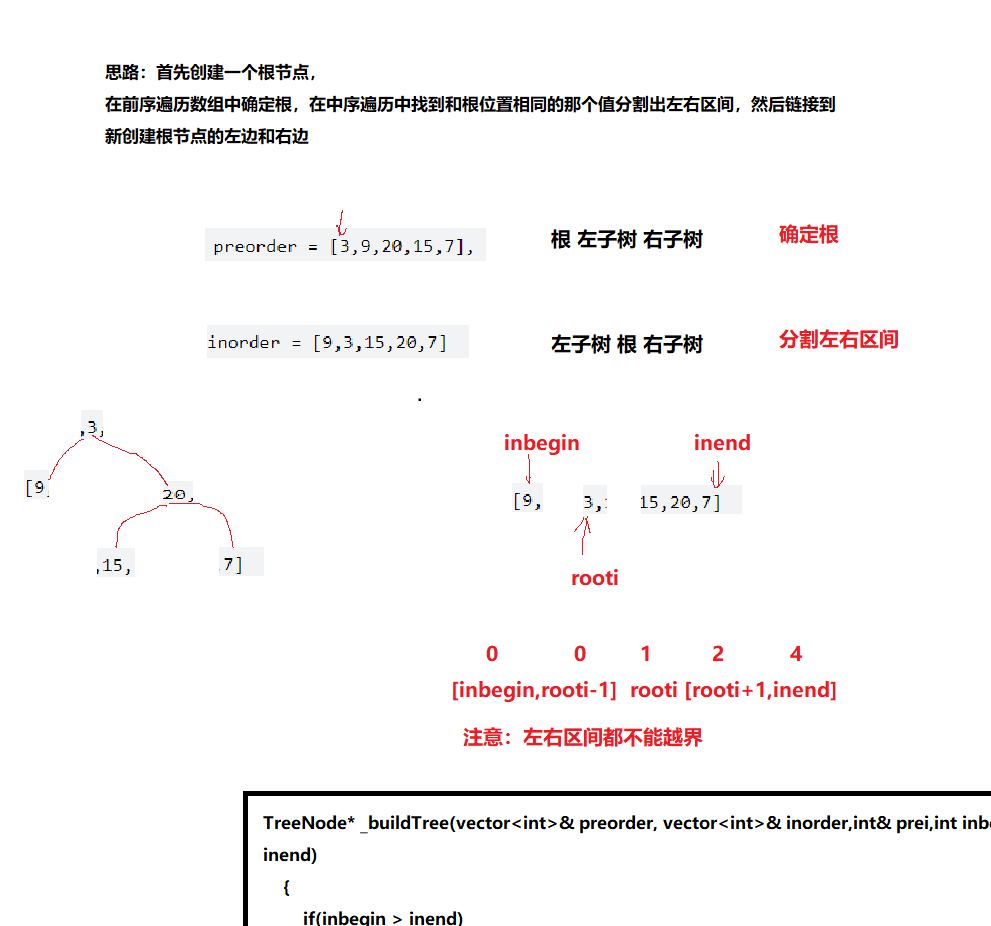
//思路：前序遍历确定跟，根据根的值在中序遍历中分割左右区间，链接在根的左右两侧，
 //然后递归下去

    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& prei,int inbegin,int inend)
    {
        if(inbegin > inend)
            return nullptr;
        TreeNode* root = new TreeNode(preorder[prei]);
        //在中序中找根的位置
        int rooti = inbegin;
        while(inbegin <= inend)
        {
            if(preorder[prei] == inorder[rooti])
                break;
            else
                ++rooti;
        }
        ++prei; //下一个根
        //链接
        root->left = _buildTree(preorder, inorder,prei,inbegin,rooti-1);
        root->right = _buildTree(preorder, inorder,prei,rooti+1,inend);

        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int i = 0;
        return _buildTree(preorder,inorder,i,0,inorder.size()-1);
    }

7、从中序与后序遍历序列构造二叉树

TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin,int inend) 
    {
        if(inbegin > inend)
            return nullptr;
        //先创建一个根
        TreeNode* root = new TreeNode(postorder[posti]);

        //找到根，将中序序列分割为左右子区间
        int rooti = inbegin;
        while(rooti <= inend)
        {
            if(inorder[rooti] == postorder[posti])
                break;
            else
                rooti++;
        }

        posti--;
        //链接[inbegin,rooti-1] rooti [rooti+1,inend]
        //先链接右子树，因为后序遍历是 左子树 右子树 根
        //从后向前就是根 右子树 左子树
        root->right = _buildTree(inorder, postorder,posti,rooti+1,inend);
        root->left = _buildTree(inorder, postorder,posti,inbegin,rooti - 1);
        
        return root;
    }


    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        int i = postorder.size() - 1;
        return _buildTree(inorder, postorder,i,0,inorder.size() - 1); 
    }

8、二叉树的前序遍历-非递归

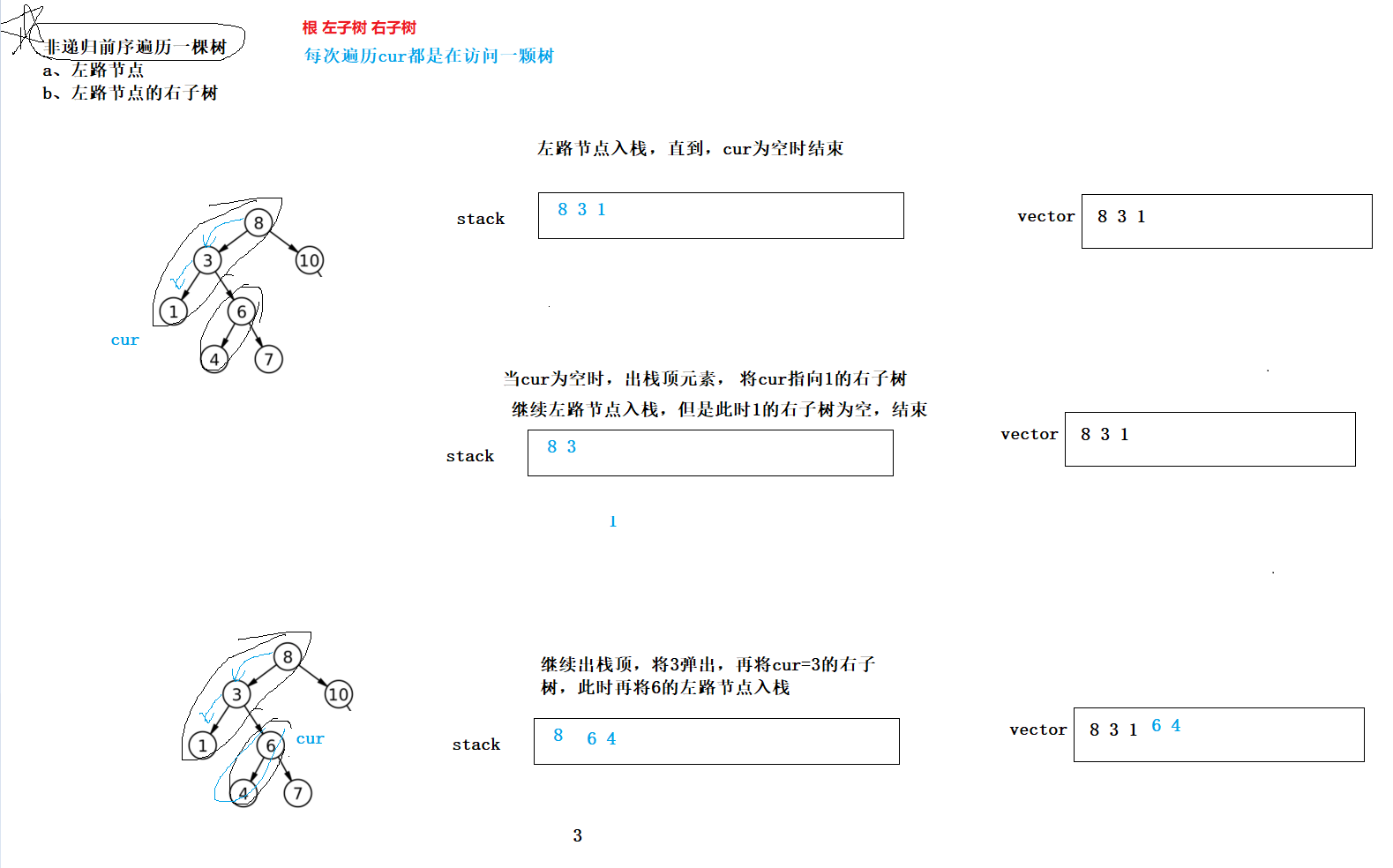
//将一棵树看成是左路节点和左路节点的右子树
//首先定义一个数组用来保存结果，定义一个栈，用来保存左路节点
//因为是前序遍历，首先将左路节点入数组和栈，直到cur是空结束了，
//然后取得栈顶元素，将栈顶的右子树给他（其实就是右路节点），循环出栈即可
    vector<int> preorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            //开始访问一棵树
            //左路节点
            //左路节点的右子树
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }

            //开始访问右子树
            TreeNode* top = st.top();
            st.pop();

            cur = top->right; //子问题访问右子树

        }
        return v;
    }

9、二叉树的中序遍历-非递归

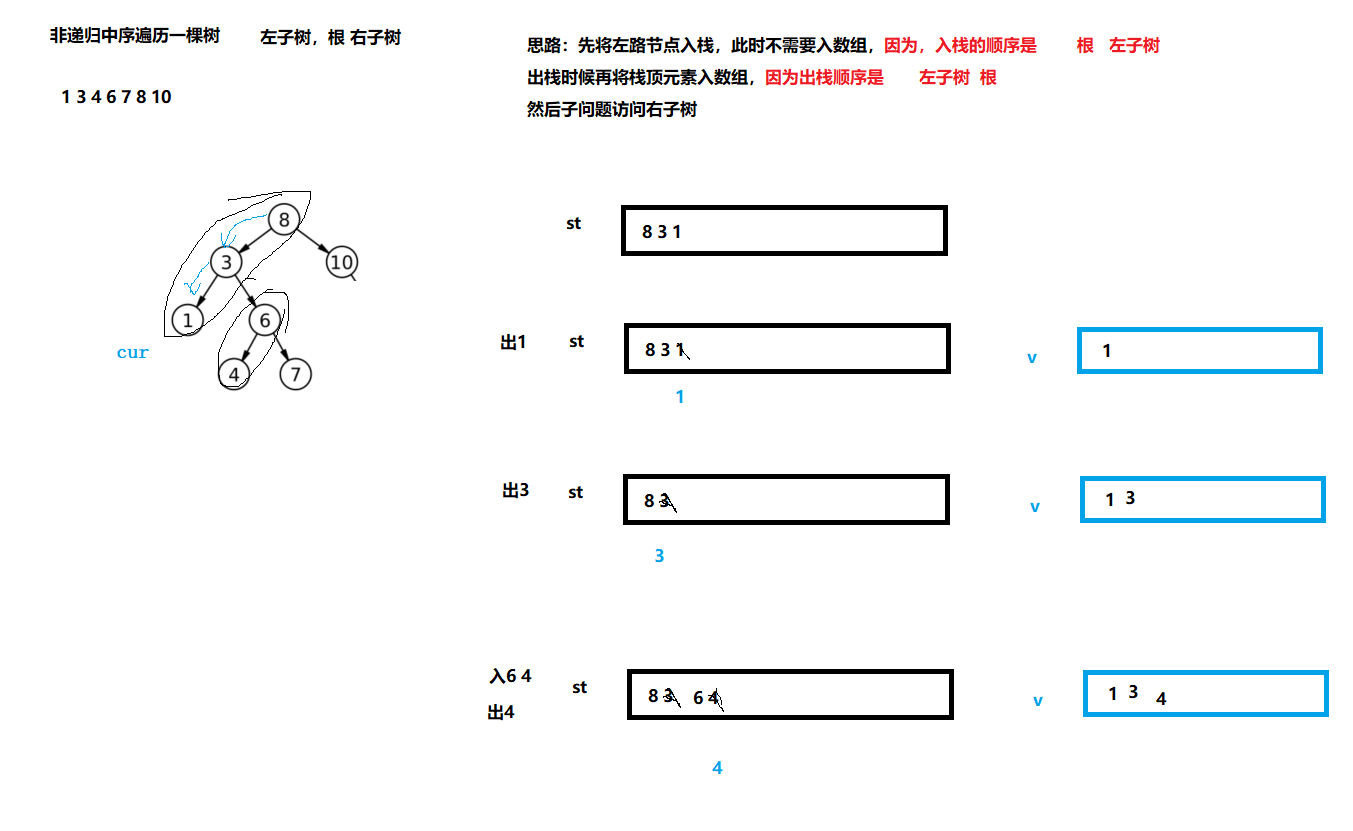
 vector<int> inorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val);

            cur = top->right;//子问题访问右子树
        }
        return v;
    }

10、二叉树的后序遍历-非递归

vector<int> postorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while(cur || !st.empty())
        {
            //左路节点入栈
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();
                prev = top;
            }
            else
            {
                //子问题访问左路节点
                cur = top->right;
            }
        }
        return v;
    }