图源:文心一言
本篇博文含{先序线索化的代码与后序线索化的代码},由于模板字数限制,中序线索化的代码及线索化的原理简介在上一篇博文~🥝🥝
数据结构05:树与二叉树[C++][线索二叉树:中序]_梅头脑_的博客-CSDN博客
- 第1版:查资料、写BUG、画导图、画配图~🧩🧩
- 第2版:改掉了后序的bug,这回后序可以跑了~🧩🧩
- 第3版:改代码、改说明、改配图~🧩🧩
- 发现线索化代码写在main函数里太奇怪了,所以改到了类里,相关代码与注释进行调整~
- 对于不够简洁与可能产生歧义的内容作了调整 {甚至重新画了配图}~
- 增加中序线索化的逆向遍历{在前一篇博文中哦}~
参考用书:王道考研《2024年 数据结构考研复习指导》
参考用书配套视频:5.3_4_线索二叉树的概念_哔哩哔哩_bilibili
特别感谢: Chat GPT老师、BING AI老师、文心一言老师~
📇目录
📇目录
🦮思维导图
⌨️代码实现
🧵先序线索二叉树
🔯P0~P3:同中序二叉树
🔯P5:头结点线索化
🔯P6:二叉树遍历
🔯P8:完整代码
🔯P9:运行结果
🧵后序线索三叉树
🌰后序线索二叉树无法求后序后继
🔯P0:调用库文件
🔯P1:定义结点与指针
🔯P2:封装创建结点
🔯P3:创建传统二叉树(三叉链表)
🔯P4:链表线索化
🔯P5:线索化头结点
🔯P6:二叉树遍历
🔯P7:调用函数
🔯P8:完整代码
🔯P9:执行结果
🔚结语
🦮思维导图

- 本篇仅涉及到线索二叉树:先序、后序的代码;
- 思维导图为整理王道教材第5章 树与二叉树的所有内容,其余学习笔记在以下博客~
- 🌸数据结构05:树与二叉树[C++][二叉树:先序、中序、后序遍历]
- 🌸数据结构05:树与二叉树[C++][哈夫曼树HuffmanTree]
- 🌸数据结构05:树与二叉树[C++][并查集]
- 🌸数据结构05:树与二叉树[C++][线索二叉树:中序]
⌨️代码实现
🧵先序线索二叉树
🔯P0~P3:同中序二叉树
此处不再重述调用库、结点定义、增加结点、创建树的功能~
🔯P4:二叉链表线索化
此处我们仅线索化不含头结点的部分,引用指针p、pre完成线索化~
- 指针p:从根结点开始,负责指向线性表的前驱结点;
- 指针pre:从nullptr开始,负责指向线性表的后继结点;
- 传统先序遍历的顺序是根、左、右~
- 线索化二叉树,且如果想增加头结点,就需要遍历二叉树找到首尾结点~
- 判断指针p是否为空,如果为空则退出递归,不为空则继续执行~
- p指针左子树遍历完成,访问至空指针时,表示该指针可以线索化,p的左子树指针指向前驱结点pre,ltag根据规则置1,完成结点的前驱线索化;
- 若前驱结点pre是否存在且右子树为空,将pre的右子树指针指向后继节点p,ltag根据规则置1,完成结点的后继线索化;
- 更新前驱结点pre为当前p指针,为下一次线索化做准备;
- p指针遍历树的左孩子,访问非空结点时,表示该指针位无需线索化,递归调用本函数; //步骤同传统二叉树中序遍历
- p指针遍历树的右孩子,通过非空结点时,表示该指针位无需线索化,ltag置0,递归调用本函数。 //步骤同传统二叉树遍历
void PreThread(ThreadTree& p, ThreadTree& pre) {
if (p != NULL) {
if (p->lchild == NULL) { // 若左子树为空,完成前驱线索化
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) { //若右子树为空,则完成后继线索化
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
if (p->ltag == 0) { // 若左子树不为空,向左遍历
PreThread(p->lchild, pre);
}
if (p->rtag == 0) { // 若右子树不为空,向右遍历
PreThread(p->rchild, pre);
}
}
}
🔯P5:头结点线索化
备注:此处若无线索化逆向遍历的需求,则头结点不是必须的,反而有头结点增加了代码整体的难度 {头结点和尾结点F的链表相互循环} ~因此小伙伴可以根据个人需要删减本部分代码~
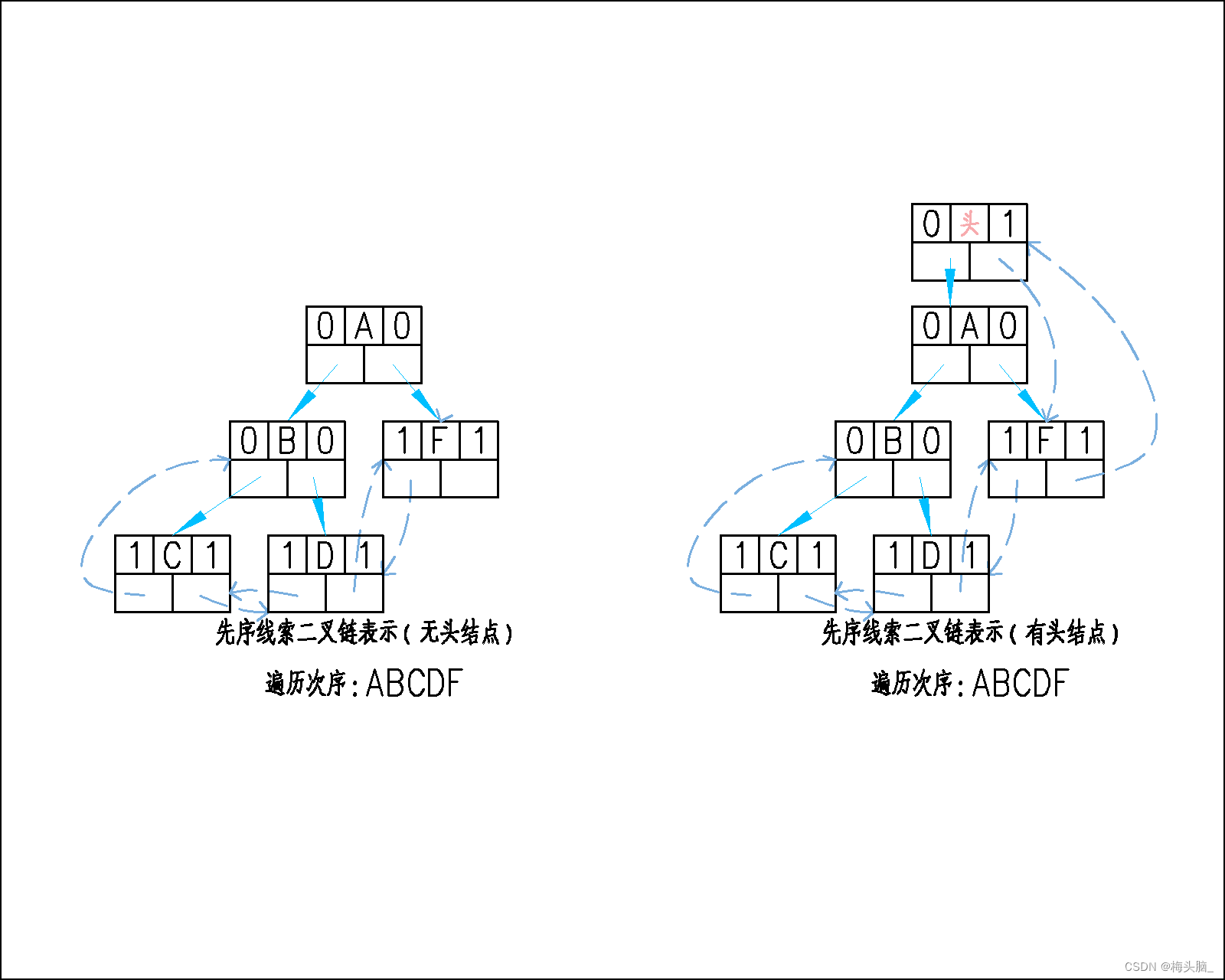
此处我们头结点的处理包含两个内容:
- 创建头结点时的初始化:左指针指向root结点,右线索指向自己;
- 完成线索化,头结点的指针与标志域赋值:尾结点的右线索指向头结点、头结点的右线索指向尾结点~
//头结点初始化
void InitNode() {
head = new ThreadNode();
head->lchild = root;
head->ltag = 0;
head->rchild = head;
head->rtag = 1;
}
//处理头结点线索
void HandleHeadNode(ThreadNode*& head, ThreadNode* lastNode) {
if (lastNode != nullptr && lastNode->rchild == nullptr) { //尾结点右线索指向头结点
lastNode->rchild = head;
lastNode->rtag = 1;
}
//if (head->rchild == nullptr) { // 头结点右线索指向尾结点
head->rchild = lastNode;
head->rtag = 1;
//}
}🔯P6:二叉树遍历
核心思想:找到遍历起始结点,而后有线索则找线索、没线索则找孩子结点~
- 若树非空,继续执行以下语句;
- 将p指向头结点的位置head,其左孩子就是根节点,即为先序遍历的首结点;
- p指针未循环回头结点时,执行以下语句,
- 输出p指针指向当前结点的值;
- 如果p指针指向当前结点的左子树是结点,访问左子树;
- 如果p指针指向当前结点的左子树不是结点,则执行以下语句:
- 如果p指针指向当前结点的右子树是线索,则循环通过右线索找到后继结点;
- 如果p指针指向当前结点的右子树是结点,则通过右孩子指针找到后继结点。
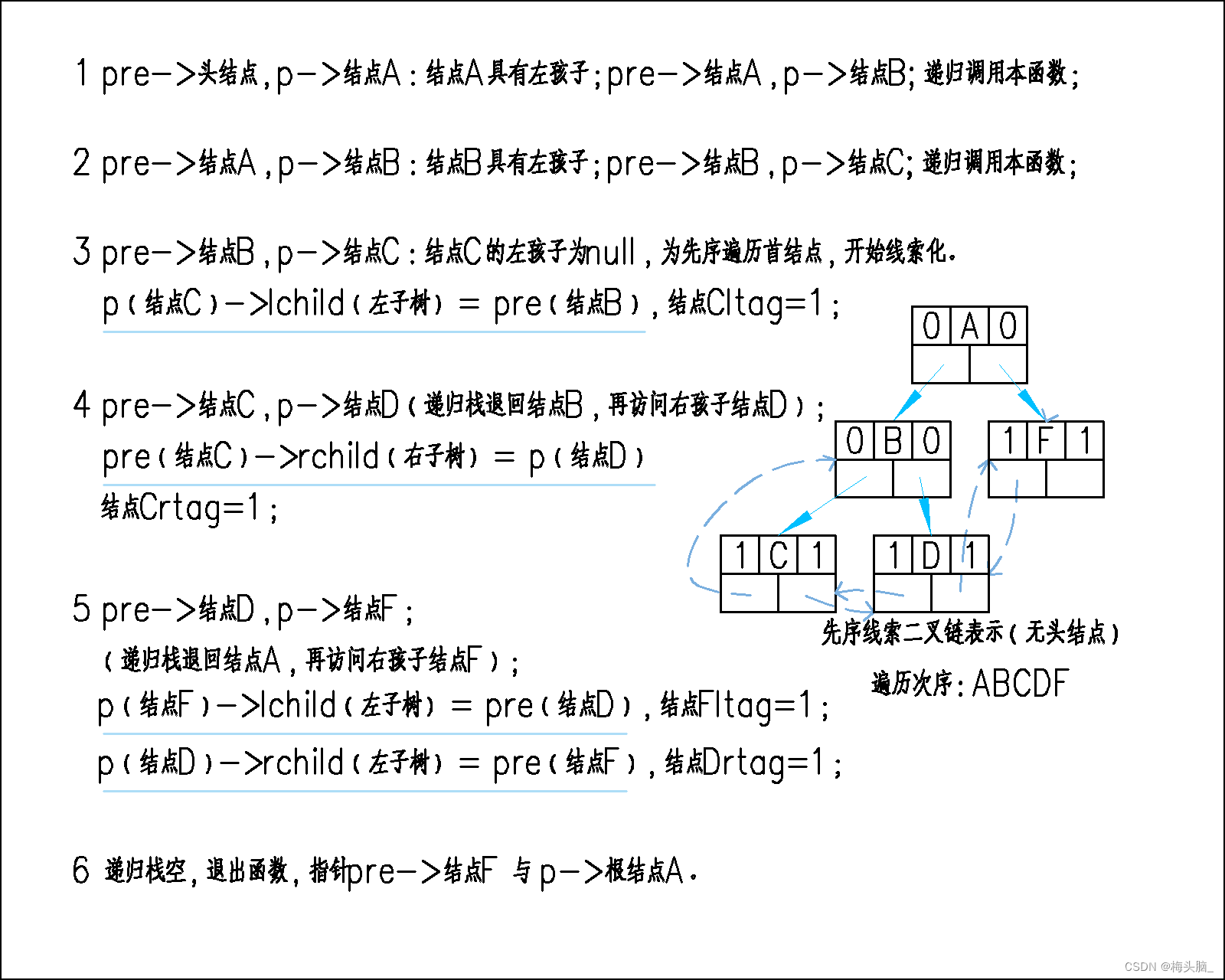
运行起来应该是这样的~
- P指针的路径为头结点,寻找左孩子结点A,打印结点A;
- 结点A具有左孩子结点B,打印结点B;
- 结点B具有左孩子结点C,打印结点C;
- 结点C的右线索指向结点D,打印结点D;
- 结点D的右线索指向结点F,打印结点F;
- 结点F的线索指向头结点,循环判定失败,退出循环。
void PreThreadOrder() {
if (head == NULL) {
std::cout << "树为空!" << std::endl;
return;
}
std::cout << "线索二叉树先序遍历:";
ThreadTree p = head->lchild; // 寻找首结点
while (p != head) { // 若{p不为头结点},继续向后遍历
std::cout << p->data << " "; // 打印结点
if (p->ltag == 0) { // 若{左子树存在结点}
p = p->lchild; // 向左孩子遍历
} else { // 若{左子树不存在结点}
while (p != head && p->rtag == 1) { // 若{右子树存在线索}
p = p->rchild; // 向右线索遍历
std::cout << p->data << " "; // 打印结点
}
p = p->rchild; // {右子树存在孩子},向右孩子遍历
}
if (p->rchild == root || p->rchild == head){ // 尾结点与头结点可能会循环遍历,因此增加判定
break;
}
}
std::cout << std::endl;
}注意: 头结点与尾结点F存在链表循环的现象,因此单独增加了判定{if (p->rchild == root || p->rchild == head)},也就是如果没有头结点的话完全可以删掉这行判定~

🔯P7:调用函数
作用就是个伪main函数,创建了pre指针,并且执行了上述功能~
不喜欢这么写的话,代码保留到处理头结点{handleheadnode}这一行,把遍历放在真main函数里也是可以的~
void ThreadTreeDemo() {
CreateTree();
// 进行线索化
ThreadNode* pre = nullptr;
InThread(root, pre);
// 创建头结点并进行线索化
InitNode();
HandleHeadNode(head, pre);
// 后序遍历
PreThreadOrder();
std::cout << std::endl;
}
🔯P8:完整代码
#include <iostream>
#include <queue>
// 定义结点
typedef struct ThreadNode {
char data;
struct ThreadNode* lchild, * rchild;
int ltag, rtag;
} ThreadNode, * ThreadTree;
// 类:线索化
class ThTree {
// 私有类成员:根结点、头结点
private:
ThreadNode* root;
ThreadNode* head;
// 公共类
public:
// 成员初始化
ThTree() {
root = nullptr;
head = nullptr;
}
// 创建节点
ThreadNode* CreateNode(char data) {
ThreadNode* node = new ThreadNode();
node->data = data;
node->lchild = nullptr;
node->rchild = nullptr;
node->ltag = 0;
node->rtag = 0;
return node;
}
// 构建传统二叉树1
void CreateTree() {
root = CreateNode('A');
root->lchild = CreateNode('B');
root->rchild = CreateNode('F');
root->lchild->lchild = CreateNode('C');
root->lchild->rchild = CreateNode('D');
}
/* 构建传统二叉树2
void CreateTree() {
char rootData;
std::cout << "请输入根节点的数据: ";
std::cin >> rootData;
root = CreateNode(rootData);
std::queue<ThreadNode*> nodeQueue;
nodeQueue.push(root);
while (!nodeQueue.empty()) {
ThreadNode* currentNode = nodeQueue.front();
nodeQueue.pop();
int relation;
std::cout << "请选择节点 " << currentNode->data << " 的孩子结点个数 (1-双孩子结点, 2-左孩子结点, 3-右孩子结点, 4-空孩子结点): ";
std::cin >> relation;
switch (relation) {
case 1: {
char lchildData, rchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* lchildNode = CreateNode(lchildData);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode);
ThreadNode* rchildNode = CreateNode(rchildData);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode);
break;
}
case 2: {
char lchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
ThreadNode* lchildNode = CreateNode(lchildData);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode);
break;
}
case 3: {
char rchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* rchildNode = CreateNode(rchildData);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode);
break;
}
case 4:
// Do nothing for empty child node
break;
default:
std::cout << "无效的选择,请重新输入。\n";
continue;
}
}
}
*/
// 头结点初始化
void InitNode() {
head = new ThreadNode();
head->lchild = root;
head->ltag = 0;
head->rchild = head;
head->rtag = 1;
}
// 头结点线索化
void HandleHeadNode(ThreadNode*& head, ThreadNode* lastNode) {
// if (lastNode != NULL && lastNode->rchild == NULL) {
lastNode->rchild = head;
lastNode->rtag = 1;
// }
// if (head->rchild == NULL) {
head->rchild = lastNode;
head->rtag = 1;
// }
}
// 中序线索化
void PreThread(ThreadTree& p, ThreadTree& pre) {
if (p != NULL) {
if (p->lchild == NULL) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
if (p->ltag == 0) {
PreThread(p->lchild, pre);
}
if (p->rtag == 0) {
PreThread(p->rchild, pre);
}
}
}
// 先序遍历
void PreThreadOrder() {
if (head == NULL) {
std::cout << "树为空!" << std::endl;
return;
}
std::cout << "线索二叉树先序遍历:";
ThreadTree p = head->lchild;
while (p != head) {
std::cout << p->data << " ";
if (p->ltag == 0) {
p = p->lchild;
} else {
while (p != head && p->rtag == 1) {
p = p->rchild;
std::cout << p->data << " ";
}
p = p->rchild;
}
if (p->rchild == root || p->rchild == head){
break;
}
}
std::cout << std::endl;
}
// 执行Demo
void ThreadTreeDemo() {
CreateTree();
ThreadNode* pre = nullptr;
InThread(root, pre);
InitNode();
HandleHeadNode(head, pre);
PreThreadOrder();
std::cout << std::endl;
}
};
int main() {
ThTree* tree = new ThTree();
tree->ThreadTreeDemo();
delete tree;
return 0;
}
🔯P9:运行结果
树1运行结果{代码默认已存小树}:
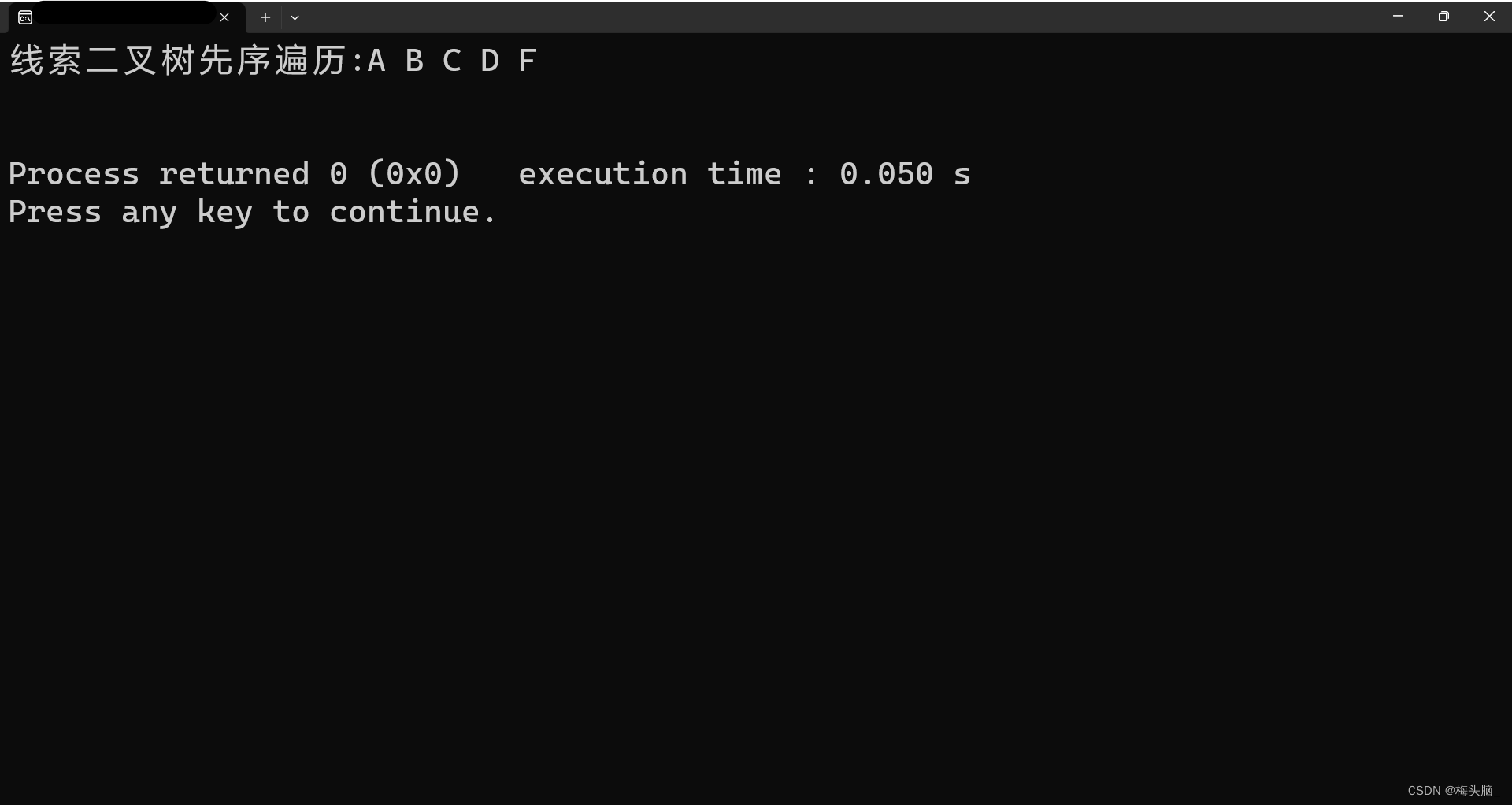
树2运行结果{手动构建小树}:

🧵后序线索三叉树
🌰后序线索二叉树无法求后序后继
根据前述代码及构图,我们知道,先序、中序二叉树可以直接求后序后继:中序二叉树既可以从左向右查询、也可以从右向左查询;先序二叉树可以从上向下查询~
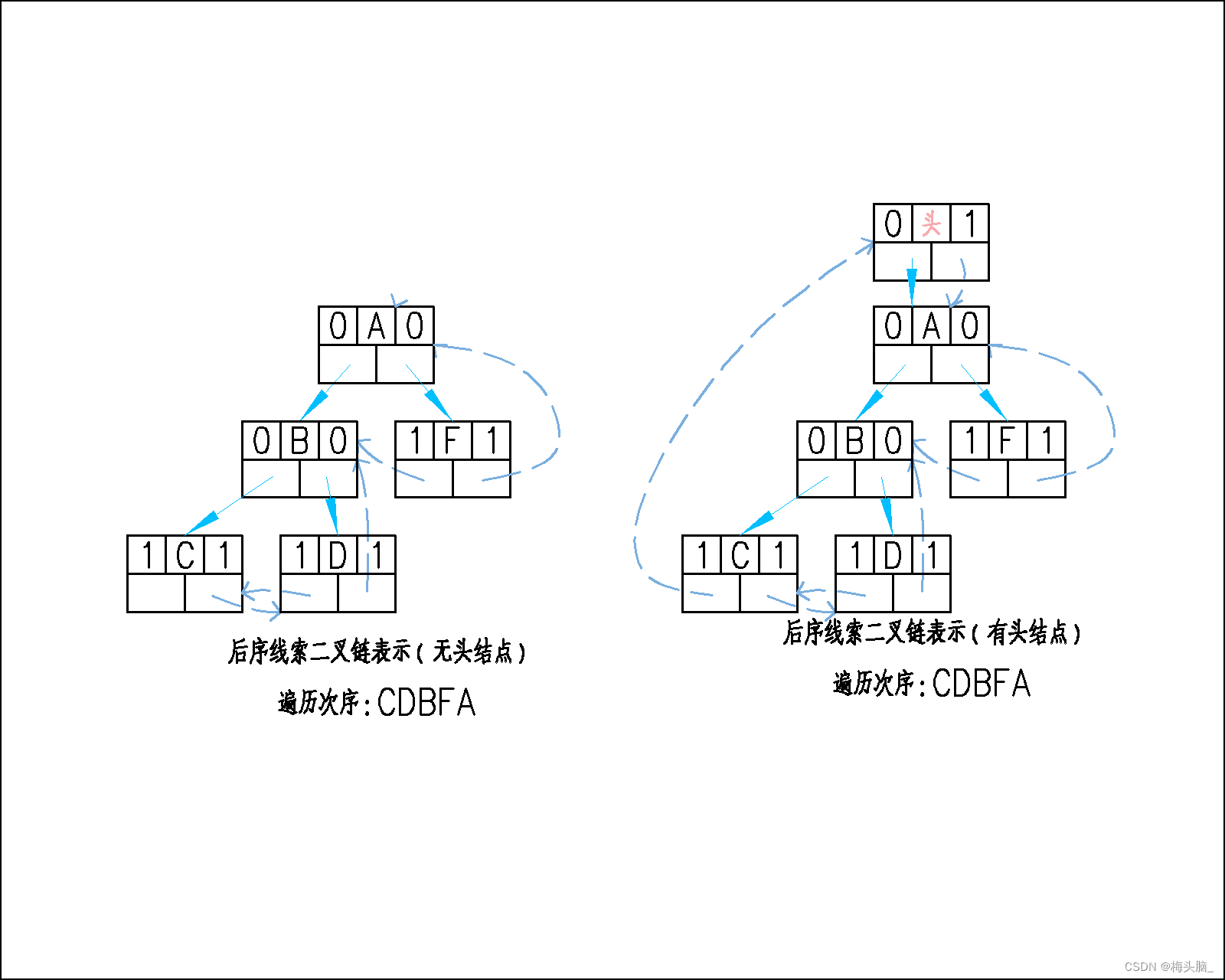
但是后序二叉树这种从下到上就没这么幸运了,我们以图为栗~

- 看向最右下角的后序线索二叉树,后序遍历一路向左,找到结点C为起点;
- 结点C是叶子结点,且是左子树,可以通过线索找到结点D;
- 结点D是叶子结点,且是右子树,可以通过线索找到结点B;
- 结点B非叶子结点,且是左子树,不能通过线索找到结点F;
- 结点F非叶子结点,且是右子树,可以通过线索找到结点A;
- 结点A是根结点,下一个结点是头结点,因此可以结束循环。
出现问题的地方只有B作为非叶子结点,且是左子树时,找不到兄弟结点(如果兄弟结点存在),因此我们引入双亲指针,使结点B通过父节点的孩子结点找到结点F~
话说,万一真考这个也太点背了,不过为了保证博文的完整性还是贴在了这里...
🔯P0:调用库文件
- 输入输出流文件iostream:实现输出文字的效果;
- 辅助队列queue:非必须,仅在有手动创建树的需求时使用,详见下文函数Create Tree;
#include <iostream>
#include <queue>🔯P1:定义结点与指针
此处增加双亲指针*parent~
typedef struct ThreadNode {
char data;
struct ThreadNode* lchild, * rchild, * parent; // 添加parent指针
int ltag, rtag;
} ThreadNode, * ThreadTree;🔯P2:封装创建结点
- CreateNode普通结点:赋值data,并将parent指向父结点~
- CreateRoot根结点:赋值data,但parent指向nullptr,不能作为普通的参数传入,因此写了两个函数~
ThreadNode* CreateNode(char data,ThreadNode*& parent) {
ThreadNode* node = new ThreadNode();
node->data = data;
node->lchild = nullptr;
node->rchild = nullptr;
node->parent = parent;
node->ltag = 0;
node->rtag = 0;
return node;
}
ThreadNode* CreateRoot(char data, std::nullptr_t nullp) {
ThreadNode* newNode = new ThreadNode();
newNode->data = data;
newNode->lchild = nullptr;
newNode->rchild = nullptr;
newNode->parent = nullptr;
newNode->ltag = 0;
newNode->rtag = 0;
return newNode;
}话说,代码有问题询问BING AI老师时,她真的有一点凶;虽然学习的道路有点坎坷,不过最后她还是把我教会了...😢😢

BING AI老师真的怀疑我有没有认真听讲...
🔯P3:创建传统二叉树(三叉链表)
创建树这里给出两个选择,二选一即可~
- 选择一:习惯于C++在线测试代码,或是只想看运行结果的小伙伴,直接粘下面这一段就好了,包含一棵简单小树~🌸在线运行C++(GCC 7.4.0) (json.cn)
void CreateTree() {
root = CreateRoot('A',nullptr);
root->lchild = CreateNode('B', root);
root->rchild = CreateNode('F', root);
root->lchild->lchild = CreateNode('C',root->lchild);
root->lchild->rchild = CreateNode('D',root->lchild);
}- 选择二:需要在命令行自己手动搭建小树的小伙伴,粘下面这一段代码,这段代码使用队列构建树,原理与中序二叉树遍历构建是完全类似的~
- 令用户键入的根结点,创建辅助队列中,根节点入队;
- 辅助队列不为空时,循环执行以下操作:
- 队首结点出队并记录,这个结点就是当前结点;
- 二叉树孩子结点的有顺序,不能颠倒,因此采用switch区分4种情况:
- case-1:具两个孩子结点,令用户键入2个孩子结点,分别初始化,链入当前结点,并加入辅助队列;
- case-2:仅有左孩子节点,令用户键入1个左孩子结点,初始化,链入当前结点,并加入辅助队列;
- case-3:仅有右孩子节点,令用户键入1个右孩子结点,初始化,链入当前结点,并加入辅助队列;
- case-4:没有孩子结点,跳过分支,执行下一个循环
void CreateTree() {
char rootData;
std::cout << "请输入根节点的数据: ";
std::cin >> rootData;
root = CreateRoot(rootData, nullptr);
std::queue<ThreadNode*> nodeQueue;
nodeQueue.push(root);
while (!nodeQueue.empty()) {
ThreadNode* currentNode = nodeQueue.front();
nodeQueue.pop();
int relation;
std::cout << "请选择节点 " << currentNode->data << " 的孩子结点个数 (1-双孩子结点, 2-左孩子结点, 3-右孩子结点, 4-空孩子结点): ";
std::cin >> relation;
switch (relation) {
case 1: {
char lchildData, rchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* lchildNode = CreateNode(lchildData,currentNode);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode); // 将左孩子节点加入队列
ThreadNode* rchildNode = CreateNode(rchildData,currentNode);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode); // 将右孩子节点加入队列
break;
}
case 2: {
char lchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
ThreadNode* lchildNode = CreateNode(lchildData,currentNode);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode); // 将左孩子节点加入队列
break;
}
case 3: {
char rchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* rchildNode = CreateNode(rchildData,currentNode);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode); // 将右孩子节点加入队列
break;
}
case 4:
// Do nothing for empty child node
break;
default:
std::cout << "无效的选择,请重新输入。\n";
continue;
}
}
}🔯P4:链表线索化
此处我们仅线索化不含头结点的部分,引用指针p、pre完成线索化~
- 指针p:从根结点开始,负责指向线性表的前驱结点;
- 指针pre:从nullptr开始,负责指向线性表的后继结点;
- 传统后序遍历的顺序是左子树、右子树、根结点~
- 原理十分雷同于前、中遍历,算法还是在传统遍历的基础上增加线索化过程,此处不再赘述~
void PostThread(ThreadTree& p, ThreadTree& pre) {
if (p != nullptr) {
PostThread(p->lchild, pre);
PostThread(p->rchild, pre);
if (p->lchild == nullptr) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != nullptr && pre->rchild == nullptr) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
}
}线索化完成后大概就是下面的样子~
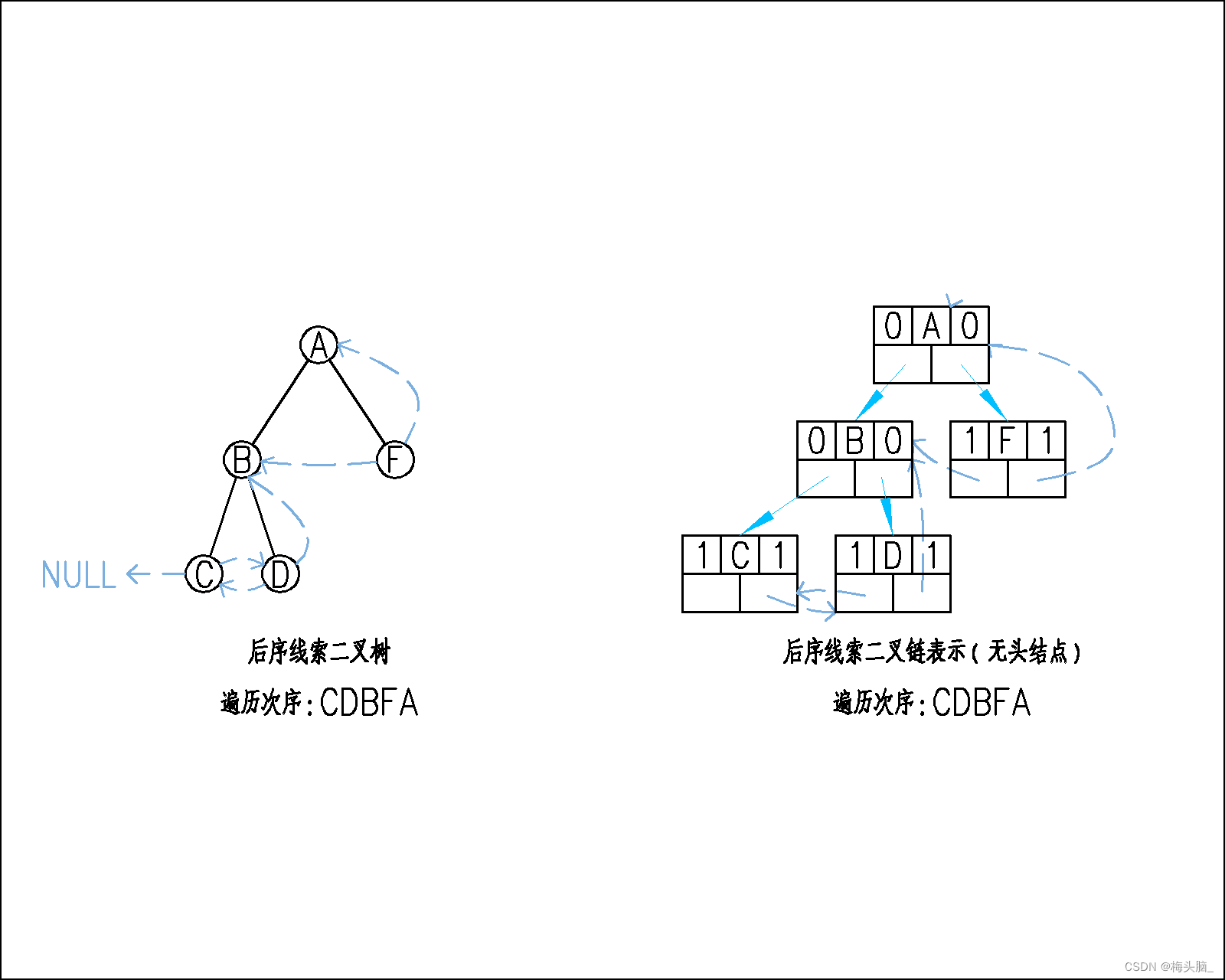
🔯P5:线索化头结点
备注:此处若无线索化逆向遍历的需求,则头结点不是必须的,反而有头结点增加了代码整体的难度 {头结点和尾结点F的链表相互循环} ~因此小伙伴可以根据个人需要删减本部分代码~
此处我们头结点的处理包含两个内容:
- 创建头结点时的初始化:左指针指向root结点,右线索指向自己;
- 完成线索化,头结点的指针与标志域赋值:首结点的左指针指向头结点~
void HandleHeadNode(ThreadNode*& head, ThreadNode* lastNode) {
if (lastNode != NULL && lastNode->rchild == NULL) { // 尾结点右线索指向头结点
lastNode->rchild = head;
lastNode->rtag = 1;
}
// if (head->rchild == NULL) { // 头结点右线索指向尾结点
head->rchild = lastNode;
head->rtag = 1;
// }
}注意: “if (lastNode != NULL && lastNode->rchild == NULL)”这句判定不能丢掉,否则根结点A就会将指向右节点F的指针指向头结点~
🔯P6:二叉树遍历
代码首先从首结点开始,每一轮都会令指针P走向当前结点的父节点,然后遍历父节点的右子树,具体如下~
- 若树非空,继续执行以下语句;
- 设定p指针指向头结点的位置,root指针为根结点,初始置空;
- 遍历p指针的最左侧,即为后序遍历开始的位置;
- 如果p指针不为空时,开始循环;
- 如果p指针的右线索存在,且右线索不指向root:p指针根据右线索寻找后继结点;
- 如果p指针的右线索不在:结合前述判定,这是父结点具有右子树的结点;
- p指针移动到父节点;
- 如果p指针指向的结点具有右子树,p指针移动右孩子结点的位置;
- 如果p指针指向的结点具有左子树,执行循环访问右子树最左侧,即该右子树后序遍历开始的位置~
- 打印p指针指向的结点~
void PostThreadOrder() {
if (head == NULL) {
std::cout << "树为空!" << std::endl;
return;
}
std::cout << "线索二叉树后序遍历:";
ThreadNode* p = head->lchild;
while (p->lchild != nullptr && p->ltag == 0) { // 寻找第一个被线索化的节点(最左边的节点)
p = p->lchild;
}
while (p->rchild != root) {
std::cout << p->data << " "; // 输出节点的值
if (p->rtag == 1 && p->rchild != root) { // 如果节点的右指针是线索,直接转到后继节点
p = p->rchild;
} else { // 否则,节点的右孩子是已经遍历的孩子结点,因此先退回到该节点的父结点
if(p != root){
p = p->parent;
}
if (p->rtag == 0 && p->rchild != root) { // 该结点具有右孩子,则访问右孩子
p = p->rchild;
while (p->ltag == 0 && p->lchild != nullptr) { // 找到右子树最左侧的结点
p = p->lchild;
}
std::cout << p->data << " "; // 输出结点的值
}
}
}
std::cout << p->rchild->data << " "; // 输出根结点的值
}注意:“while (p->rchild != root)”,而不是“while (p != head)”因为在结点A与结点F之间有可能打循环,因此修改了判定~

根据上图,运行起来应该是这样的~
- P指针的路径一路向左,结点A、结点B、结点C,结点C设为起始遍历结点;
- 打印结点C;
- 结点C具有右线索,顺着线索找到结点D,打印结点D;
- 结点D具有右线索,顺着线索找到结点B,打印结点B;
- 结点B没有右线索,需要访问其父节点,如果有父结点有右子树,找到右子树左侧的结点F,打印结点F;
- 结点F具有右线索,顺着线索找到结点A,打印结点A;
- 结点A的线索指向头结点,循环判定失败,退出循环。
🔯P7:调用函数
作用就是个伪main函数,创建了pre指针,并且执行了上述功能~
不喜欢这么写的话,代码保留到处理头结点{handleheadnode}这一行,把遍历放在真main函数里也是可以的~
void ThreadTreeDemo() {
CreateTree();
// 进行线索化
ThreadNode* pre = nullptr;
InThread(root, pre);
// 创建头结点并进行线索化
InitNode();
HandleHeadNode(head, pre);
// 后序遍历
PostThreadOrder();
std::cout << std::endl;
}
🔯P8:完整代码
上次代码的错误是树最后的指针赋值有误,以及判断条件有误,这次手工改掉,应该终于可以跑了,开心~这次把线索化都扔进了类里,应该可以加强一点实用性~
#include <iostream>
#include <queue>
// 定义结点
typedef struct ThreadNode {
char data;
struct ThreadNode* lchild, * rchild, * parent;
int ltag, rtag;
} ThreadNode, * ThreadTree;
// 类:线索化
class ThTree {
// 私有类成员:根结点、头结点
private:
ThreadNode* root;
ThreadNode* head;
// 公共类
public:
// 成员初始化
ThTree() {
root = nullptr;
head = nullptr;
}
// 创建节点
ThreadNode* CreateNode(char data,ThreadNode*& parent) {
ThreadNode* node = new ThreadNode();
node->data = data;
node->lchild = nullptr;
node->rchild = nullptr;
node->parent = parent;
node->ltag = 0;
node->rtag = 0;
return node;
}
ThreadNode* CreateRoot(char data, std::nullptr_t nullp) {
ThreadNode* newNode = new ThreadNode();
newNode->data = data;
newNode->lchild = nullptr;
newNode->rchild = nullptr;
newNode->parent = nullptr;
newNode->ltag = 0;
newNode->rtag = 0;
return newNode;
}
// 构建传统二叉树1
void CreateTree() {
root = CreateRoot('A',nullptr);
root->lchild = CreateNode('B', root);
root->rchild = CreateNode('F', root);
root->lchild->lchild = CreateNode('C',root->lchild);
root->lchild->rchild = CreateNode('D',root->lchild);
}
/* 构建传统二叉树2
void CreateTree() {
char rootData;
std::cout << "请输入根节点的数据: ";
std::cin >> rootData;
root = CreateRoot(rootData, nullptr);
std::queue<ThreadNode*> nodeQueue;
nodeQueue.push(root);
while (!nodeQueue.empty()) {
ThreadNode* currentNode = nodeQueue.front();
nodeQueue.pop();
int relation;
std::cout << "请选择节点 " << currentNode->data << " 的孩子结点个数 (1-双孩子结点, 2-左孩子结点, 3-右孩子结点, 4-空孩子结点): ";
std::cin >> relation;
switch (relation) {
case 1: {
char lchildData, rchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* lchildNode = CreateNode(lchildData,currentNode);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode); // 将左孩子节点加入队列
ThreadNode* rchildNode = CreateNode(rchildData,currentNode);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode); // 将右孩子节点加入队列
break;
}
case 2: {
char lchildData;
std::cout << "请输入左孩子结点的数据: ";
std::cin >> lchildData;
ThreadNode* lchildNode = CreateNode(lchildData,currentNode);
currentNode->lchild = lchildNode;
nodeQueue.push(lchildNode); // 将左孩子节点加入队列
break;
}
case 3: {
char rchildData;
std::cout << "请输入右孩子结点的数据: ";
std::cin >> rchildData;
ThreadNode* rchildNode = CreateNode(rchildData,currentNode);
currentNode->rchild = rchildNode;
nodeQueue.push(rchildNode); // 将右孩子节点加入队列
break;
}
case 4:
// Do nothing for empty child node
break;
default:
std::cout << "无效的选择,请重新输入。\n";
continue;
}
}
}
*/
// 头结点初始化
void InitNode() {
head = new ThreadNode();
head->lchild = root;
head->ltag = 0;
head->rchild = head;
head->rtag = 1;
head->parent = nullptr;
}
// 头结点线索化
void HandleHeadNode(ThreadNode*& head, ThreadNode* lastNode) {
if (lastNode != NULL && lastNode->rchild == NULL) {
lastNode->rchild = head;
lastNode->rtag = 1;
}
// if (head->rchild == NULL) {
head->rchild = lastNode;
head->rtag = 1;
// }
}
// 后序线索化
void PostThread(ThreadTree& p, ThreadTree& pre) {
if (p != nullptr) {
PostThread(p->lchild, pre);
PostThread(p->rchild, pre);
if (p->lchild == nullptr) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != nullptr && pre->rchild == nullptr) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
}
}
// 后序遍历
void PostThreadOrder() {
if (head == NULL) {
std::cout << "树为空!" << std::endl;
return;
}
std::cout << "线索二叉树后序遍历:";
ThreadNode* p = head->lchild;
while (p->lchild != nullptr && p->ltag == 0) {
p = p->lchild;
}
while (p->rchild != root) {
std::cout << p->data << " ";
if (p->rtag == 1 && p->rchild != root) {
p = p->rchild;
} else {
if(p != root){
p = p->parent;
}
if (p->rtag == 0 && p->rchild != root) {
p = p->rchild;
while (p->ltag == 0 && p->lchild != nullptr) {
p = p->lchild;
}
std::cout << p->data << " ";
}
}
}
std::cout << p->rchild->data << " ";
}
// 执行Demo
void ThreadTreeDemo() {
CreateTree();
ThreadNode* pre = nullptr;
InThread(root, pre);
InitNode();
HandleHeadNode(head, pre);
PostThreadOrder();
std::cout << std::endl;
}
};
int main() {
ThTree* tree = new ThTree();
tree->ThreadTreeDemo();
delete tree;
return 0;
}
🔯P9:执行结果
树1{代码已有小树}:
树2{可自定义小树}:
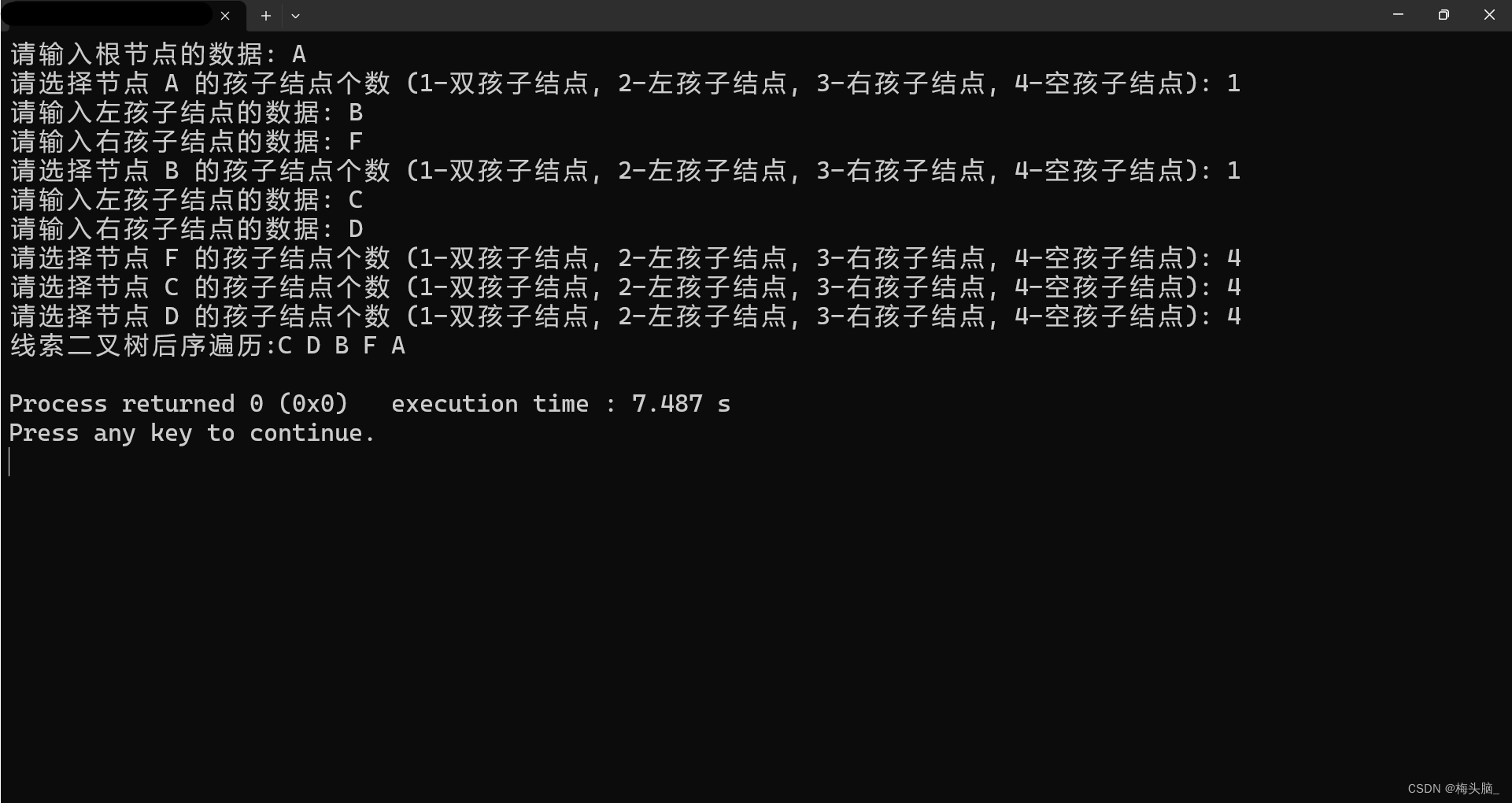
🔚结语
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容{例如有错误、难理解、不简洁、缺功能}等~😶🌫️
博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,收到点赞的话,博主肝文的动力++~🌟🌟