详细描述
Web 服务器对于 HTTP 请求的响应头中缺少 Referrer-Policy,这将导致浏览器提供的安全特性失效。 当用户在浏览器上点击一个链接时,会产生一个 HTTP 请求,用于获取新的页面内容,而在该请求的报头中,会包含一个 Referrer,用以指定该请求是从哪个页面跳转页来的,常被用于分析用户来源等信息。但是也成为了一个不安全的因素,所以就有了 Referrer-Policy,用于过滤 Referrer 报头内容,其可选的项有: no-referrer no-referrer-when-downgrade origin origin-when-cross-origin same-origin strict-origin strict-origin-when-cross-origin unsafe-url 漏洞危害: Web 服务器对于 HTTP 请求的响应头中缺少 Referrer-Policy,这将导致浏览器提供的安全特性失效,更容易遭受 Web 前端黑客攻击的影响。
解决办法
1)修改服务端程序,给 HTTP 响应头加上 Referrer-Policy 如果是 java 服务端,可以使用如下方式添加 HTTP 响应头 response.setHeader(“Referrer-Policy”, “value”) 如果是 php 服务端,可以使用如下方式添加 HTTP 响应头 header(“Referrer-Policy: value”) 如果是 asp 服务端,可以使用如下方式添加 HTTP 响应头 Response.AddHeader “Referrer-Policy”, “value” 如果是 python django 服务端,可以使用如下方式添加 HTTP 响应头 response = HttpResponse() response[“Referrer-Policy”] = “value” 如果是 python flask 服务端,可以使用如下方式添加 HTTP 响应头 response = make_response() response.headers[“Referrer-Policy”] = “value”;
2)修改负载均衡或反向代理服务器,给 HTTP 响应头加上 Referrer-Policy 如果使用 Nginx、Tengine、Openresty 等作为代理服务器,在配置文件中写入如下内容即可添加 HTTP 响应头: add_header Referrer-Policy value; 如果使用 Apache 作为代理服务器,在配置文件中写入如下内容即可添加 HTTP 响应头: Header add Referrer-Policy “value”。
实战
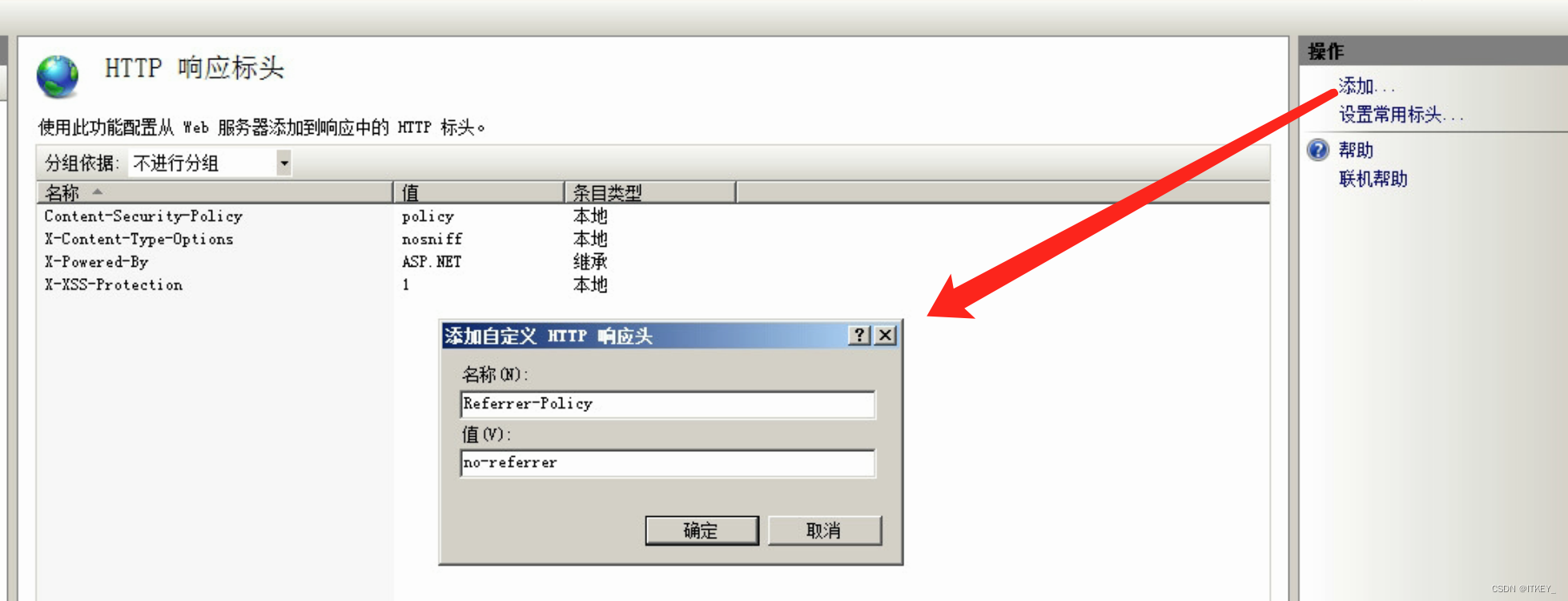
解决办法就是设置header
Referrer-Policy: no-referrerReferrer-Policy: no-referrer
具体的参考:
https://blog.csdn.net/lxyoucan/article/details/131725900