概述

当我们在高等数学中研究函数的极限时，夹逼准则和泰勒公式是两个重要的概念和工具。

夹逼准则（夹挤准则或挤压准则）是用于证明函数极限存在或计算极限值的一种方法。它适用于那些难以直接计算极限的函数，通过将其夹在两个已知函数之间，利用已知函数的极限性质来推导出待求函数的极限。夹逼准则的核心思想是，如果一个函数在某一点附近被两个已知函数夹住，并且这两个已知函数的极限都存在且相等，那么待求函数的极限也存在且等于这个共同的极限值。

泰勒公式是一种用于近似表示函数的方法，它将一个函数在某一点处展开成无穷级数的形式。泰勒公式利用了函数在某一点处的各阶导数的信息，通过展开项的不断增多，可以更准确地逼近原函数的值。泰勒公式可以将复杂的函数用一系列简单的代数式来表示，从而简化计算和分析的过程。通常，泰勒公式包括泰勒级数和带余项的形式，其中带余项描述了近似的误差范围。

在高等数学中，夹逼准则和泰勒公式是常用的工具和技巧，它们在函数极限、函数逼近和级数等领域具有广泛的应用。通过运用夹逼准则，我们可以证明函数的极限存在性和计算极限值；而使用泰勒公式，我们可以近似计算复杂函数的值，并对函数在某一点附近的行为进行研究。这些工具为我们理解和分析数学问题提供了便利，同时也为其他学科中的应用问题提供了数学建模和计算的基础。

（5）利用夹逼准则求极限（后面几个方法一般用来求数列极限）

注意不存在为无穷也可以，主要是两边的极限值相等

例66

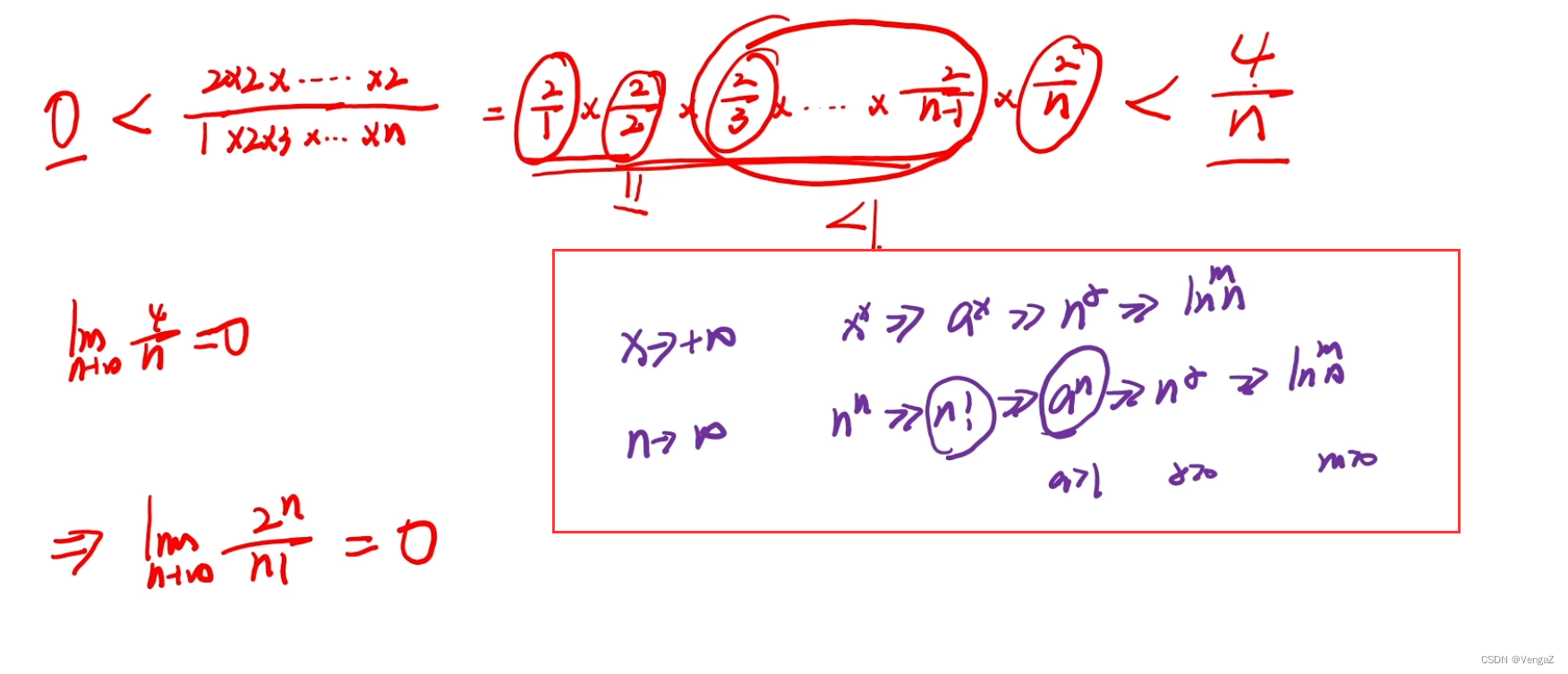
例68（结论，需要记住）

例69（上题的运用，需要数形结合，找出各个区间最大的）

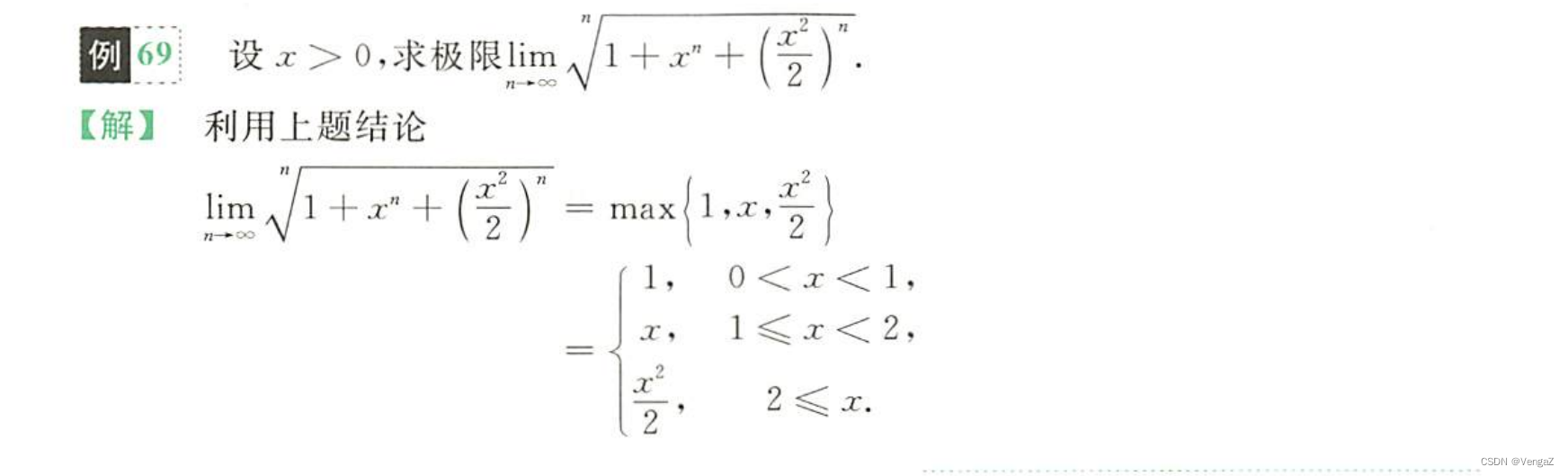
例70

法二
非未定式直接得出答案

例71

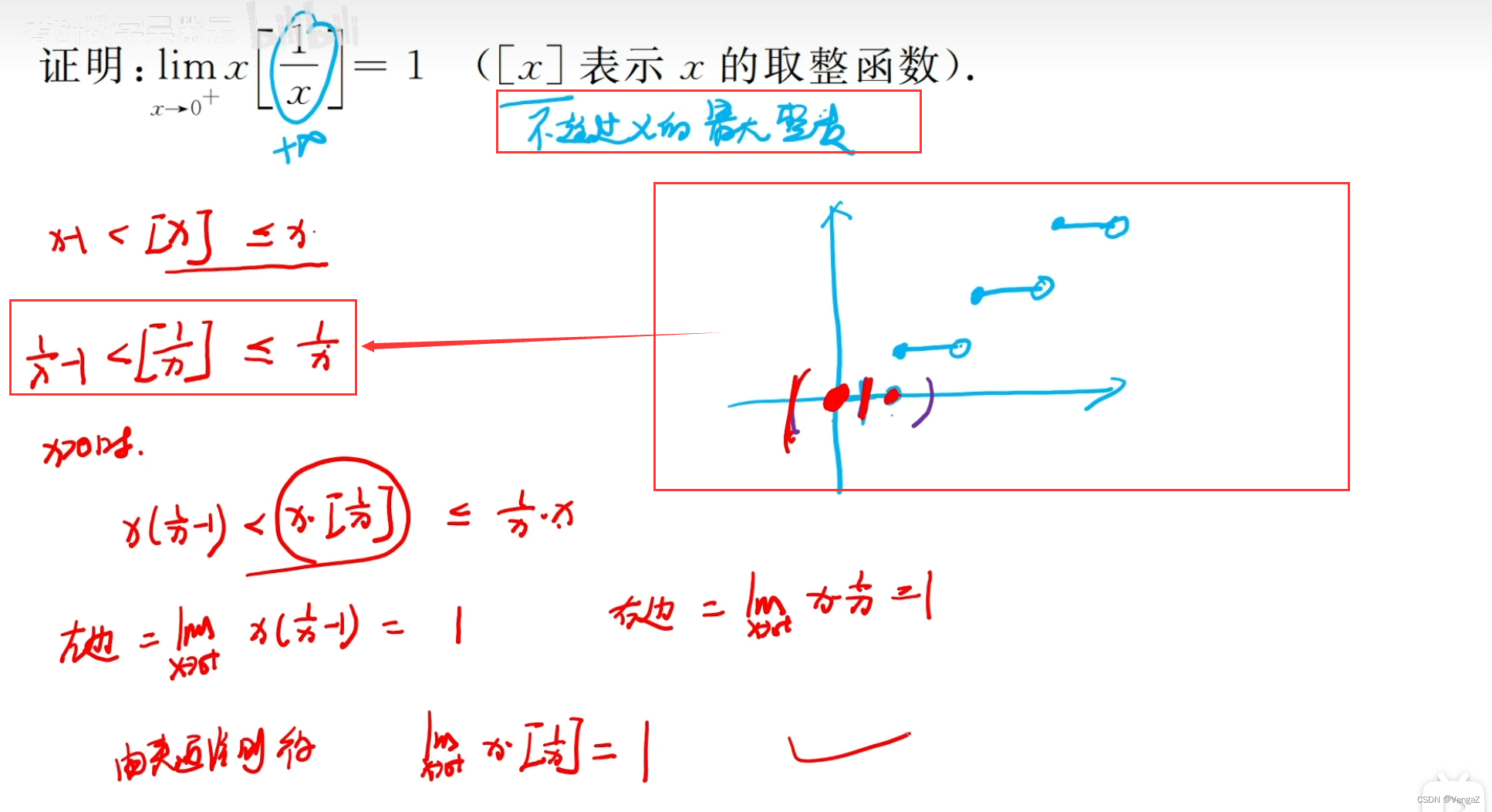
（6）利用单调有界数列极限准则求极限

证明有界性和单调性的方法

这边第三种证明单调性的方式，只有导数大于0能证明，递小于0不能证明单调性
并且需要知道x1和x2的大小关系

例72（***）

先有界后单调

这里知道前几项的大小关系，所以可以直接用函数的导数求单调，下边例题73就不行，因为不知道大小关系

例73 （不等式放缩，不知道前几项的大小关系，故不能用函数求）

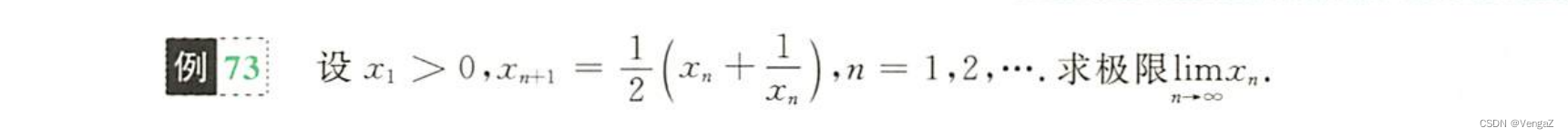
例74 （很妙）

（7）利用无穷小的性质求极限

例75

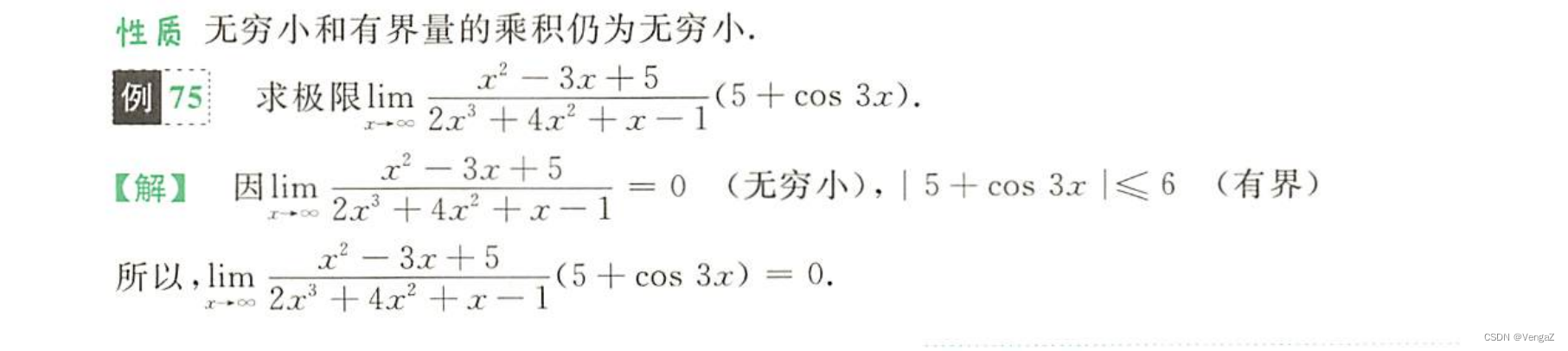
（8）利用函数的连续性求极限

3是一个定式

（9）利用泰勒公式求极限

皮亚诺&拉格朗日

皮亚诺一般用来求极限，拉格朗日的泰勒公式一般用来证明

常见的泰勒公式

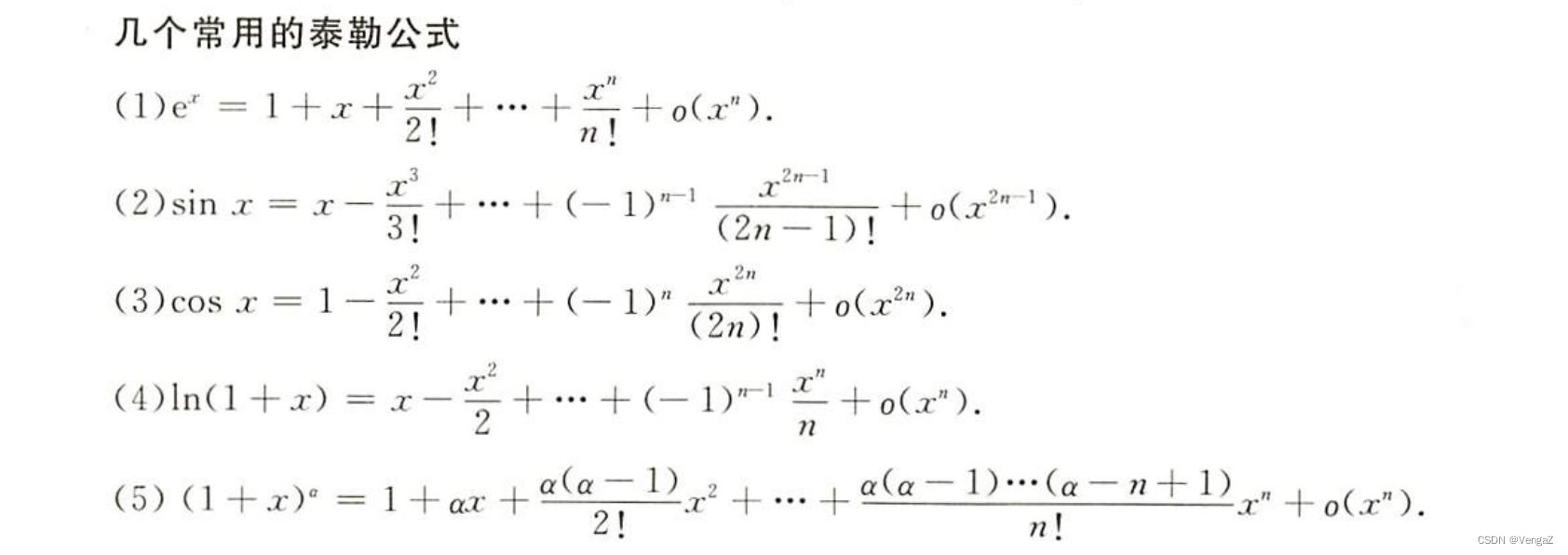
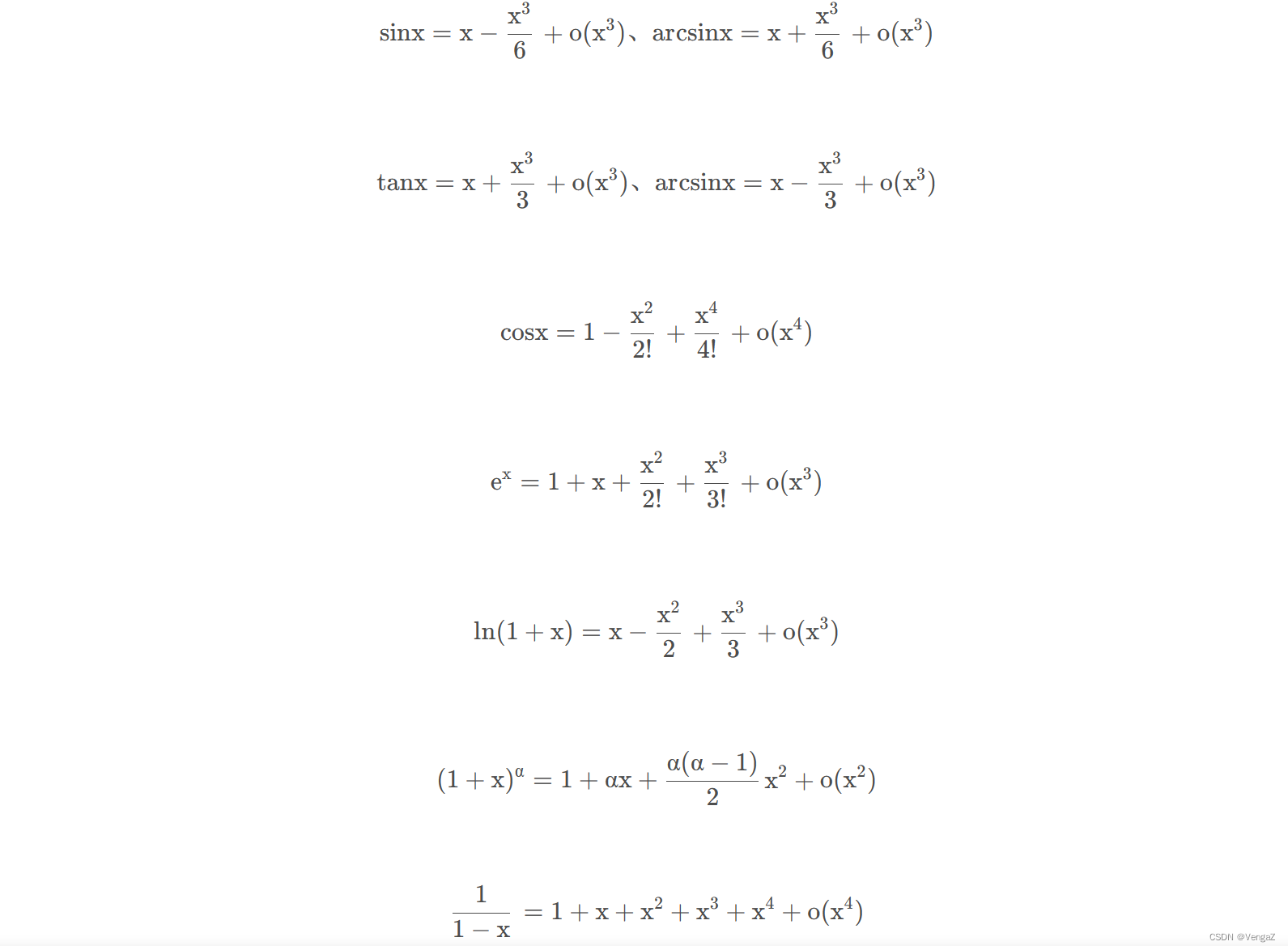
例78（展开到跟分母一样就行，超过也是等价无穷小）

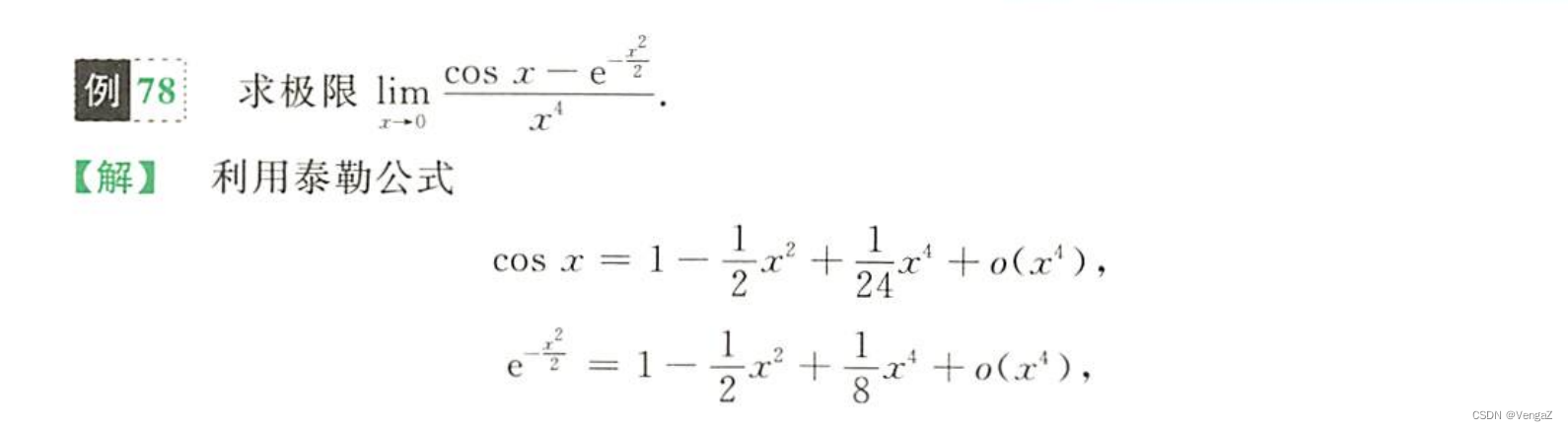
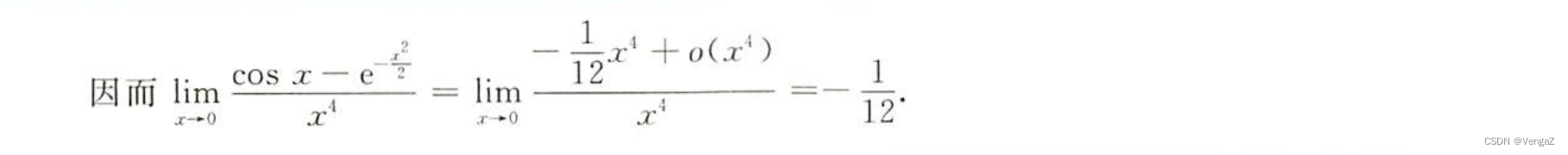
例79 （很妙，凑等价，与分母同阶）

例80（法二需要注意函数连续性的）

二阶可导不能说明二阶导连续只能说明一阶导连续，原函数连续

（10）求极限的其他方法

总结

在高等数学中，求极限是一个重要的概念和技巧，它在微积分和数学分析等领域中经常被应用。以下是几种常见的求极限的方法：

1. 代数运算法：通过对极限表达式进行代数运算，化简或转化成已知的极限形式，从而求解极限。这包括利用基本代数运算规则、因式分解、有理化等方法进行变形，使得极限的计算更加简化。

2. 夹逼定理（夹挤定理）：夹逼定理是一种常用的求极限方法，它基于一个原理：如果一个函数在某一点的左右两侧有两个函数夹住，并且这两个函数的极限都存在且相等，那么原函数在该点的极限也存在且等于夹逼的极限。通过找到比较简单的上下界函数，将待求的极限夹在它们之间，可以推导出原函数的极限。

3. 极限的基本性质和公式：在高数中有许多常见的极限性质和公式，例如极限的四则运算、极限的乘法法则、幂函数极限、指数函数极限、三角函数极限等。利用这些基本性质和公式，可以直接计算出许多常见函数的极限。

4. 利用洛必达法则（L’Hôpital’s rule）：洛必达法则是一种用于求解不定型（形如0/0或∞/∞）极限的重要工具。它通过对函数的分子和分母同时求导，并计算导数的极限，来求解原函数的极限。洛必达法则适用于求解形如0/0或∞/∞的极限，但需要注意其使用条件和假设。

5. 泰勒展开（Taylor expansion）：泰勒展开是一种利用函数的无穷次导数来逼近函数的方法。通过将函数展开成幂级数，可以近似计算函数在某一点的极限。泰勒展开在计算复杂函数的极限时非常有用，尤其是在使用其他方法求解困难的极限时。

需要注意的是，不同的极限问题可能需要使用不同的方法来求解。在实际应用中，选择合适的方法往往需要对问题进行分析和判断。熟练掌握这些方法，结合具体问题的特点，可以更有效地求解高等数学中的极限。