目录
- 移动零
- 复写零
- 快乐数
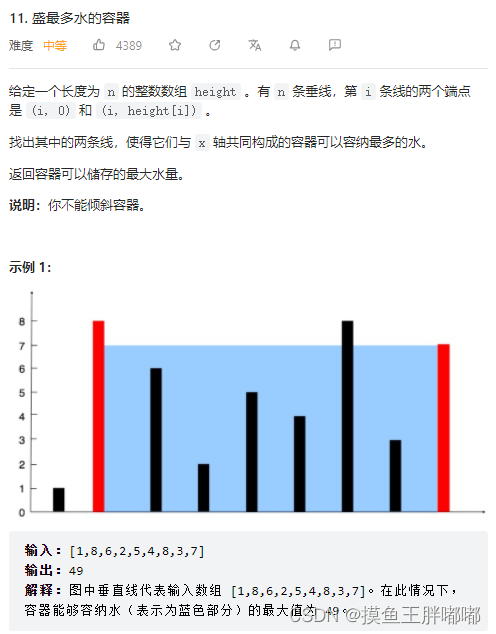
- 盛最多水的容器
- 有效三角形的个数
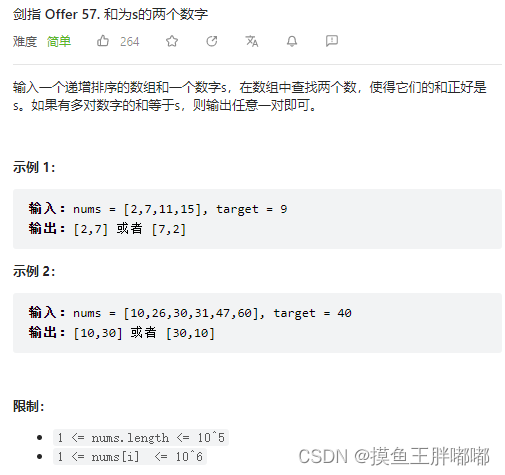
- 和为s的两个数
- 三数之和
- 四数之和
移动零
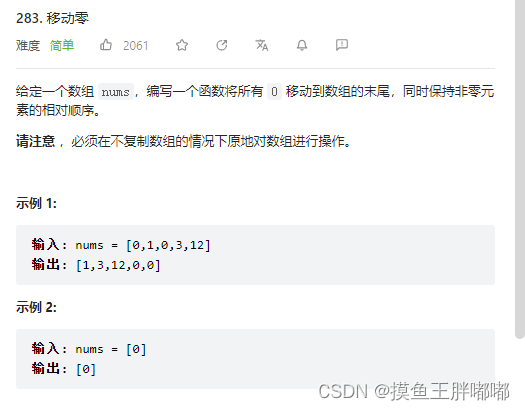
算法原理:
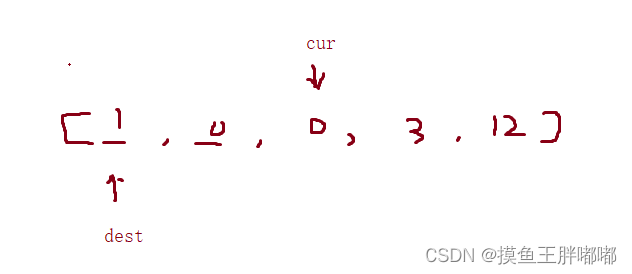
数组划分(数组分块)
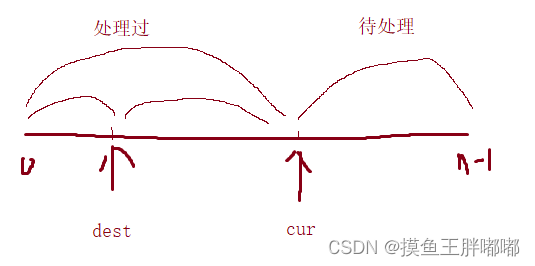
两个指针作用:
cur:从左到右扫描数组,遍历数组
dest:已处理的区间内,非零元素的最后一个位置
三个区间:
[0.dest]:已经处理过的非零元素
[dest+1, cur-1]:处理过的零元素
[cur,n-1] :待处理元素
情况1:当cur遇到0元素的时候,直接让cur向后移动一位
情况2:当cur遇到非零元素的时候,dest往后一位。然后交换这两个位置的元素,然后cur+1
情况3:当cur遍历到n时,就完成了区间的划分
总结:
cur从前往后遍历的过程中:
1.遇到0元素:cur元素++
2.遇到非零元素:
swap(dest+1,cur);
dest++,cur++;
代码
class Solution {
public void moveZeroes(int[] nums) {
for(int cur = 0, dest = -1; cur < nums.length; cur++) {
if(nums[cur] != 0) {
dest++;
int tmp = nums[cur];
nums[cur] = nums[dest];
nums[dest] = tmp;
}
}
}
}
复写零
算法原理:
解法:双指针算法
先根据“异地”操作,然后优化成双指针下的“就地”操作
异地操作就是说开辟一个新的数组,定义一个指针指向原始数组,定义一个新指针指向新数组,然后进行操作。
就地操作,就是把两个指针定义在同一个数组上。
1.先找到最后一个“复写”的数;
双指针算法:
1)先判断cur位置的值
2)决定dest向后移动一步或者两步
3.)判断一下dest是否已经到结束为止
4)cur++
1.5. 处理一下边界情况
n-1 -> 0
cur–
dest -=2
2.“从后向前”完成复写操作;
代码
public static void duplicateZeros(int[] arr) {
int cur = 0, dest = -1, n = arr.length;
// 1. 先找到最后一个需要复写的数
while (cur < n) {
if (arr[cur] == 0) dest += 2;
else dest += 1;
if (dest >= n - 1) break;
cur++;
}
// 1.5 处理一下边界情况
if (dest == n) {
arr[n - 1] = 0;
cur--;
dest -= 2;
}
// 2. 从后向前完成复写操作
while (cur >= 0) {
if (arr[cur] != 0) arr[dest--] = arr[cur--];
else {
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}
快乐数

算法原理:
判断链表是否有环
解法:快慢双指针
1.定义快慢指针
2.慢指针每次向后移动一步,快指针每次向后移动两步
3.判断相遇时候的值即可
代码
class Solution {
public int bitSum(int n) { // 返回n这个数每一位上的平方和
int sum = 0;
while (n != 0) {
int t = n % 10;
sum += t * t;
n /= 10;
}
return sum;
}
public boolean isHappy(int n) {
int slow = n;
int fast = bitSum(n);
while (slow != fast) {
slow = bitSum(slow);
fast = bitSum(bitSum(fast));
}
return slow == 1;
}
}
盛最多水的容器
解法思路:
解法一:暴力枚举O(N^2)
解法二:利用单调性,使用双指针解决问题O(N)
代码
public int maxArea(int[] height) {
int left = 0;
int right = height.length - 1;
int ret = 0;
while (left < right) {
int v = Math.min(height[left], height[right]) * (right - left);
ret = Math.max(ret, v);
if (height[left] < height[right]) left++;
else right--;
}
return ret;
}
有效三角形的个数

算法原理:
利用单调性,使用双指针算法来解决问题
先对整个数组排序。
先固定最大的数
在最大的数的左区间内,使用双指针算法,快速统计出符合要求的三元组的个数
代码
import java.util.Arrays;
public class Solution {
public int triangleNumber(int[] nums) {
// 1. 优化:排序
Arrays.sort(nums);
// 2. 利用双指针解决问题
int ret = 0, n = nums.length;
for (int i = n - 1; i > 0; i--) {// 先固定最大的数
// 利用双指针快速统计出符合三元组的个数
int left = 0, right = i - 1;
while (left < right) {
if (nums[left] + nums[right] > nums[i]) {
ret += right - left;
right--;
} else {
left++;
}
}
}
return ret;
}
}
和为s的两个数
算法原理:
利用单调性,使用双指针算法解决问题
代码
public int[] twoSum(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum > target) right--;
else if (sum < target) left++;
else return new int[]{nums[left], nums[right]};
}
// 照顾编译器
return new int[]{0};
}
三数之和

算法原理:
排序+双指针
1.排序;
2.固定一个数i
3.在该数后面的区间内,利用“双指针算法”,快速找到两个的和等于-i即可
处理细节:
1.去重 :找到一种结果之后,left和right指针要跳过重复元素;当使用完一次双指针算法之后,i也需要跳过重复元素
2.不漏 : 找到一种结果之后,不要”停“,缩小区间,继续寻找
代码
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ret = new ArrayList<>();
// 1. 排序
Arrays.sort(nums);
// 2. 利于双指针解决问题
int n = nums.length;
for (int i = 0; i < n;) {//固定数 a
if (nums[i] > 0) break;// 小优化
int left = i + 1;
int right = n - 1, target = -nums[i];
while (left < right) {
int sum = nums[left] + nums[right];
if (sum > target) right--;
else if (sum < target) left++;
else {
// nums[i] nums[left] nums[right]
ret.add(new ArrayList<Integer>(Arrays.asList(nums[i], nums[left], nums[right])));
// 缩小区间,继续寻找
left++;
right--;
// 去重
while (left < right && nums[left] == nums[left - 1]) {
left++;
}
while (left < right && nums[right] == nums[right + 1]) {
right--;
}
}
}
// 去重: i
i++;
while (i < n && nums[i] == nums[i - 1]) i++;
}
return ret;
}
}
四数之和

算法原理:
排序+双指针
1.依次固定一个数a;
2.在a后面的区间内,利用“三数之和“找到三个数,使这三个数的和等于 target-a即可
代码
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> ret = new ArrayList<>();
// 1. 排序
Arrays.sort(nums);
// 2. 利用双指针解决问题
int n = nums.length;
for (int i = 0; i < n; ) {// 固定数a
// 三数之和
for (int j = i + 1; j < n; ) {// 固定数 b
// 双指针
int left = j + 1, right = n - 1;
long aim = (long)target - nums[i] - nums[j];
while (left < right) {
int sum = nums[left] + nums[right];
if (sum > aim) right--;
else if (sum < aim) left++;
else {
ret.add(Arrays.asList(nums[i], nums[j], nums[left++], nums[right--]));
// 去重一
while (left < right && nums[left] == nums[left - 1]) left++;
while (left < right && nums[right] == nums[right + 1]) right--;
}
}
// 去重二
j++;
while (j < n && nums[j] == nums[j - 1]) j++;
}
// 去重三
i++;
while (i < n && nums[i] == nums[i - 1]) i++;
}
return ret;
}
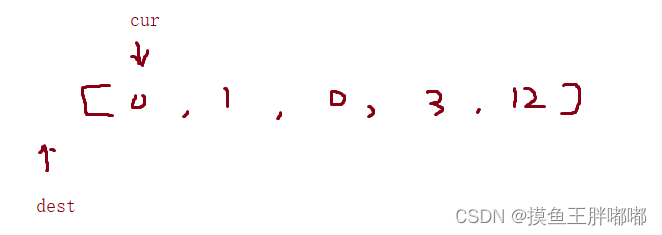
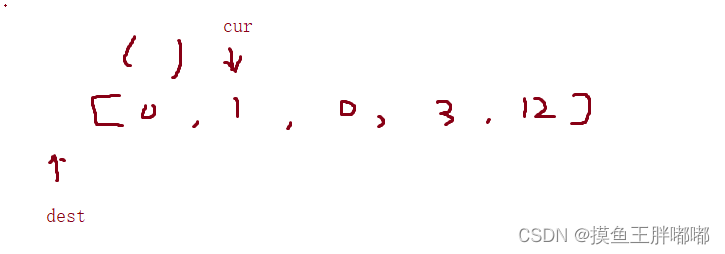
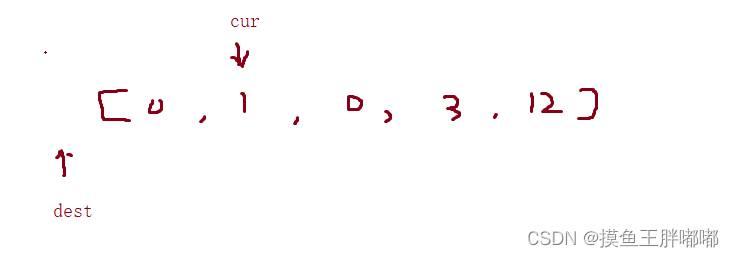
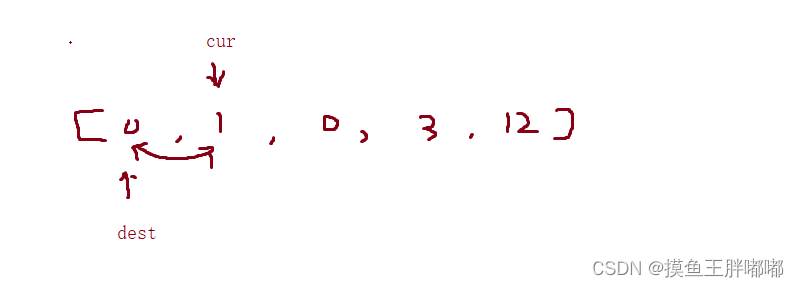





![[QT编程系列-10]:C++图形用户界面编程,QT框架快速入门培训 - 4- QT画图与动画](https://img-blog.csdnimg.cn/044315a8acd542b5a329c6b48c09381d.png)