【精讲】高等数学中的数列极限解析

博主：命运之光的主页

专栏：高等数学

目录

导言

一、数列极限的定义

二、数列极限的判定方法

三、数列极限的性质

必需记忆知识点 

 例题（用于熟悉数列极限）

例题1

例题2

例题3

结论

---

导言

 在高等数学中，数列极限是数学分析的重要概念之一。数列极限描述了数列随着项数的增加逐渐趋近于某个值或无穷大的性质。理解数列极限的概念和性质对于理解函数极限、级数以及微积分的基本思想至关重要。本文将详细讲解数列极限的定义、判定方法以及相关性质。

---

一、数列极限的定义

 给定一个数列{a_n}，其中每一项a_n表示数列中的第n个元素。如果存在一个实数L或正负无穷大，使得对于任意给定的ε（ε > 0），都存在一个正整数N，使得当n > N时，|a_n - L| < ε成立，则称数列{a_n}的极限为L。符号表示为lim(n→∞) a_n = L。

---

二、数列极限的判定方法

1. 数列极限的收敛与发散：

   • 如果一个数列存在有限极限L，则称该数列收敛。
   • 如果一个数列不存在有限极限，或者极限为正无穷大或负无穷大，则称该数列发散。

2. 数列极限的判定准则：

   • 夹逼准则：如果数列{a_n}、{b_n}和{c_n}满足对于所有的n，a_n ≤ b_n ≤ c_n，并且lim(n→∞) a_n = lim(n→∞) c_n = L，那么lim(n→∞) b_n = L。
   • 单调有界准则：如果数列{a_n}单调递增且有上界（或单调递减且有下界），则该数列收敛。
   • 零极限法则：如果一个数列的极限为0，而另一个数列的极限为有限数，则两个数列的极限乘积为0。

---

三、数列极限的性质

1. 数列极限的唯一性： 一个数列的极限（如果存在）是唯一的。

2. 数列极限的四则运算： 如果两个数列{a_n}和{b_n}的极限存在，则它们的和、差、乘积和商的极限也存在，并且满足如下性质：

   • lim(n→∞) (a_n + b_n) = lim(n→∞) a_n + lim(n→∞) b_n
   • lim(n→∞) (a_n - b_n) = lim(n→∞) a_n - lim(n→∞) b_n
   • lim(n→∞) (a_n * b_n) = lim(n→∞) a_n * lim(n→∞) b_n
   • lim(n→∞) (a_n / b_n) = (lim(n→∞) a_n) / (lim(n→∞) b_n) （假设lim(n→∞) b_n ≠ 0）

---

必需记忆知识点 

---

 例题（用于熟悉数列极限）

例题1

---

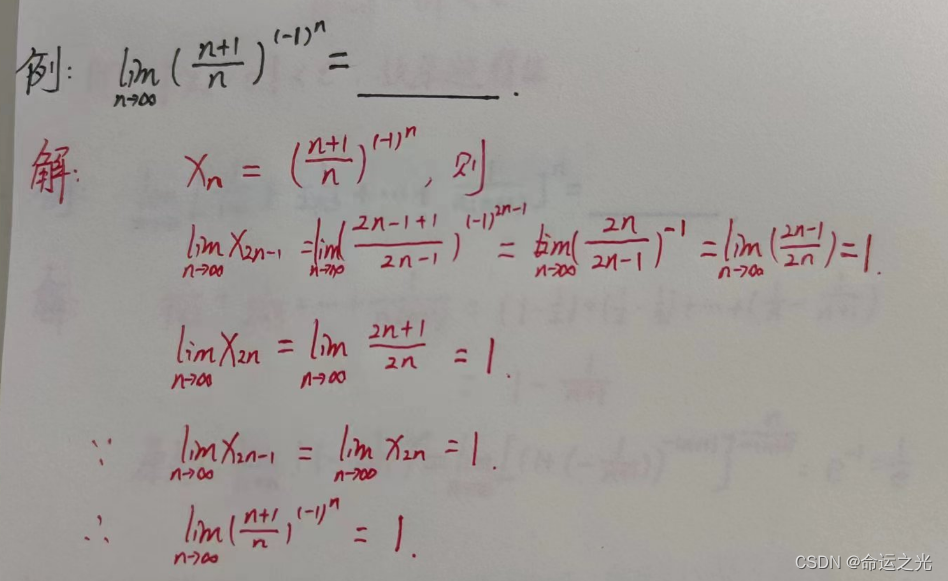
例题2

---

例题3

---

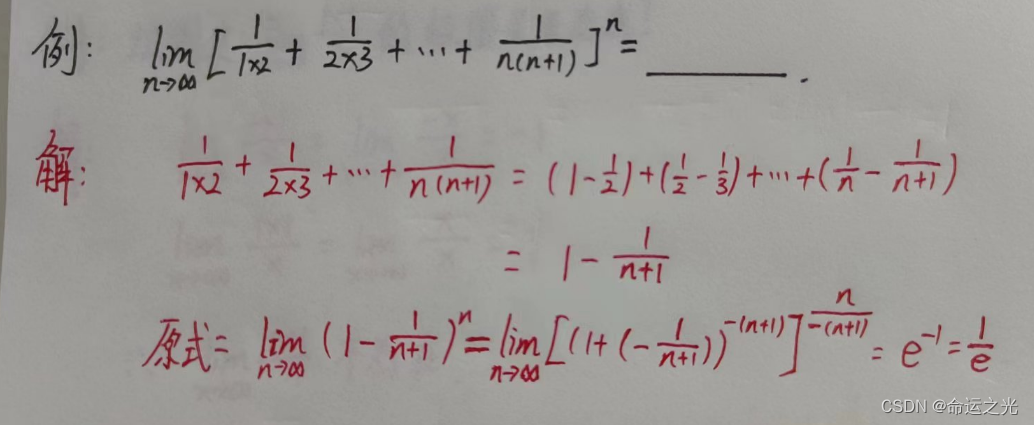
结论

数列极限是数学分析中的重要概念，描述了数列逐渐趋近于某个值或无穷大的性质。数列极限的判定方法包括夹逼准则、单调有界准则和零极限法则。数列极限具有唯一性和满足四则运算的性质。深入理解数列极限的概念和性质对于理解函数极限、级数以及微积分的基本思想至关重要。

---

本章的内容就到这里了，觉得对你有帮助的话就支持一下博主把~

🌌点击下方个人名片，交流会更方便哦~
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓