题目

给你一个有 n 个结点的二叉树的根结点 root ，其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点，或者从子结点移动到父结点。

返回使每个结点上只有一枚硬币所需的最少移动次数。

示例 1：
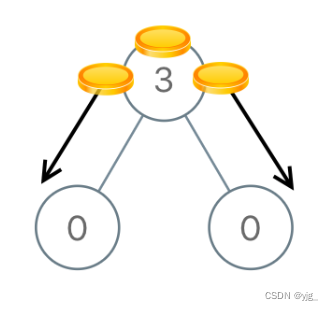
在这里插入图片描述

输入：root = [3,0,0]
输出：2
解释：一枚硬币从根结点移动到左子结点，一枚硬币从根结点移动到右子结点。

树中节点的数目为 n
1 <= n <= 100
0 <= Node.val <= n
所有 Node.val 的值之和是 n

一题一解：DFS(java)

思路

我们要寻找每个节点判断是否，有多余的或者不足的硬币，如果有此时我们应该给答案加上差值，因为不足和多余都是要移动硬币的情况，所以对于答案来说，视为一种情况，都为加在答案ans上。

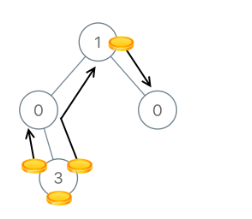
步骤解析

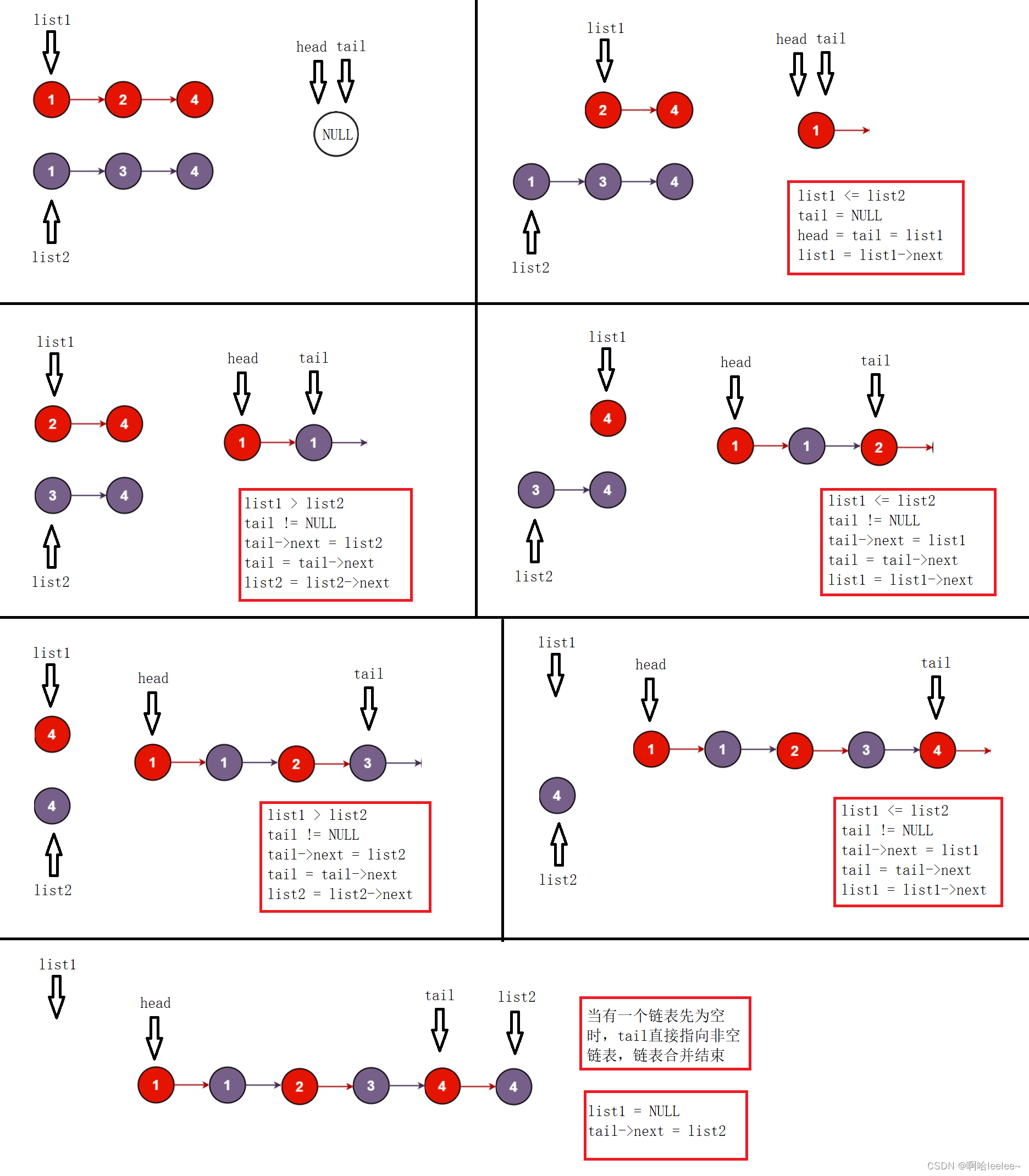
我们从根节点开始遍历，如上图所示，
值为3的父节点因为没有左节点所以，左节点返回的数组是int []{0,0};

当我们遍历到右节点值为3的时候，在往下遍历时候，值为3的节点是没有左右节点的所以，值为3节点返回的数组int[]{coins,nodes}是int[]{3,1} 那么答案经过计算ans+=Math.abs(coins-nodes);值就为2。

那么值为3的父节点，返回的数组是以它所形成子树的硬币数和节点数总值，
int[]{3,2} ,那么答案经过计算,值就为3

其实叶子节点也就看作了是子树，只是特殊的子树，返回的还是以叶子节点所形成的子树总的硬币数和节点数。

那么返回给它的父节点也就是返回给值为1的节点，它左节点返回的是int[]{3,2}，当遍历它右节点的时候，因为右节点是叶子节点且没有值，所以它所形成的子树总的硬币coins=0，节点node=1，返回数组为int[]{0,1},那么答案经过计算,值就为4。
所以根节点的左节点形成的子树返回的是int[]{3,2}，右节点形成的子树返回的是int[]{0,1},根节点计算之后，coins=3，nodes=3，答案ans不用变化。所以结果是4

测试代码


class Solution{
    private  int ans=0;
    public int distributeCoins(TreeNode root) {
        dfs(root);
        return ans;
    }
   private int[]  dfs(TreeNode treeNode){
        //当走到叶子节点的时候左右节点所形成的子树没有值
        if (treeNode==null)return new int[]{0,0};
        //遍历当前节点的左节点，返回当前左节点所形成的子树的硬币数和节点数
        int[] left=dfs(treeNode.left);
       //遍历当前节点的右节点，返回当前右节点所形成的子树的硬币数和节点数
        int[] right=dfs(treeNode.right);
        //计算当前节点的总硬币数
        int coins=left[0]+right[0]+treeNode.val;
       //计算当前节点的总节点数
        int nodes=left[1]+right[1]+1;
        //计算当前节点要移动多少个硬币给父节点或者从父节点拿入硬币
        ans+=Math.abs(coins-nodes);
        return new int[]{coins,nodes};
    }
}

复杂度分析

时间复杂度:O(n)，n为二叉树的节点个数。
空间复杂度:O(h)。h为二叉树的高度。

运行结果

优化代码

思路

在函数dfs(node)中，我们首先遍历左右子树，获得左右子树的是有多余的还不足的硬币数量left和right。那么答案ans需要加上|left| + |right|表示左右子树硬币移动的次数，也就是说左右子树中的金币移动到他们的父节点次数。然后，返回当前节点也就是左右子树的父节点所形成的整个子树的硬币是多余的量还是不足的量，也就是加上左右子树的多余的量还是不足的量再加上当前节点硬币的数量减去减去自己一个节点数。left +right+node.val - 1。直到根节点。

测试代码

class Solution{
    private  int ans=0;
    public int distributeCoins(TreeNode root) {
        dfs(root);
        return ans;
    }
    private int dfs(TreeNode treeNode){
        if (treeNode==null)return 0;

        int left=dfs(treeNode.left);
        int right=dfs(treeNode.right);

        ans+=Math.abs(left)+Math.abs(right);

        return left+right+treeNode.val-1;
    }
}