问题链接: AcWing 107. 超快速排序

问题描述

分析
这道题考查的算法不难，就只是利用归并排序来求逆序对的数量，但是主要是如何分析问题，如何能从问题中看出来和逆序对数量有关，现在的题目基本上很少是那种模板算法题了，更注重思维，所以一定要培养好思维，模板只是基础。

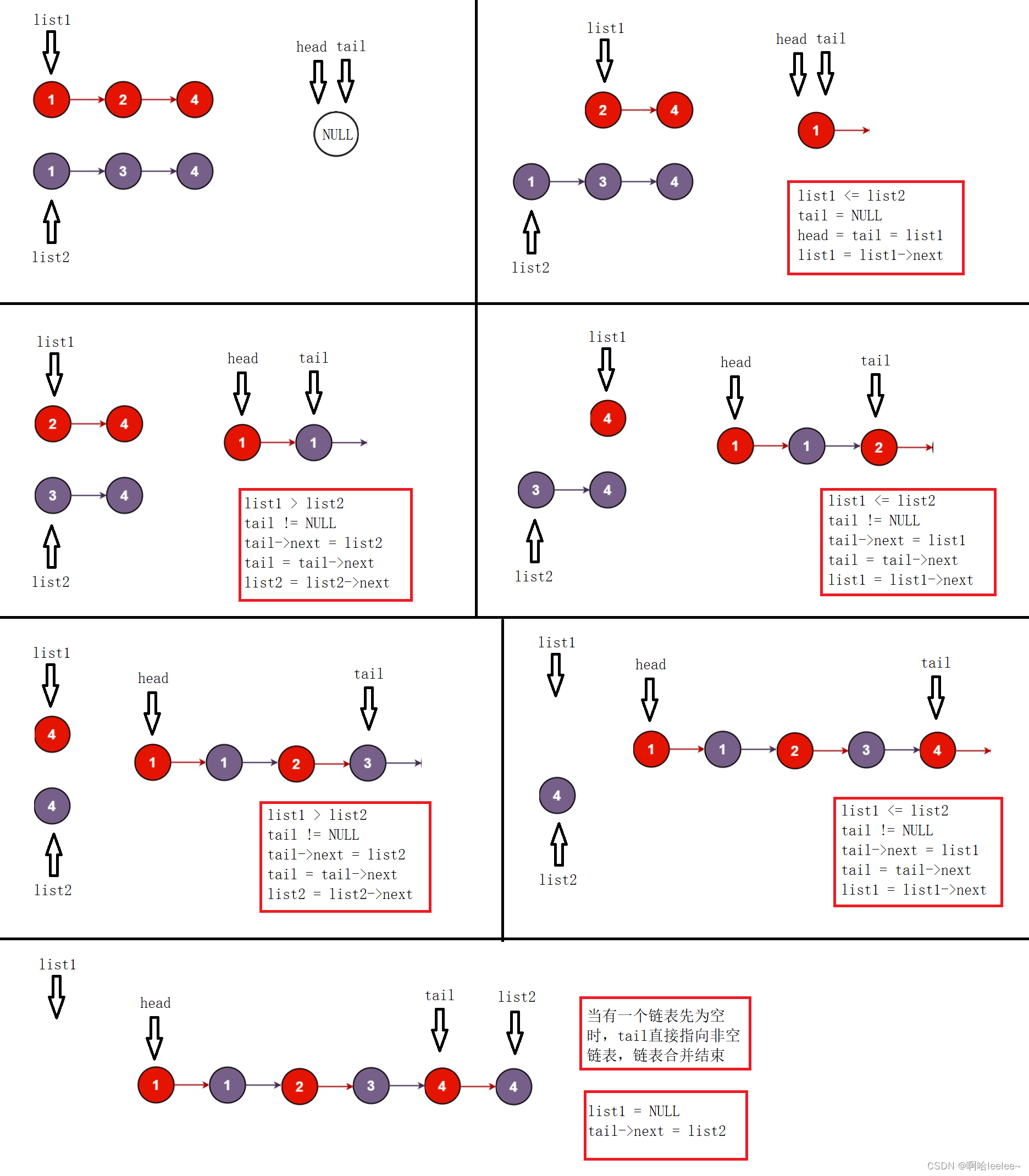
这道题交换相邻的两个数，首先会先想到冒泡排序，冒泡排序就是交换相邻的两个数，这道题用冒泡排序也能做，但是冒泡排序时间复杂度是$O(n^2)$的，肯定过不了。我们思考冒泡排序在什么情况下会交换两个相邻的数，目标是升序序列时，当f[i]>f[i+1]时，会交换f[i]与f[i+1]，交换后可以发现f[i]的逆序对数量减少了一个，所以就能往这方面想，最后可以发现逆序对的数量就是需要交换的最少次数。

思维很重要，或者说在熟知算法模板的情况下，更重要的就是思维了。
代码如下

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=5e5+10;

ll f[N];
ll tmp[N];
ll n,k;
void merge_sort(int l,int r){
    if(l>=r) return;
    int mid=l+r>>1;
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    int i=l,j=mid+1,t=0;
    while(i<=mid&&j<=r)
        if(f[i]<=f[j]) tmp[t++]=f[i++];
        else{
            tmp[t++]=f[j++];
            k+=mid-i+1;
        } 
    while(i<=mid) tmp[t++]=f[i++];
    while(j<=r) tmp[t++]=f[j++];
     
    for(int i=l;i<=r;i++) f[i]=tmp[i-l];
}
int main(){
    while(~scanf("%d",&n)&&n){
        for(int i=0;i<n;i++) scanf("%lld",&f[i]);
        k=0;
        merge_sort(0,n-1);
        printf("%lld\n",k);
    }
    return 0;
}