目录
FIR 滤波器去除噪声
解决方案一：滑动平均滤波方法
解决方案二：另外一种理解角度-----引入权重系数概念
FIR滤波器表达式
FIR滤波器
一、FIR滤波器的基本结构
二、FIR滤波器的设计方法
1、频率采样法
2、窗函数法
三、FIR滤波器的性能指标
1、通带衰减（Passband Attenuation）
2、阻带衰减（Stopband Attenuation）
3、过渡带宽（Transition Bandwidth）
4、群延迟（Group Delay）
四、FIR滤波器的应用
1、音频处理
2、图像处理
3、视频处理
4、通信系统
五、总结
FIR 滤波器去除噪声
=====以下来自知乎：https://www.zhihu.com/question/323353814/answer/2708545913======
仿真生成了两段信号。其中一条是未加入噪声的纯净信号，另外一条是加入白噪声后的含噪声信号。其中纯净信号使用了一段正弦信号。我们的目的就是将含噪声信号中的噪声部分滤除，得到一条尽量还原纯净信号的滤波结果。
解决方案一：滑动平均滤波方法
从上图容易看出，含噪声信号是在纯净信号上下波动的，所以很容易想到，如果取某几个含噪声信号的平均值，作为滤波结果，则可以抵消掉噪声在上下随机波动中的干扰效果。假如我们每3个点做一次平均，实现过程见下图（为了便于观察，使用前0.25秒数据演示）：
图2. 每三个红点求平均得到一个蓝点
能够看出，经过该方法处理后的数据相对于纯净信号的波动幅值得到了一定程度的抑制，也就是可以取得一定程度的滤波效果。
这是一种最简单的FIR滤波器，也可以叫做滑动平均滤波方法。
解决方案二：另外一种理解角度-----引入权重系数概念
上边讲到的滑动平均，是将3个相邻信号求取平均值，这也可以理解为这3个值分别乘以权重系数1/3再求和，那么上述滤波过程可以用下边这张动图来演示，应该是比较直观的了：
图3. 选取了前10个数据点作为演示
FIR滤波就是在时域上卷积的过程。
卷积有一个重要性质：时域的卷积等于频域相乘。
这个性质可以说和滤波是息息相关的，因为滤波的目的就是想要得到某特定的频率段。而频域相乘恰恰能够实现这个筛选的目的。
回到文章最开始的例子，想要对含噪声信号滤波，那我们不妨先看看他的频谱：
可以看到我们想要保留的频率段范围基本在3Hz以下，高于3Hz的都可以抛弃，很自然地，我们可以想到一个办法，即构造如下一组频域信号：
此时将图11中的频谱和图12相乘，高于3Hz的数值就全部变为了0，此时频谱就成了：
再将此频域数值进行傅里叶逆变换，得到时域数值：
可以看到我们近乎完美的实现了滤波。一句话表述上述滤波过程：设计一个频域滤波器（将想要保留的频率段赋值为1，其他频率段赋值为0），将其与含噪声信号的频谱在频域上相乘，再将乘积做傅里叶逆变换，即可实现滤波，这种滤波器叫频域滤波器。
虽然得到了较好的滤波结果，但是事情到这里还没完，不要忘记这篇文章是讲FIR滤波器的~
注意看上边那段话中的加黑字体：在频域上相乘。回想起来了吗？
时域的卷积等于频域相乘！
所以，上述在频域空间的一大堆操作，可以简单地转化成在时域上的卷积操作，具体来说，就是将含噪声信号与低通滤波器的傅里叶逆变换值进行卷积，这个过程就是FIR滤波。
我用一张图表示他们之间的关系：
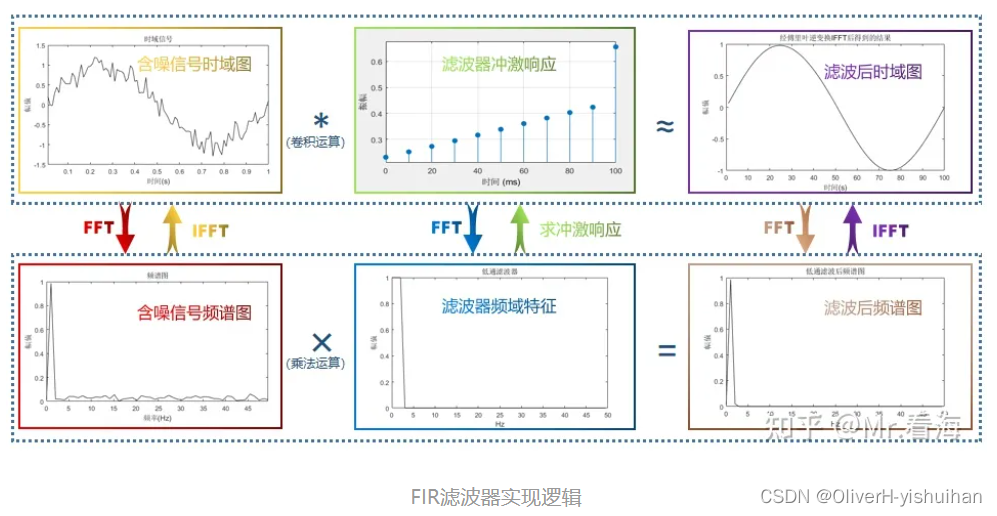到这里你应该已经理解了，FIR滤波器的本质是设计一组系数，这组系数实际就是滤波器的IFFT（冲激响应，还记得张三的鼓包吗）离散化以后的结果。
FIR滤波器表达式
将上述的理论浓缩成一个表达式，表示FIR滤波器：
y[n]=a0x[n]+a1x[n−1]+a2x[n−2]+...y[n]=a_0x[n]+a_1x[n-1]+a_2x[n-2]+...
上式中的 x代表待滤波数据，y代表输出数据；系数a0、a1、a2...就是滤波器的冲激响应系数。所以在 FIR滤波器中，每一时刻的输出取决于之前的有限个输入，因此就是“有限冲激响应”。
=====以上来自知乎：https://www.zhihu.com/question/323353814/answer/2708545913======
什么是FIR滤波器，FIR滤波器的基本结构、设计方法、性能指标以及应用-芯三七 (ic37.com)
FIR滤波器
FIR滤波器是一种数字滤波器，用于对数字信号进行滤波处理。FIR是Finite Impulse Response的缩写，中文翻译为有限脉冲响应滤波器。FIR滤波器的特点是具有线性相位和稳定性，适用于低通、高通、带通和带阻等各种滤波器设计。
一、FIR滤波器的基本结构
FIR滤波器的基本结构由一组加法器和一组乘法器组成，也被称为“移动平均滤波器”。
FIR滤波器的输入信号通过一系列的乘法器和加法器进行处理，输出信号的值是输入信号和一组系数的线性组合。这些系数也被称为滤波器的“权值”，它们决定了滤波器的特性和性能。
FIR滤波器的基本结构是一个有限长的序列，其输出信号只依赖于当前和前面的输入信号，而不依赖于未来的输入信号。这种结构可以用一个线性方程组表示，其中系数矩阵是对称矩阵，因此FIR滤波器也被称为“线性相位滤波器”。
FIR滤波器具有许多优点，如稳定性、易于设计和实现、通带和阻带特性易于控制等。它们广泛应用于数字信号处理中，如音频处理、图像处理、通信系统等。
二、FIR滤波器的设计方法
FIR滤波器的设计方法有两种：频率采样法和窗函数法。
1、频率采样法
频率采样法是一种基于频域设计的方法，首先根据滤波器的频率响应要求，确定滤波器的通带、阻带和过渡带宽等参数。然后，将这些参数转换成频率采样点对应的幅度响应值，即滤波器的理想频率响应。最后，通过反变换得到滤波器的时域系数。
具体步骤如下：
- （1）根据滤波器的通带、阻带、过渡带等参数，确定滤波器的理想频率响应Hd(ω)。
- （2）将频率采样点ωk对应的幅度响应值Hd(ωk)求出。
- （3）通过反变换得到滤波器的时域系数h(n)。
频率采样法的优点是设计简单，容易理解和实现，但是对于一些特殊的滤波器要求，如阶数较高、过渡带较窄等，可能会出现频率取样误差和幅度失真的问题。
2、窗函数法
窗函数法是一种基于时域设计的方法，通过选择合适的窗函数来实现滤波器的设计。窗函数是一种在时域上截断信号的函数，将信号变成有限长度的信号。窗函数的选择会影响滤波器的频率响应和深度。
具体步骤如下：
- （1）根据滤波器的通带、阻带、过渡带等参数，确定滤波器的理想频率响应Hd(ω)。
- （2）选择窗函数W(n)。
- （3）计算截断信号h(n)与窗函数W(n)的卷积，得到滤波器的时域系数。
- （4）对滤波器进行归一化处理。
窗函数法的优点是设计灵活，可以根据不同的滤波器要求选择不同的窗函数，但是窗函数的选择和截断会影响滤波器的频率响应和深度。
三、FIR滤波器的性能指标
FIR滤波器的性能指标主要包括以下几个方面：
1、通带衰减（Passband Attenuation）
通带衰减是指在滤波器的通带内，滤波器对信号的衰减程度，通常用分贝（dB）来表示。通带衰减越小，滤波器在通带内的输出信号幅度衰减越小，滤波器的通带增益越大。
2、阻带衰减（Stopband Attenuation）
阻带衰减是指在滤波器的阻带内，滤波器对信号的衰减程度，通常用分贝（dB）来表示。阻带衰减越大，滤波器对阻带内的干扰信号和噪声的抑制能力越强。
3、过渡带宽（Transition Bandwidth）
过渡带宽是指滤波器从通带到阻带的过渡段的带宽，通常用Hz或π单位来表示。过渡带宽越小，滤波器的频率响应变化越陡峭，滤波器的过渡段越短。
4、群延迟（Group Delay）
群延迟是指滤波器在不同频率处的信号延迟时间，通常用秒或样点单位来表示。群延迟越小，滤波器对信号的时间延迟越小，对信号的畸变程度越小。
四、FIR滤波器的应用
FIR滤波器具有许多应用，包括音频处理、图像处理、视频处理、通信系统等。以下是几个典型的应用场景：
1、音频处理
FIR滤波器在音频处理中有广泛应用，如在音频均衡器、音频压缩器和音频限幅器等中。通过对音频信号进行滤波处理，可以改善音质、降低噪音和增强音效。
2、图像处理
FIR滤波器在图像处理中也有广泛应用，如在图像增强、去噪和边缘检测等中。通过对图像信号进行滤波处理，可以改善图像质量、降低噪声和增强边缘信息。
3、视频处理
FIR滤波器在视频处理中也有广泛应用，如在视频编码、视频压缩和视频增强等中。通过对视频信号进行滤波处理，可以提高视频质量、减少数据量和增强视觉效果。
4、通信系统
FIR滤波器在通信系统中也有广泛应用，如在数字调制解调器、频率合成器和数字滤波器等中。通过对通信信号进行滤波处理，可以降低噪声、提高信噪比和增强信号质量。
五、总结
FIR滤波器是一种基于时域设计的数字滤波器，具有线性相位和稳定性，适用于低通、高通、带通和带阻等各种滤波器设计。FIR滤波器的设计方法有频率采样法和窗函数法，其性能指标包括通带衰减、阻带衰减、过渡带宽和群延迟等。FIR滤波器在音频处理、图像处理、视频处理和通信系统等领域都有广泛应用。
