在伺服系统选型及调试中，刚性、惯量、响应时间及伺服增益调整之间的关系错综复杂，这些因素在控制系统中相互影响，对于系统的稳定性和性能至关重要。但在实践中如何调整取值比较合理，这些就算是工程师都会经常感到困惑。所以了解它们之间的相互关系可以帮助我们更好地优化和调整系统。

刚性、惯量、响应时间和伺服增益调整之间存在密切的关系。惯量和刚性影响系统的响应时间和稳定性，而伺服增益调整可以通过改变系统的响应特性来满足控制需求。

01.刚性

刚性是指物体坚硬受力时不易发生形变，对于一个结构固定的物体，刚性是其固有的特性。

说起“刚性”，就必须提到“刚度”，刚度是指材料或结构在受力时抵抗弹性变形的能力，是材料或结构弹性变形难易程度的表征。

比如，我们知道钢管比较坚硬，一般受外力形变小，而橡皮筋比较软，受到同等力产生的形变就比较大，那我们就说钢管的刚性强，橡皮筋的刚性弱，或者说其柔性强。

任何物体在受外力作用时都会发生形变，但如果形变的程度相对于物体本身线度来说极为微小或者物体的形变不影响所研究的问题时，就可将形变忽略不计，把物体视为刚体。

所以，在伺服系统中，用联轴器来连接电机和负载，可以看作是刚性连接；而用同步带或者皮带来连接电机和负载，可以看作是柔性连接。

电机刚性就是电机轴抗外界力矩干扰的能力，我们可以在伺服控制器中调节电机的刚性。

伺服电机的机械刚度跟它的响应速度有关。一般刚性越高其响应速度也越高，但是调太高的话，很容易让电机产生机械共振。所以，在一般的伺服参数里面都有手动调整响应频率的选项，要根据机械的共振点来调整，需要时间和经验(其实就是调增益参数)。

在伺服系统位置模式下，施加力让电机偏转，如果用力较大且偏转角度较小，那么就认为伺服系统刚性强，反之则认为伺服刚性弱。注意这里我说的刚性，其实更接近响应速度这个概念。从控制器角度看的话，刚性其实是速度环、位置环和时间积分常数组合成的一个参数，它的大小决定机械的一个响应速度。

其实如果你不要求定位快，只要准，在阻力不大的时候，刚性低，也可以做到定位准，只不过定位时间长。因为刚性低的话定位慢，在要求响应快，定位时间短的情况下，就会有定位不准的错觉。

02.惯量

惯量描述的是物体运动的惯性，是物体的固有特性，转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度，用字母I或J表示。

转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形象地理解为一个物体对于旋转运动的惯性。

转动惯量只跟转动半径和物体质量有关。一般负载惯量超过电机转子惯量的10倍，可以认为惯量较大。

(1)转动惯量计算公式为：

其中J是转动惯量， 表示刚体的某个质点的质量，表示该质点到转轴的垂直距离。

常见刚体的转动惯量

(2)转动惯量和力矩的关系为：

M=Jβ

其中M是扭转力矩，J是转动惯量，β是角加速度。

由上式中，角加速度(β)越大，所需要的力就越大；转动惯量(J)越大，所需要的力(M)也越大。

比如，在平稳运行当中，即角加速度(β)为零的时候，为克服转动惯量(J)而输出的力(M)就为零。

导轨和丝杠的转动惯量对伺服电机传动系统的刚性影响很大，固定增益下，转动惯量越大，刚性越大，越易引起电机抖动；转动惯量越小，刚性越小，电机越不易抖动。可通过更换较小直径的导轨和丝杆减小转动惯量从而减小负载惯量来达到电机不抖动。

在伺服系统选型及调试中，常会碰到伺服电机惯量匹配问题。

在伺服系统选型时，除考虑电机的扭矩和额定速度等等因素外，我们还需要先计算得知机械系统换算到电机轴的惯量，再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机。

惯量比与系统刚性和动态性能之间的关系图

在调试时，正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。此点在要求高速高精度的系统上表现尤为突出，这样，就有了惯量匹配的问题。

什么是“惯量匹配”呢？

进给轴的总惯量J＝伺服电机的旋转惯性动量JM ＋电机轴换算的负载惯性动量JL

负载惯量JL由（以平面金切机床为例）工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到电机轴上的惯量组成。

JM为伺服电机转子惯量，伺服电机选定后，此值就为定值，而JL则随工件等负载改变而变化。如果希望J变化率小些，则最好使JL所占比例小些。这就是通俗意义上的“惯量匹配”。

比如在有些用户的电机调试中遇到负载的转动惯量过大，导致调PID参数不起作用，该怎么解决呢？

这时可以考虑加装减速机，负载的转动惯量与减速比的平方成反比，且负载转动惯量最好应在电机转动惯量的15倍以内。

03.响应时间

响应时间可以理解为从指令发出到动作完成之间的时间。这里说的响应时间不需要以自控原理内讲的响应时间来标定，只作为一个定性的分析，可分为电气系统和机械系统。

(1)电气系统的响应时间，即给定一个位置、速度、转矩指令，到电机运行至该位置、速度、转矩的时间。

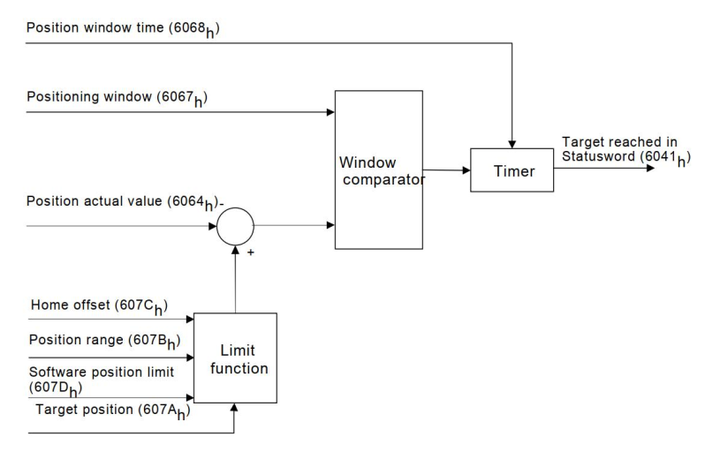
以位置模式为例，从控制系统发完指令到电机到达指定位置并停止所需要的时间即为响应时间，也可称为定位结束时间。

同样的，若给定一个速度、转矩指令，不给电机位置指令，电机会停在原位置上，但实际上电机并不是绝对静止的，而是在该位置上实现一个动态平衡。

此时，用一个外力，使电机偏离该位置，伺服系统会先检测到偏差，然后才会输出一个反向的力让电机回到原位置上去。

(2)机械的响应时间与机械的刚性和惯量是有直接关系的。

比如，如果用一根弹簧去拖动物体，我们知道弹簧的弹簧刚性弱，当指令(拉动距离)已经发出的时候，由于弹簧产生形变，被拖的物体还没有开始移动，而这个指令发出到物体到达指定位置的时间必然较长。

另一方面，对于一个固定大小的力，去转动某一个物体，根据公式M=Jβ，物体的转动惯量(J)越大，角加速度(β)就越小，到达指令转速的时间就越长。

04.伺服增益调整

首先，机械本身的结构对伺服增益的调整有重要影响。伺服驱动器包括三个反馈环节，即由内而外的电流环、速度环、位置环。

当我们在探讨整个机电系统响应性的时候，伺服速度、位置增益参数关系及总的调试思路是，最内环(电流环)的反应速度最快，中间环节(速度环)的反应速度必须高于最外环(位置环)。

如果不遵守此原则，将会造成电机运转的震动或反应不良。伺服驱动器的设计可尽量确保电流环具备良好的反应性能，故用户只需调整位置环、速度环的增益即可（以下增益调整以PMM系列一体化伺服电机为例,可参考通信手册https://wwwe.lanzoup.com/b0fewsjwb密码:cjtz）。

位置环的反应不能快于速度环的反应。因此，若需增加位置环的增益，必须先增加速度环的增益。如果只增加位置环的增益，电机很可能产生震动，从而将会造成速度指令及定位时间的增加，而非期望的减少。

可以假设机械系统是速度环的内环，如果机械本身的刚性比较好(联轴器传动)，伺服的相关增益则可以设置较高。如果机械本身的刚性偏柔(同步带)，伺服的相关增益则设置的不要太高。

(1)速度环增益

增大速度环比例增益，则能降低转速脉动的变化量，提高伺服驱动系统的硬度，保证系统稳态及瞬态运行时的性能。

但是在实际系统中，速度环比例增益不能过大，否则将引起整个伺服驱动系统震荡。速度环参数调节与负载惯量的关系当负载对象的转动惯量与电机的转动惯量之比较大，及负载的摩擦转矩比较大时，宜增大速度环比例增益和速度环积分时间常数，以满足运行稳定性的要求。

当负载对象的转动惯量与电动机的转动惯量之比较小，以及负载的摩擦转矩较小时，宜减小速度环比例增益和速度环积分时间常数，保证低速运行时的速度控制精度。

示例：

速度环（2008-01）增益设为880，速度环积分时间常数（2008-02）取个较大值，一般20-30ms，这里先取30ms。（如果大惯量负载，可以稍微放大一些）

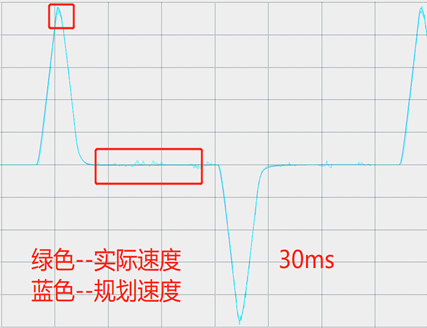
判断标准：运行时，实际速度(606C)和规划速度（606B）相同或者超调2%左右（如果减小，伺服振动，取振动时的积分时间常数上调100）。停止时，0速尽量不抖动（6044抖动不超过5rpm)。

(2)位置环增益

位置环增益与伺服电机以及机械负载有着密切的联系。

当伺服系统的位置环增益越高，电机速度对于位置指令响应的延时减少，位置跟踪误差愈小，定位所需时间越短，但要求对应的机械系统的刚性与自然频率较高。

而且当输入的位置突变时，其输出变化剧烈，机械负载要承受较大的冲击。此时，驱动器必须进行升降速处理或通过上位机用编程措施来缓冲这种变化。

当伺服系统位置环增益相对较小时，调整起来比较方便，因为位置环增益小，伺服系统容易稳定，对负载对象，调整要简单些。同时，低位置环增益的伺服系统频带较窄，对噪音不敏感。

因此，作为伺服进给时，位置的微观变化小，但位置环增益小的伺服系统位置跟踪误差较大，进行轮廓加工时，会在轨迹上形成加工误差。

示例：

位置环调试（速度环取880，1000）位置环增益（2008-03）逐渐 增大（200/500间隔）

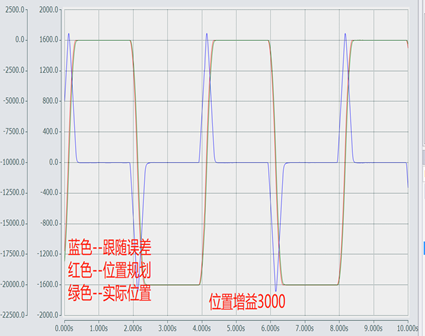
判断标准：实际位置（6063）不超调，跟随误差（60F4）2000以内。

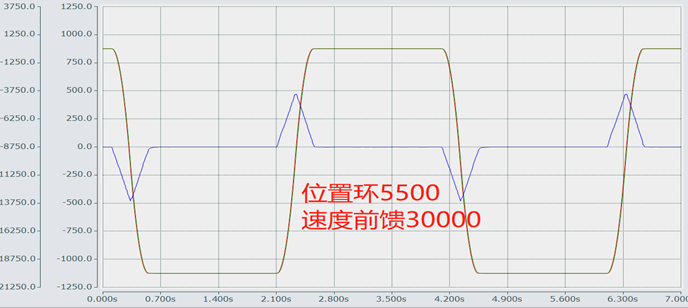
注：不同的加减速，跟随误差不一样，加减速减小，位置环增益需相应减小。

位置环增益根据实际跟随误差调整，如果加大位置环增益无明显改善，可以通过速度环前馈加以改善

伺服直接拖动丝杆测试（正反2圈，PP模式，T型加速，加减速120000rpm/s）

---

以上即是今天分享的全部内容，如果您有其他问题，请及时联系我们。

˜ 本文章全部内容或部分内容禁止擅自转载、拷贝。