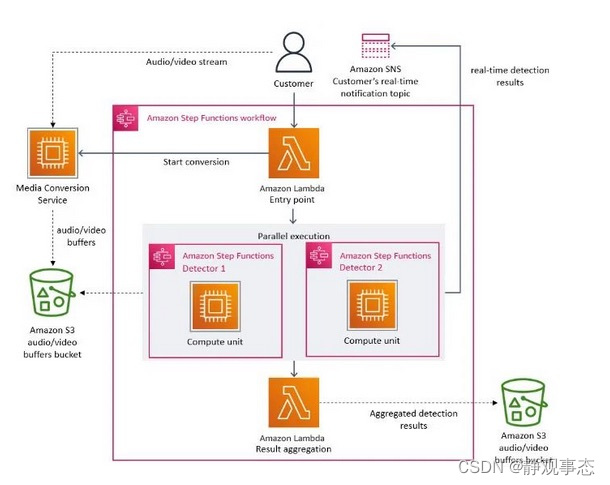
目录

本章学习重点：

        1：结构体类型的声明与变量的定义

        2：如何求解结构体的大小(结构体的内存对齐)

        3:结构体传参，结构体实现位段

        4：枚举类型的定义和优点

        5：联合的定义与特点及大小的计算

---

1：结构体类型的声明与变量的定义

        结构：结构是一些值的集合，这些值指的是成员变量。结构体的成员变量可以是不同类型的变量。

        结构的声明-->

        

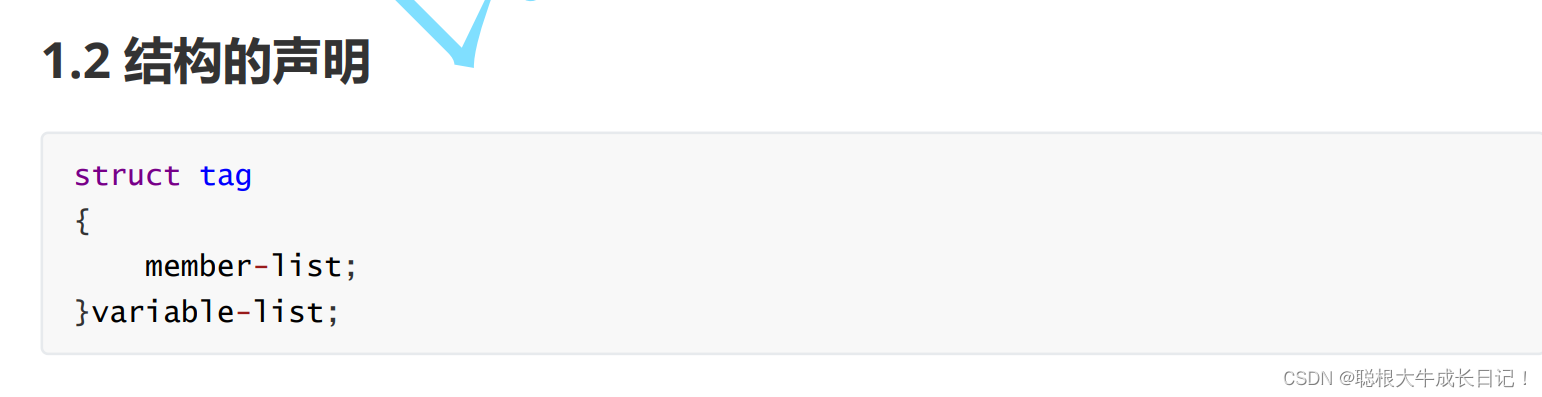
 tag:是可以自己起名字。

member_list:结构体的成员变量的类型声明。

variable_list:结构体变量可以在此定义。

如果将tag去掉的话，那么此结构体是一个特殊的声明也称结构体的不完全声明，定义变量的时候只能在variable-list此处定义。‘

struct tag才叫结构体的定义类型。

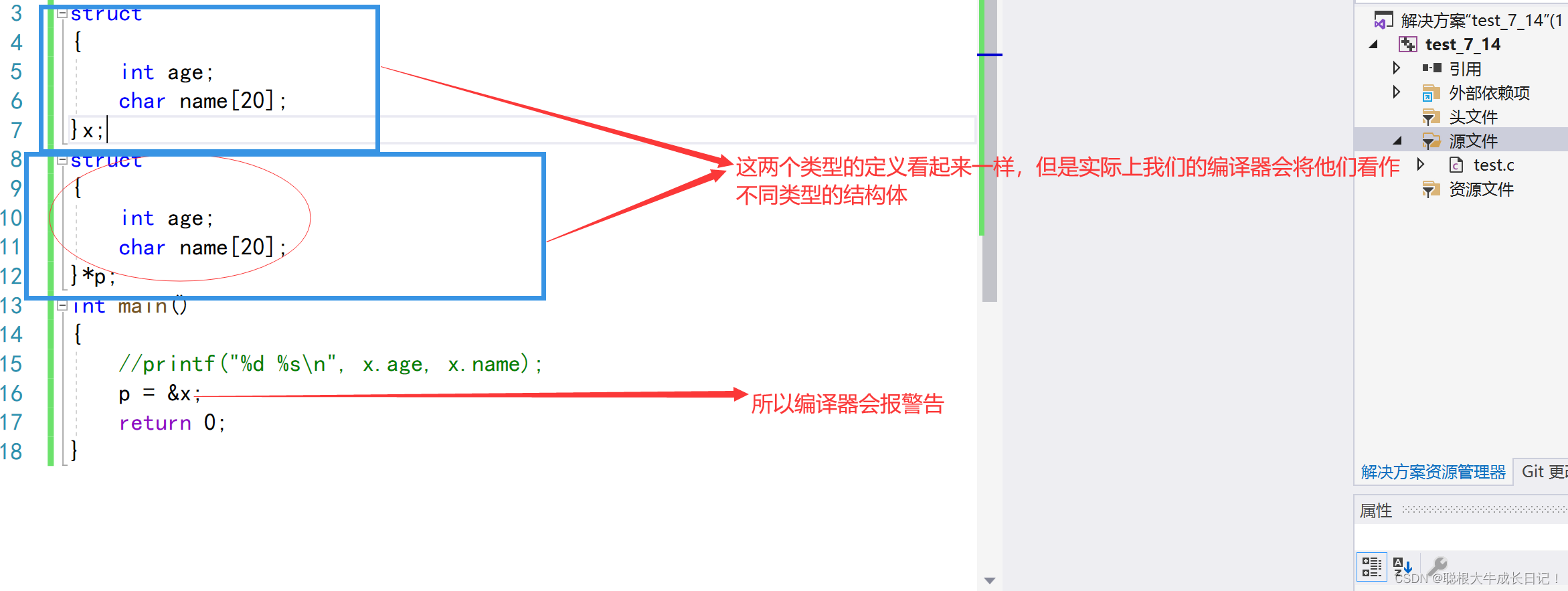
 如果定义两个匿名结构体类型的话，尽管他们的成员变量相同但是编译器会认为他们的类型是不同的。所以此时如果用结构体指针指向另外一个结构体是非法的 。

  结构体的自引用：即结构体里面包含指向自身结构的指针。

        不能是结构体的原因：假设是结构体里面包含结构体，则会形成无限套娃的形式sizeof(结构体)的大小就不能够计算出来了。

结构体变量的定义与初始化

结构体变量的定义可以分为两种情况下定义：

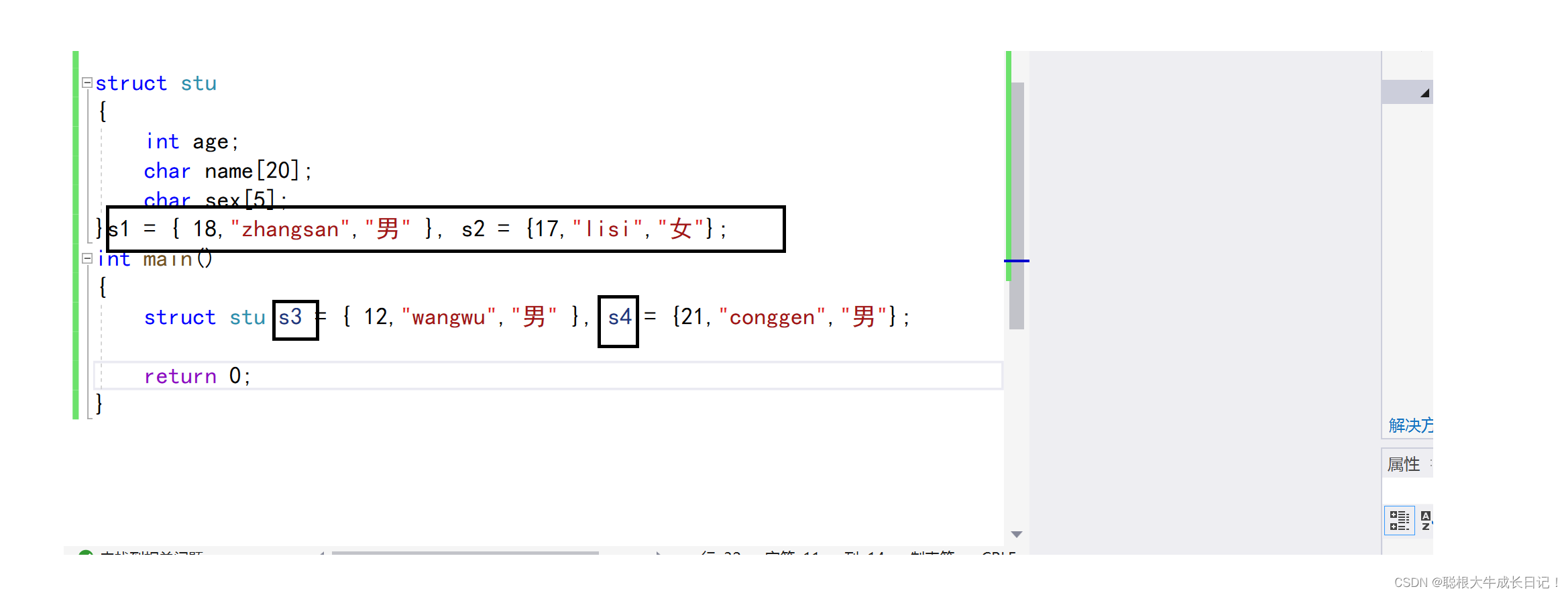                1：在结构体声明的时候定义变量与进行初始化.s1,s2

        2：在用类型加变量名定义的时候初始化。s3,s

      2:求解结构体的大小(结构体的内存对齐)

        首先我们来了解结构体的对齐规则：

                1：结构体的第一个成员在结构体偏移量为0的地址处，即结构体的起始位置开始处。

                2：其他成员变量对齐到某个对齐数的整数倍的地址处。

                        对齐数=结构体成员本身的大小与编译器默认的对齐数的较小值

                3：结构体的最终大小为最大对齐数(每个成员变量对齐数的最大值)的整数倍

                4:如果包含结构体嵌套，那么嵌套的结构体对齐到自身最大对齐数的整数倍地址处，结构体的整体大小就是所有最大对齐数(含嵌套结构体)的整数倍处。

           练习：

        

struct S1
{
 char c1;
 int i;
 char c2;
};

printf("%d\n", sizeof(struct S1));

     图解：

解释：首先我们先将c1变量放在偏移量为0的地址处，大小为1个字节。

        i的大小为4个字节而vs默认对齐数为8，所以对齐数为4，所以我们的结构体就会浪费3个字节的空间使i偏移到地址为4处开始

        c2变变量自身大小为1，对齐数为1所以c2变量直接在i后1个字节的空间就行。

        现在的大小为9个字节，根据第三条规则，结构体的大小为最大对齐数的整数倍，而此处大小为4，所以还要浪费三个字节的空间，所以最终答案为12. 

为啥会存在结构体内存对齐呢？

        平台原因：不是所有的硬件平台都够访问任意地址上的任意处的数据，如果访问的话则会抛出硬件异常。

        性能原因：数据结构(尤其是栈)，如果内存未对齐那么我们的处理器需要两次内存访问，而对齐了的话则只需要一次访问就行

    总的来说：结构体内存对齐就是拿空间来换时间。

为了即提高空间的效率与时间的效率，避免浪费太多的空间，我们可能会使成员变量小的尽可能放在一起  

我们可以使用 #pragma pack()   来改变平台默认对齐数

3：结构体传参与位段

结构体传参的时候可以传结构体，也可以传地址，那么我们应该选哪个呢？

        一般我们都会选择传地址，这是因为形式参数会在内存中进行压栈等操作，会浪费一定的时间与空间，如果结构体足够大，那么形式参数所需要的时间与空间的消耗更大，导致性能的下降。

        结论：结构体传参的时候传地址。

位段：

        其实位段也是在结构体的基础上进行的操作，只是说它的语法不完全相同如：

        

struct s
{
    int a:4;
    int b:5;
    int c:6;
    //位段的成员名后边有一个冒号和一个数字
    //位段成员的类型必须为整形家族的
    
};

        这些后面的数字单位都是字节

位段开辟空间的时候一般是按照4个字节的空间开辟或者是按照1个字节的空间开辟

当既有整形又有字符型的时候一般都是按照整形进行开辟空间的

4：枚举的定义与优点

        定义：涉及一个关键字enum，生活中有些事物是可以一一列举出来的，枚举就是将所有可能一一列举出来的，比如说一周有多少天，三原色，性别...

        

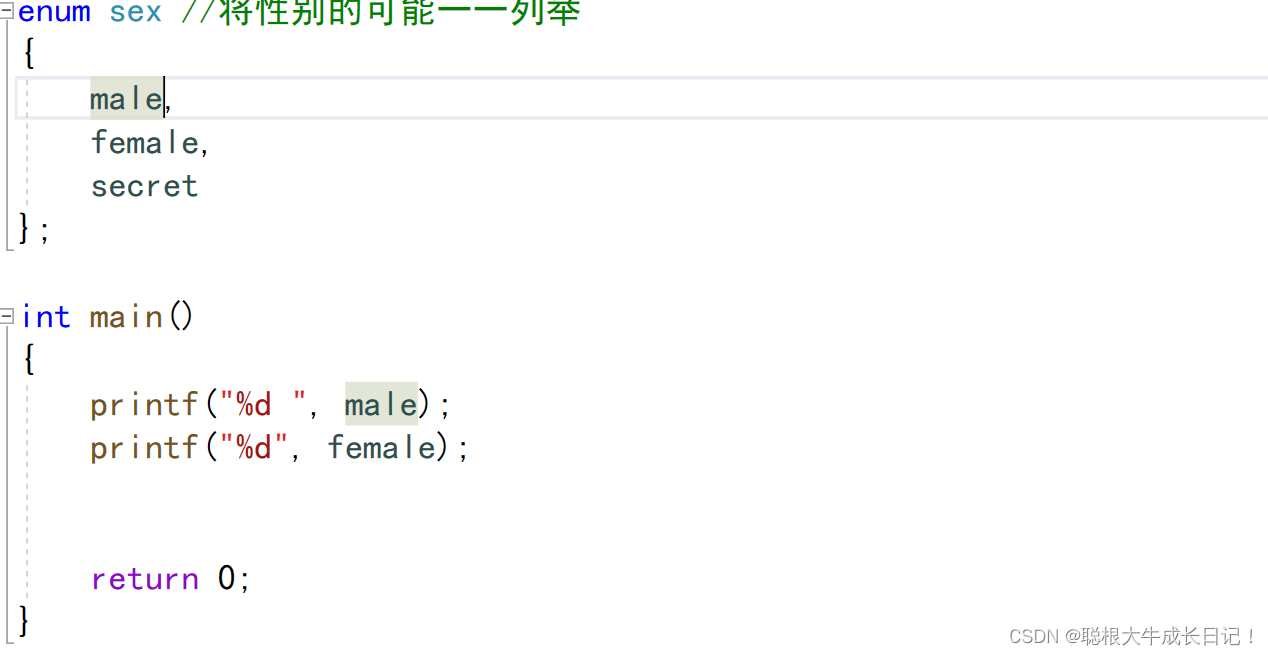
在enum{}当中的成员，又可以叫做枚举常量，且他们的值是依次递增1的，当然也可以给他们赋值。其中enum sex称作枚举类型

 优点：

        与#define相比，   1.枚举可以增加代码的可读性和可维护性

                                      2.与#define相比枚举定义的常量有类型检查，更加严谨

                                       3.便于调试

                                       4.使用方便1次可以定义多个常量

只能拿枚举常量给枚举变量赋值。其他类型的常量会error

5：共用体的定义与特点及大小的计算

共用体:一般用union来定义比如：

union Un

{
 char c;
 int i;
};

特点：是共用体共用同一块内存空间，也就是说共用体的大小最小为成员变量类型的最大值

共用体的计算：

联合的大小至少是最大成员的大小。

当最大成员大小不是最大对齐数的整数倍的时候，就要对齐到最大对齐数的整数倍。

                        感谢大家的观看！