文章目录
- 🔍 选择排序的原理与过程
- 📈 选择排序的优缺点
- 👉 代码实现
🔍 选择排序的原理与过程
本文我们直接说一个优化过的直接选择排序。其思路大同小异.
- 选择排序的思路很简单
每次从待排序的数据中选择一个最小和最大的元素,最小的存放在序列的起始位置,最大的元素放在序列的尾部,直到全部待排序的数据元素排完 。
- 在元素集合array[i]–array[n-1]中选择关键码最大和最小的数据元素.
- 找到最大值将其和数据序列末尾交换,找到最小值将其跟数据序列起始位置交换
- 在剩余的array[i+1]–array[n-2]集合中,重复上述步骤,直到集合剩余1个元素.
- 数据演示
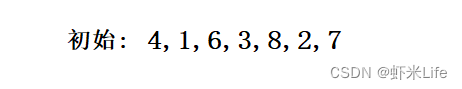
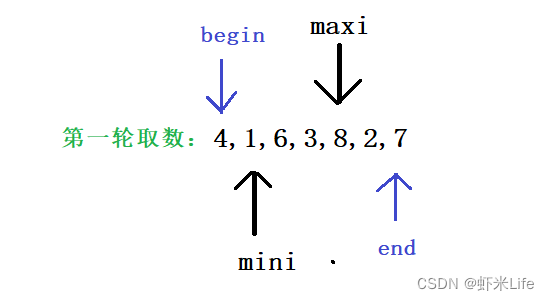
- 第一轮取数结果
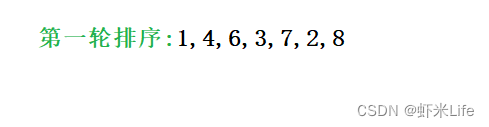
- 第二轮取数结果
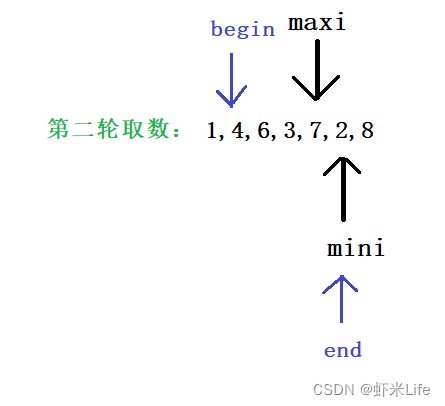
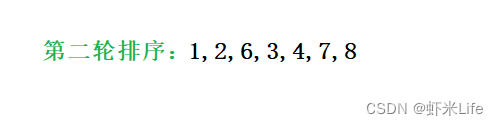
3. 第三轮取数结果


📈 选择排序的优缺点
直接选择排序的特性总结:
- 优点
- 实现简单:选择排序的实现非常简单,容易理解和实现,不需要复杂的数据结构或算法思想,适合初学者或快速解决一些小型排序问题。
- 空间复杂度低:选择排序只需要用到常数个变量作为辅助空间,不需要额外开辟内存空间来存储排序结果,因此空间复杂度较低.所有他的空间复杂度为O(1)
- 缺点:
- 时间复杂度高:选择排序的时间复杂度为O(n^2),其中n是数组长度,因此性能较差,不适合处理较大规模的数据。
- 不稳定:选择排序的交换过程可能会破坏数组中相同大小元素的稳定性,因此选择排序是一种不稳定的排序算法。
👉 代码实现
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1; // 定义排序区间的起点和终点
while (begin < end) // 当起点小于终点时,继续排序
{
int maxi = begin, mini = begin; // 定义当前区间最大值和最小值的下标
for (int i = begin; i <= end; i++) // 遍历当前区间
{
if (a[i] > a[maxi]) // 如果当前元素大于最大值,更新最大值下标
{
maxi = i;
}
if (a[i] < a[mini]) // 如果当前元素小于最小值,更新最小值下标
{
mini = i;
}
}
Swap(&a[begin], &a[mini]); // 将最小值和当前区间起点交换位置
// 如果最大值下标和起点下标重叠,修正一下最大值下标即可
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]); // 将最大值和当前区间终点交换位置
++begin; // 起点向右移动一位
--end; // 终点向左移动一位
}
}
代码实现起来比较简单:
但是要注意一个点如果最大值下标和起点下标重叠,需要做一下处理.
if (begin == maxi)
{
maxi = mini;
}
这行代码的意思是判断最大值下标是否和起点下标重叠,如果重叠则最大值已经被移动到了最小值下标处了,需要将最大值下标更新为最小值下标,否则下一步交换操作会将最大值和起点处的元素交换,而不是最大值和终点处的元素交换。举个例子
当待排序数组为 {5, 2, 3, 4, 1} ,第一轮排序时,最小值为1,最大值为5,
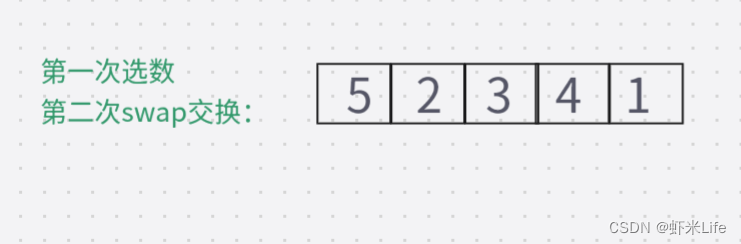
第一次swap交换后数组变为 {1, 2, 3, 4, 5},在第二次swap交换时如果没有判断:此时的最大值下标仍然指向起点位置,直接swap交换则数据会变成{5,2,3,4,1},导致排序错误。如加上判断:更新maxi的下标, maxi = mini;此时maxi的下标指向了4,再次swap数据.排序成功。因此,需要判断最大值下标和起点下标是否重叠,如若重叠,需要将最大值下标更新为最小值下标,即maxi=mini。
- 图析:
- 在没有判断条件下进行:
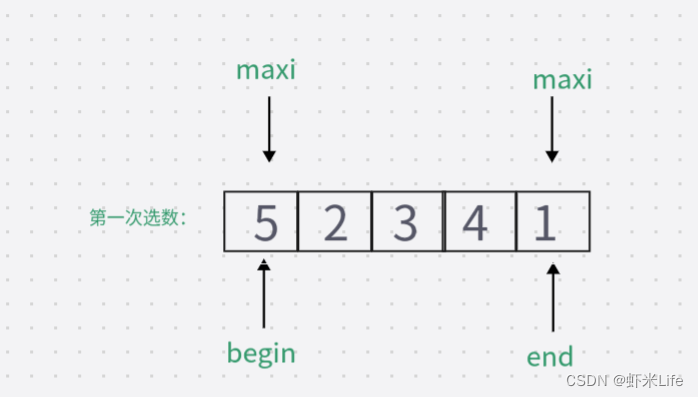
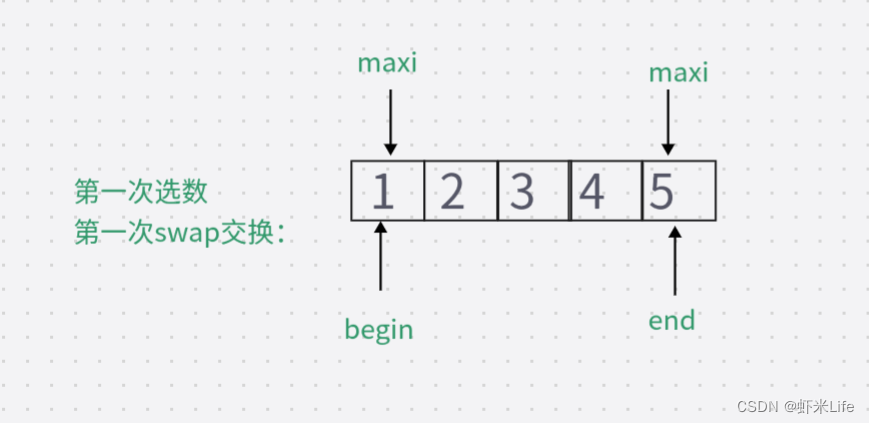
此时的maxi还依然指向begin起始位置,再次交换就会出错.
- 加上判断条件的进行
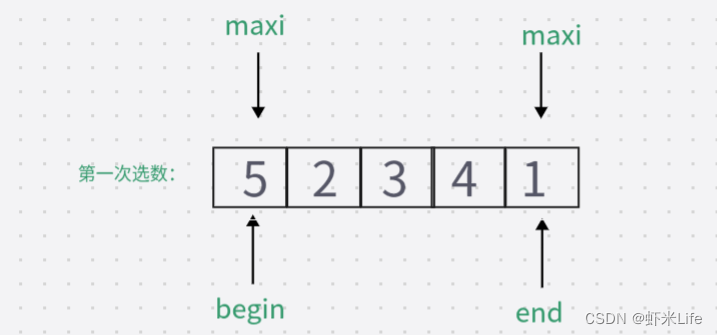
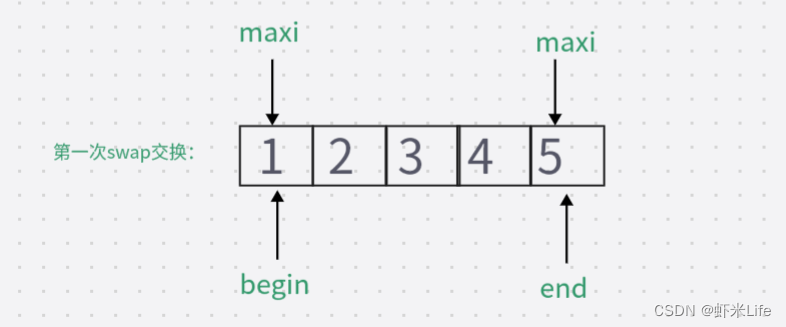
加上判断条件后if(begin == maxi)成立,则maxi = mini;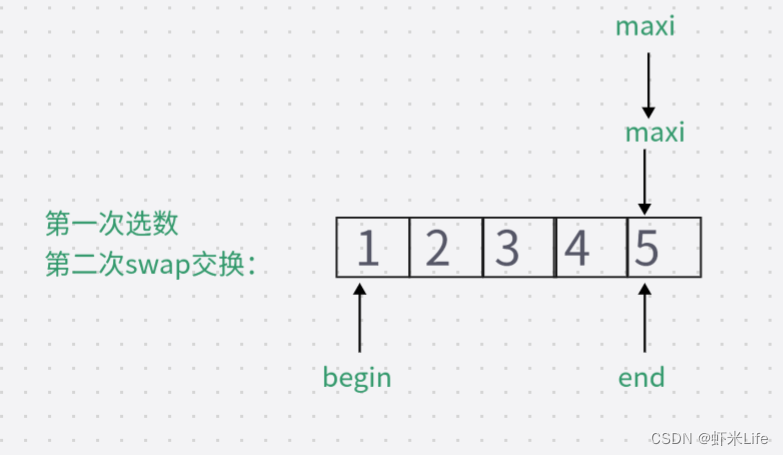
排序成功.
- 选择排序的优点是简单易懂,缺点是效率低,不适用于大规模数据的排序。在实际应用中,一般用来作为其他排序算法的子过程。但是该选择排序算法还是值得我们去学习摸索的,