兜兜转转,一晃年关将至。时间证明了一个道理,学啥忘啥,学的越快忘得越快,还不如踏踏实实写点笔记心得来的实在。
编程初学期间,排序算法是让人抓头最多的一块。为什么我连最简单的冒泡排序都理解不了,我是不是不选错专业了,很多人会有这样的疑问,然后就有人做gif冒泡懵逼排序,别说,还挺形象的。
其实排序算法这块,着急不得,这个排序算法不会就换一个排序算法来学,总有一种排序算法你能够理解的,等需要用到排序的时候,你只要会一种就可以了。
在这里我列举了7中常见的排序算法并用C语言实现,你们可能就要问了,不是十种吗?怎么还能缺斤短两,不是我不会写啊,是写起来麻烦,你们也用不到后面那几种,跟别说去研究了,能看懂常见的七种排序算法你就能在学校里横着走了。
后台回复【排序算法】可以拿到全部代码
目录
一、冒泡排序
二、选择排序
三、插入排序
四、快速排序
五、希尔排序
六、归并排序
七、桶(基数)排序
01
冒泡排序
相信大家最熟悉的就是冒泡排序了,这个我就不多说
直接上动图演示原理,外加代码实现冒泡排序:

C语言代码实现:
void BubbleSort(int arr[], int n){//从小到大排序 相邻来两个数比较,将大的数字往后放for (int i = 0; i < n - 1; i++) //n-1是因为数组下标最大为n-1 要进行10轮比较{//n-1是因为数组下标最大为n-1 要进行10次比较,再减i是因为每最后的i个元素已经有序不需要继续排序for (int j = 0; j < n - 1 - i; j++){if (arr[j] > arr[j + 1]) //两两比较,将小的数据放前面{swap(arr, j + 1, j); //交换arr数组arr[j+1]和arr[j]的值}}}}//交换函数后面就不列举了,凡是swap都是下面代码实现的void swap(int arr[], int x, int y){int temp = arr[x];arr[x] = arr[y];arr[y] = temp;}
02
选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾,重复操作。
动图演示原理,外加代码实现选择排序:

C语言代码实现:
void SelectSort(int arr[], int n){for (int i = 0; i < n - 1; i++){for (int j = i + 1; j < n; j++){if (arr[i] > arr[j]){swap(arr, i, j); //交换arr数组arr[i]和arr[j]的值}}}}
03
插入排序
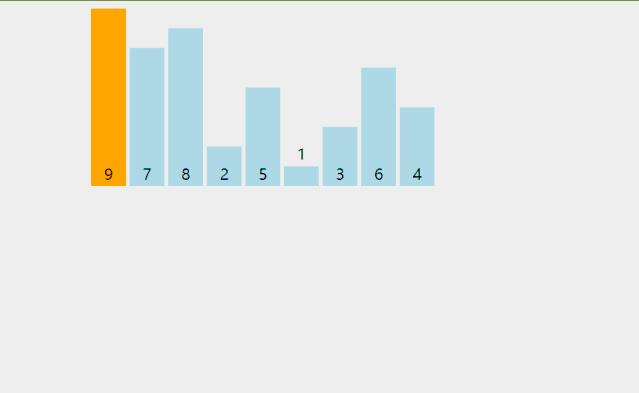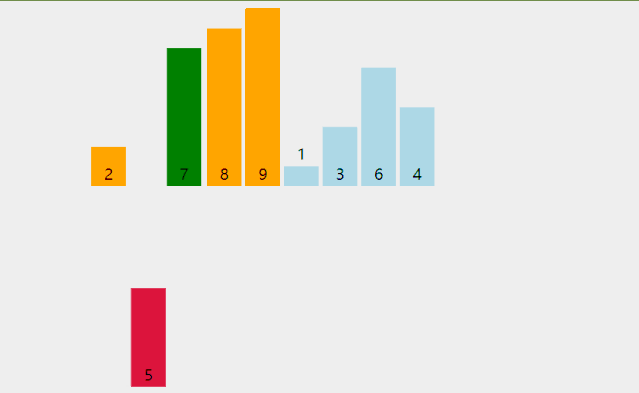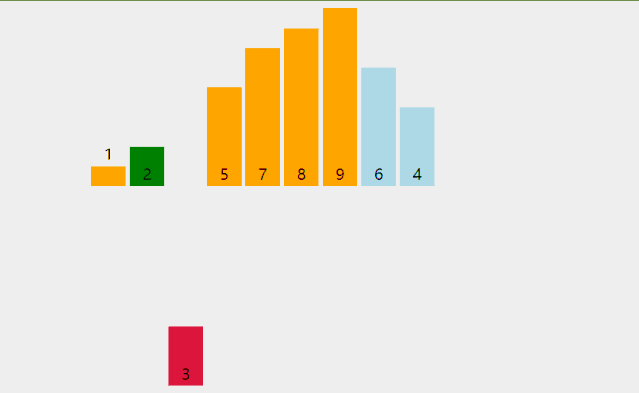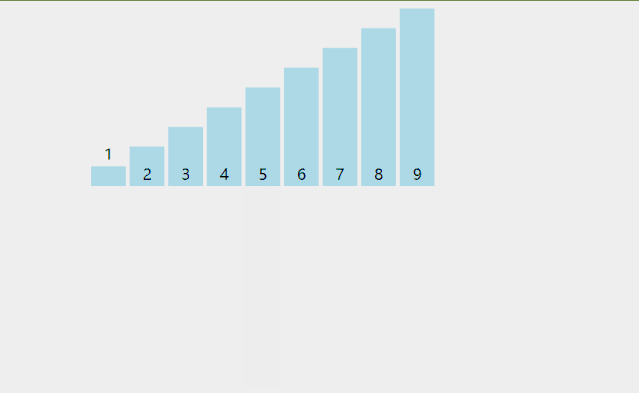
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的,就是将未排序的数字插入到已排序的数列中。
动图演示原理,外加代码实现插入排序:
C语言代码实现:
void InsertSort(int arr[], int n){int tempVal;for (int i = 1, j; i < n; i++){tempVal = arr[i]; //保存要插入的值for (j = i - 1; tempVal < arr[j] && j >= 0; --j) //数据往后移动,给要插入的值腾位{arr[j + 1] = arr[j];}arr[j + 1] = tempVal; //插入数据}}
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。插入排序是将未排序的数字插入到已排序数列中,而希尔排序是将一个已排序的数列插入到另一个已排序的数列中。
示意图演示原理,外加代码实现希尔排序:

C语言代码实现:
void ShellSort(int arr[], int n){int tempVal, j;int jump = n >> 2; //步长值while (jump != 0){for (int i = jump; i < n; i++){tempVal = arr[i]; //保存待排序的第一个数,也就是待插入的数for (j = i - jump; j >= 0 && tempVal < arr[j]; j -= jump){arr[j + jump] = arr[j];}arr[j + jump] = tempVal;}jump = jump >> 1; //步长值减半}}
06
归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。
示意图演示原理,外加代码实现归并排序:

C语言代码实现:
void MergeSort(int arr[], int left, int right){if (left >= right)//递归的终止条件,left == right证明这个区间只有一个元素,不需要再拆了return;int mid = ((right - left) >> 1) + left;//求中点MergeSort(arr, left, mid); //拆分左MergeSort(arr, mid + 1, right); //拆分右//并操作_merge_in_arr(arr, left, mid, right);}void _merge_in_arr(int arr[], int left, int mid, int right){int length = right - left + 1; //定义一个辅助的空间的长度int *pData = (int*)malloc(sizeof(int)*length);//分配一个动态内存来调整元素的位置memset(pData, 0, sizeof(int)* length);//合并int low = left; //左边区间的起始下标int hig = mid + 1; //右边区间的起始下标int index = 0; //辅助数组的下标while (hig <= right)//右区间没有合并完{while (low <= mid && arr[low] <= arr[hig])//证明左区间没有合并完,且左区间的值小于右区间的值{pData[index] = arr[low]; //把左边的值放进辅助数组low++; //左边往高位移,下一次需要判断左边的新下标index++; //下一次放进辅助数组的新下标}if (low > mid) //证明左区间已经放完break;while (hig <= right && arr[low] > arr[hig])//证明右区间没有合并完,且左区间的值大于右区间的值{pData[index] = arr[hig]; //把右边的值放进辅助数组hig++; //右边往高位移,下一次需要判断右边的新下标index++; //下一次放进辅助数组的新下标}}//到这一步,证明起码有一个区间已经合并完成if (hig <= right) //证明右边没有完成memmove(&pData[index], &arr[hig], sizeof(int)* (right - hig + 1));if (low <= mid) //证明左边没有完成memmove(&pData[index], &arr[low], sizeof(int)* (mid - low + 1));//把所有区间都合并到了辅助区间memmove(&arr[left], pData, sizeof(int)* length);free(pData); //释放空间}
07
桶排序
桶排序是典型的空间换时间,在对整数排序中,没有什么算法能比它还快,但是在空间浪费上,它是祖宗。
示意图演示原理,外加代码实现桶排序:

C语言代码实现:
void radix_sort(int arr[], size_t len){int**temp = (int **)malloc(sizeof(int) * 10); //10行//申请动态内存 辅助数组temp[10][];for (int i = 0; i < 10; i++){temp[i] = (int *)malloc(sizeof(int)*len);}for (int i = 1; i <= 100; i *= 10)//循环数值可能有的位数{for (int x = 0; x < 10; ++x)//辅助数组行循环{for (int y = 0; y < len; ++y)//辅助数组列循环{temp[x][y] = -1;//辅助数组的初始化赋值,-1表示在arr里面不可能出现的数值}}//arr数组中的元素放入辅助数组for (int m = 0; m < len; ++m){int index = (arr[m] / i) % 10;temp[index][m] = arr[m];}//把辅助数组的内容放回待排序数组int k = 0;//待排序的下标for (int x = 0; x < 10; x++){for (int y = 0; y < len; ++y){if (temp[x][y] != -1)arr[k++] = temp[x][y];}}}//释放内存for (int i = 0; i < 10; i++){free(temp[i]);}free(temp);}
续
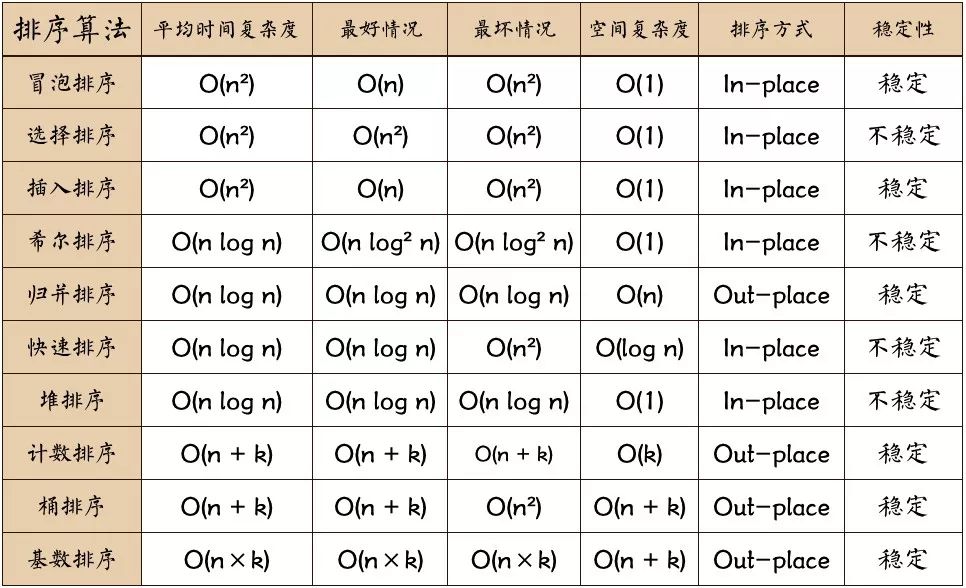
算法复杂度
这个算法的复杂度纯理论,我就放到最后来讲
一个时间复杂度,一个空间复杂度
一个稳定,一个不稳定
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
附录:






![已解决 BrokenPipeError: [Errno 32] Broken pipe](https://img-blog.csdnimg.cn/5c362be60c6c42fbb7bec33aa09ecb1e.png)