题目

给定一个n个点m条边的无向图，图中可能存在重边和自环。
请你判断这个图是否是二分图。

输入格式

第一行包含两个整数n和m。
接下来m行，每行包含两个整数u和v，表示点u和点v之间存在一条边。

输出格式

如果给定图是二分图，则输出"Yes"，否则输出No”。

数据范围

1 ≤n, m ≤ 10⁵

• 输入样例:

4 4
1 3
1 4
2 3
2 4

• 输出样例:

Yes

题解

import java.util.Arrays;
import java.util.Scanner;

/**
 * @author akuya
 * @create 2023-07-11-20:31
 */
public class dye {
    static int N=100010;
    static int M=200010;
    static int n,m;
    static int h[]=new int [N];
    static int e[]=new int[N];
    static int ne[]=new int [M];
    static int idx;
    static int color[]=new int[N];
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        m=scanner.nextInt();
        Arrays.fill(h,-1);

        while(m--!=0){
            int a ,b;
            a=scanner.nextInt();
            b=scanner.nextInt();
            add(a,b);
            add(b,a);
        }

        boolean flag=true;
        for(int i=1;i<=n;i++){
            if(color[i]==0){
                if(!dfs(i,1)){
                    flag=false;
                    break;
                }
            }
        }

        if(flag) System.out.println("Yes");
        else System.out.println("No");

    }
    public static void add(int a,int b){
        e[idx]=b;ne[idx]=h[a];h[a]=idx++;
    }
    public static boolean dfs(int u,int c){
        color[u]=c;
        for(int i=h[u];i!=-1;i=ne[i]){
            int j=e[i];
            if(color[j]==0){
                if(!dfs(j,3-c))return false;
            }
            else if(color[j]==c) return false;
        }

        return true;
    }


}

思路

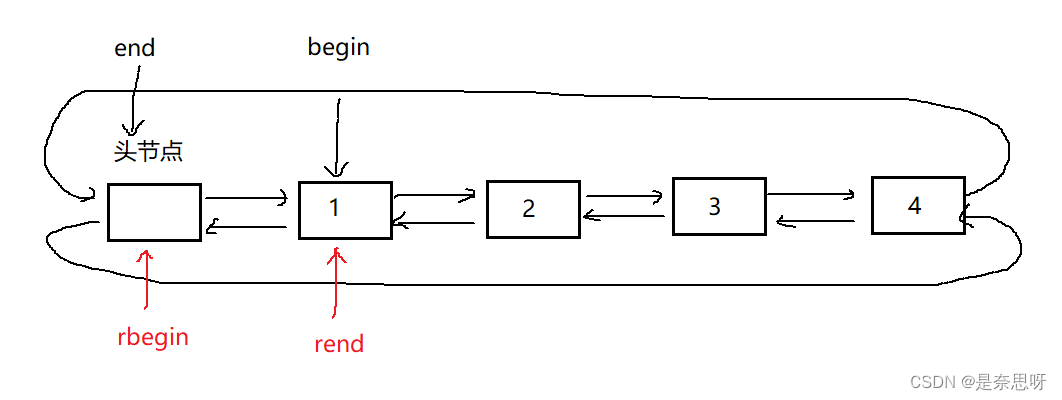
由图所示，如果是二分图，不会含有奇数环，因此我们深搜遍历，1节点的子节点为2，2节点的子节点为1，不满足则不是二分图。