💖作者:小树苗渴望变成参天大树🎈
🎉作者宣言:认真写好每一篇博客💤
🎊作者gitee:gitee✨
💞作者专栏:C语言,数据结构初阶,Linux,C++ 动态规划算法🎄
如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧!
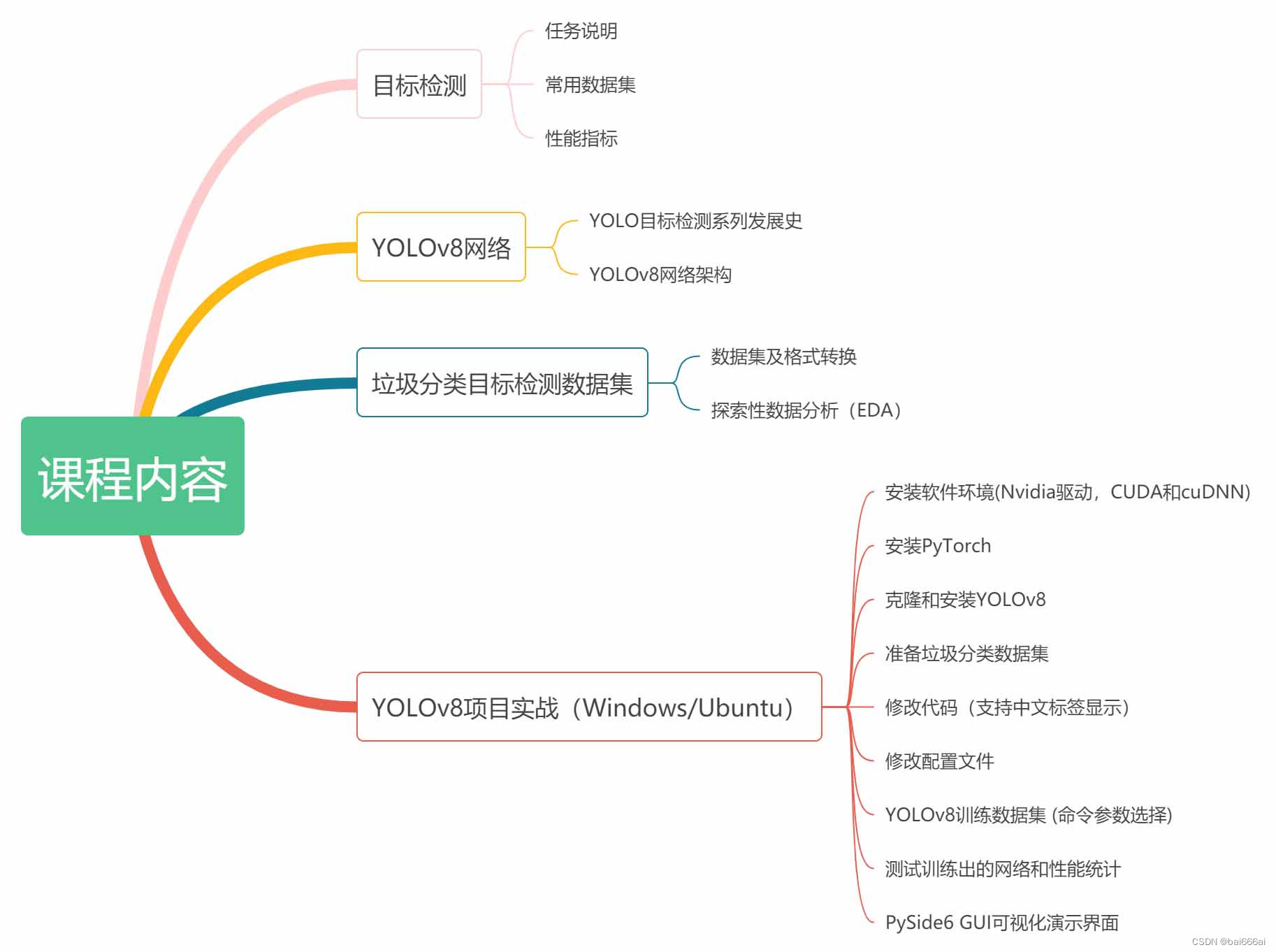
文章目录
- 前言
- 一、[杨辉三角](https://leetcode.cn/problems/pascals-triangle/)
- 二、[电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)
前言
🎆上一期我们专门学习了vector是怎么使用的,今天我们来做两个题目,来将vector放到题目当中进行运用,这两个题目会涉及到二维数组,我会通过画图来给大家进行讲解,话不多说,我们进入正文
一、杨辉三角
✨对于杨辉三角的题目,大家在C语言阶段也做过,下面的动图很好的解释了杨辉三角的原理
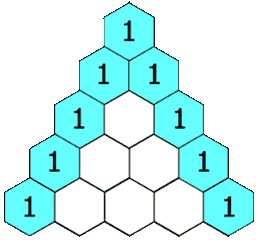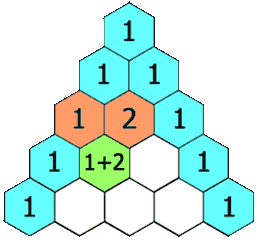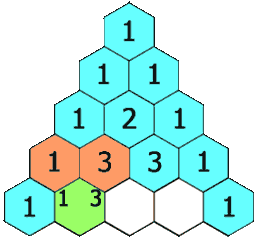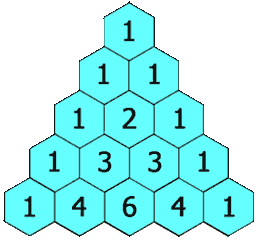
这个动图不方便后面的讲解,我在画一个图:
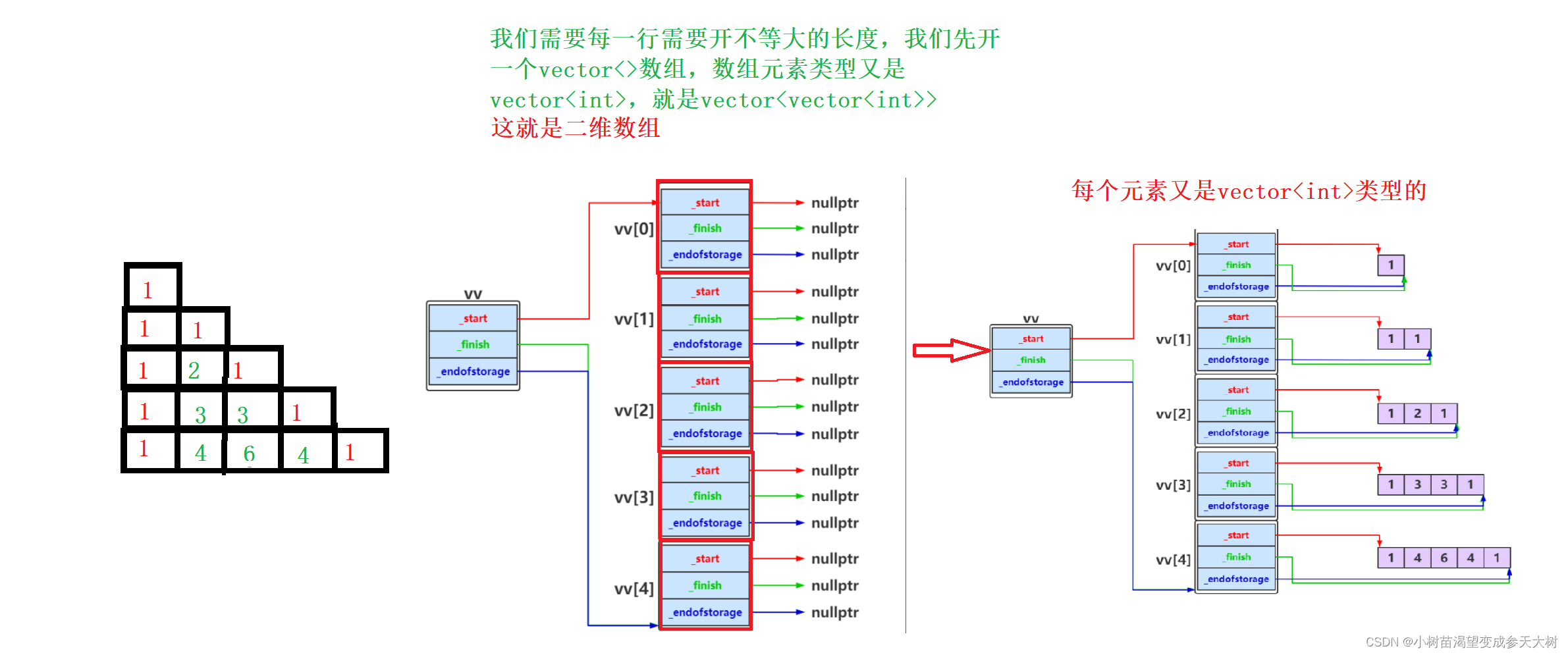
对于这个题目就是先把第一列和对角线初始化为0,其余的在按照规则填写数字,我们来看代码实现:
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> v;
v.resize(numRows);//先把多少行开好
for(int i=0;i<numRows;i++)
{
v[i].resize(i+1,0);//每行开多大
v[i][0]=1;//第一列初始化为1
v[i][i]=1;//对角线初始化为1
}
for(int i=1;i<v.size();i++)
{
for(int j=1;j<v[i].size();j++)
{
if(v[i][j]==0)//为0的地方都是没有填的
v[i][j]=v[i-1][j-1]+v[i-1][j];//左上角和上面元素的和
}
}
return v;
}
};
我们直接返回这个二维数组就可以,对于我们的C语言使用二维数组解题,就方便很多,通过传的参数,我们就感觉头大,它要返回二级指针,多少行每行多少个都要记录下来。vector就很好的解决这个问题,让你不想碰C语言
二、电话号码的字母组合
🎈

来看图解:
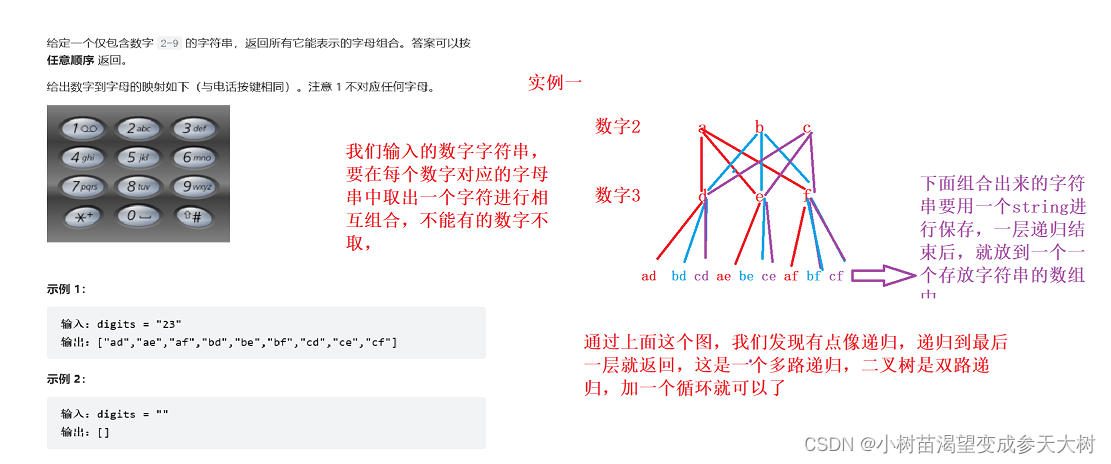
我们来看代码实现:
class Solution {
string strA[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};//使用下标将数字匹配的字母先存放起来,下标就对应相应的数字
public:
vector<string> letterCombinations(string digits) {
vector<string> v;
if(digits.empty())//特殊情况
return v;
combineStr(digits,0,"",v);//从第0层开始匹配,一开始的字符串是空串
return v;
}
void combineStr(string digits,int level,string combinestr,vector<string>& v)
{//第一个参数是传进来的数字字符串
//第二个参数是递归到多少层,有几个数字就有几层
//第三个参数是存放单词匹配好的字符串,这里不能用引用,因为不能改变改变当前层的字母组合
//第四个参数是存放匹配好的字符串的数组,因为要每次匹配好都要进行存放,所以传引用
if(level==digits.size())//递归到最后一层的下一层开始返回
{
v.push_back(combinestr);
return;
}
int nums=digits[level]-'0';//取出对应的数字
string str=strA[nums];//数字对应的字符串
for(int i=0;i<str.size();i++)//多路递归,之前的二叉树都是双路递归
{
combineStr(digits,level+1,combinestr+str[i],v);
}
}
};
递归展开图:
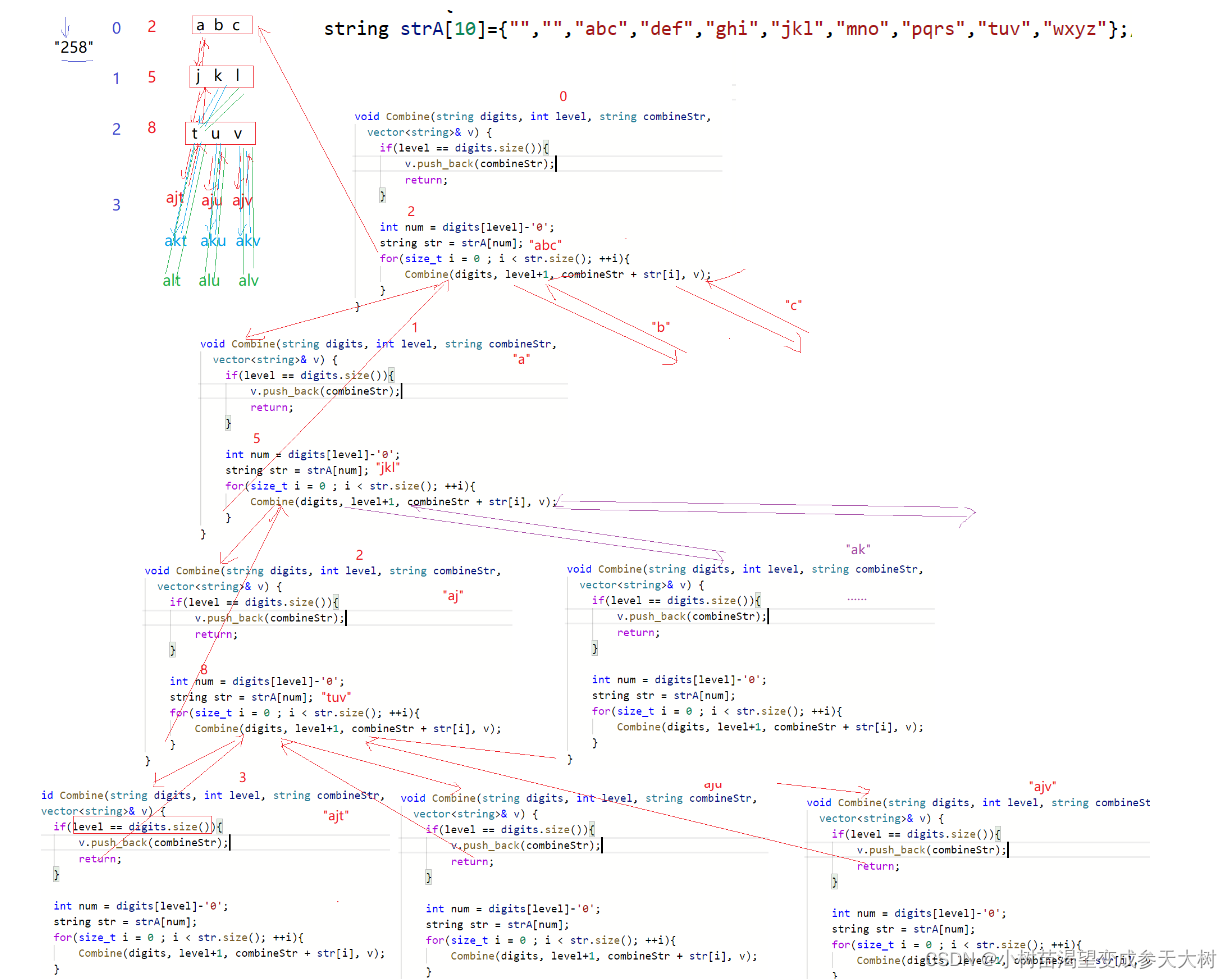
递归展开图只画了一次匹配,太多了画不下去,其余的都是一样的道理,这个题目难度还有的,大家下去好好理解一下
今天的两道题就讲解到这里了,讲解这个两个题目就是为了让大家认识到用vector怎么表示二维数组,并且知道vector是多么方便,如果大家不信,可以使用C语言进行写着两道题目看看,相信大家肯定会很难受,下一篇我就带大家模拟实现一下vector,看看vector的底层是怎么实现的吧,我们下篇再见





![已解决 BrokenPipeError: [Errno 32] Broken pipe](https://img-blog.csdnimg.cn/5c362be60c6c42fbb7bec33aa09ecb1e.png)