目录
1 灰狼优化算法基本思想
2 灰狼捕食猎物过程
2.1 社会等级分层
2.2 包围猎物
2.3 狩猎
2.4 攻击猎物
2.5 寻找猎物
3 实现步骤及程序框图
3.1 步骤
3.2 程序框图
4 Python代码实现
5 Matlab实现
1 灰狼优化算法基本思想
灰狼优化算法是一种群智能优化算法,它的独特之处在于一小部分拥有绝对话语权的灰狼带领一群灰狼向猎物前进。在了解灰狼优化算法的特点之前,我们有必要了解灰狼群中的等级制度。


灰狼群一般分为4个等级:处于第一等级的灰狼用α表示,处于第二阶级的灰狼用β表示,处于第三阶段的灰狼用δ表示,处于第四等级的灰狼用ω表示。按照上述等级的划分,灰狼α对灰狼β、δ和ω有绝对的支配权;灰狼ω对灰狼δ和ω有绝对的支配权;灰狼δ对灰狼ω有绝对的支配权。
2 灰狼捕食猎物过程
GWO 优化过程包含了灰狼的社会等级分层、跟踪、包围和攻击猎物等步骤,其步骤具体情况如下所示。
2.1 社会等级分层
当设计 GWO 时,首先需构建灰狼社会等级层次模型。计算种群每个个体的适应度,将狼群中适应度最好的三匹灰狼依次标记为


编辑、


、


而剩下的灰狼标记为


。也就是说,灰狼群体中的社会等级从高往低排列依次为
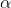

编辑、


、


及


。GWO 的优化过程主要由每代种群中的最好三个解(即
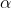

、


、


)来指导完成。
2.2 包围猎物
灰狼群体通过以下几个公式逐渐接近并包围猎物:


式中,t是当前的迭代代数,A和C是系数向量,Xp和X分别是猎物的位置向量和灰狼的位置向量。A和C的计算公式如下:
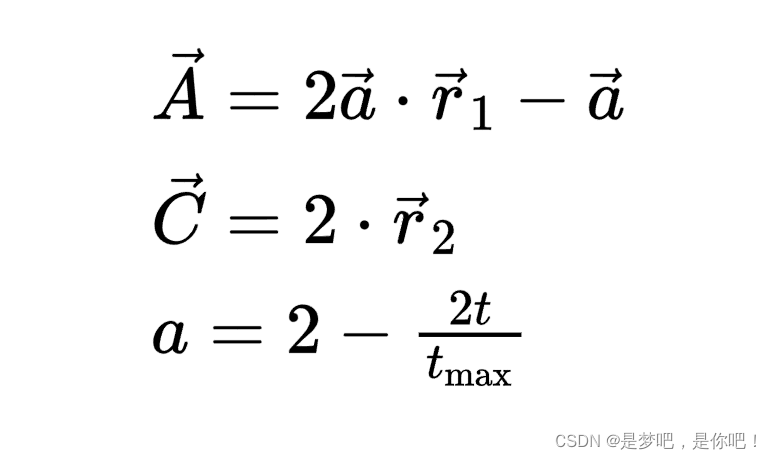

式中,a是收敛因子,随着迭代次数从2线性减小到0,r1和r 2服从[ 0,1]之间的均匀分布。
2.3 狩猎
狼群中其他灰狼个体Xi根据α、β和百的位置Xa、XB和Xo来更新各自的位置:

式中,Da,Dβ和D6分别表示a,β和5与其他个体间的距离;Xa,Xβ和X6分别代表a,β和5的当前位置;C1,C2,C3是随机向量,X是当前灰狼的位置。
灰狼个体的位置更新公式如下:
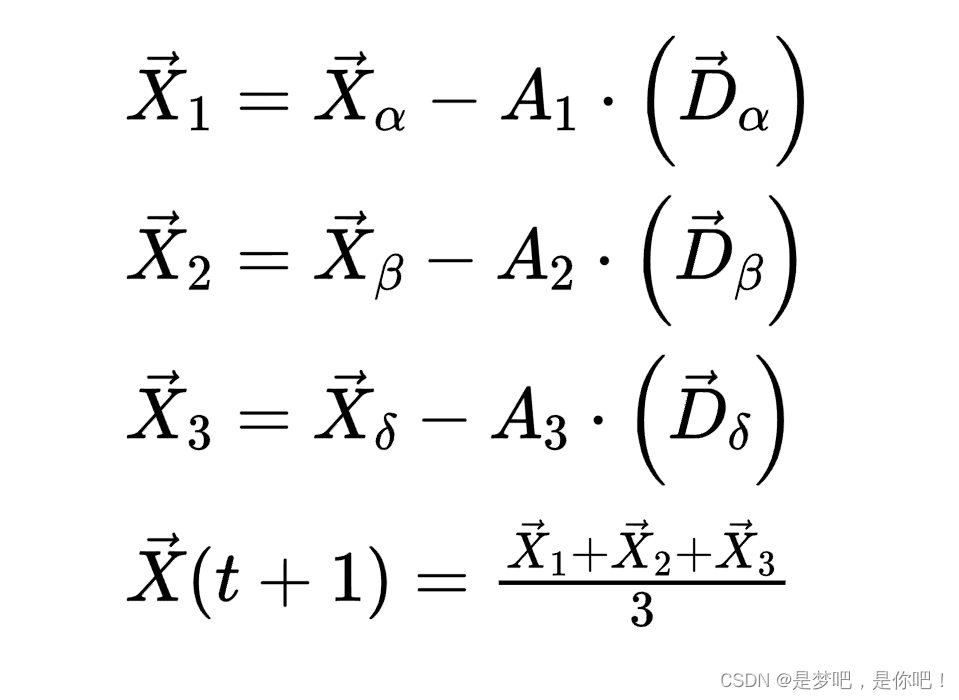

2.4 攻击猎物
构建攻击猎物模型的过程中,根据2)中的公式,a值的减少会引起 A 的值也随之波动。换句话说,A 是一个在区间[-a,a](备注:原作者的第一篇论文里这里是[-2a,2a],后面论文里纠正为[-a,a])上的随机向量,其中a在迭代过程中呈线性下降。当 A 在[-1,1]区间上时,则捜索代理(Search Agent)的下一时刻位置可以在当前灰狼与猎物之间的任何位置上。
2.5 寻找猎物
灰狼主要依赖


、


、
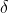

的信息来寻找猎物。它们开始分散地去搜索猎物位置信息,然后集中起来攻击猎物。对于分散模型的建立,通过|A|>1使其捜索代理远离猎物,这种搜索方式使 GWO 能进行全局搜索。GWO 算法中的另一个搜索系数是C。从2.2中的公式可知,C向量是在区间范围[0,2]上的随机值构成的向量,此系数为猎物提供了随机权重,以便増加(|C|>1)或减少(|C|<1)。这有助于 GWO 在优化过程中展示出随机搜索行为,以避免算法陷入局部最优。值得注意的是,C并不是线性下降的,C在迭代过程中是随机值,该系数有利于算法跳出局部,特别是算法在迭代的后期显得尤为重要。
3 实现步骤及程序框图
3.1 步骤
Step1:种群初始化:包括种群数量N,最大迭代次数Maxlter,调控参数a,A,C.Step2:根据变量的上下界来随机初始化灰狼个体的位置X。
Step3:计算每一头狼的适应度值,并将种群中适应度值最优的狼的位置信息保存
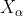

,将种群中适应度值次优的狼的位置信息保存为


,将种群中适应度第三优的灰狼的位置信息保存为


。
Step4:更新灰狼个体X的位置。
step5:更新参数a,A和C。
Step6:计算每一头灰狼的适应度值,并更新三匹头狼的最优位置。
Step7:判断是否到达最大迭代次数Maxlter,若满足则算法停止并返回Xa的值作为最终得到的最优解,否则转到Step4。
3.2 程序框图
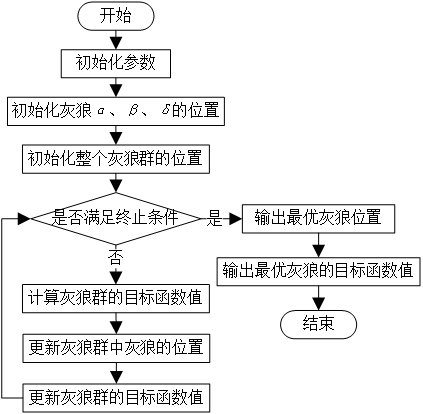

4 Python代码实现
#=======导入线管库======
import random
import numpy
def GWO(objf, lb, ub, dim, SearchAgents_no, Max_iter):
#===初始化 alpha, beta, and delta_pos=======
Alpha_pos = numpy.zeros(dim) # 位置.形成30的列表
Alpha_score = float("inf") # 这个是表示“正负无穷”,所有数都比 +inf 小;正无穷:float("inf"); 负无穷:float("-inf")
Beta_pos = numpy.zeros(dim)
Beta_score = float("inf")
Delta_pos = numpy.zeros(dim)
Delta_score = float("inf") # float() 函数用于将整数和字符串转换成浮点数。
#====list列表类型=============
if not isinstance(lb, list): # 作用:来判断一个对象是否是一个已知的类型。 其第一个参数(object)为对象,第二个参数(type)为类型名,若对象的类型与参数二的类型相同则返回True
lb = [lb] * dim # 生成[100,100,.....100]30个
if not isinstance(ub, list):
ub = [ub] * dim
#========初始化所有狼的位置===================
Positions = numpy.zeros((SearchAgents_no, dim))
for i in range(dim): # 形成5*30个数[-100,100)以内
Positions[:, i] = numpy.random.uniform(0, 1, SearchAgents_no) * (ub[i] - lb[i]) + lb[
i] # 形成[5个0-1的数]*100-(-100)-100
Convergence_curve = numpy.zeros(Max_iter)
#========迭代寻优=====================
for l in range(0, Max_iter): # 迭代1000
for i in range(0, SearchAgents_no): # 5
#====返回超出搜索空间边界的搜索代理====
for j in range(dim): # 30
Positions[i, j] = numpy.clip(Positions[i, j], lb[j], ub[
j]) # clip这个函数将将数组中的元素限制在a_min(-100), a_max(100)之间,大于a_max的就使得它等于 a_max,小于a_min,的就使得它等于a_min。
#===========以上的循环里,Alpha、Beta、Delta===========
a = 2 - l * ((2) / Max_iter); # a从2线性减少到0
for i in range(0, SearchAgents_no):
for j in range(0, dim):
r1 = random.random() # r1 is a random number in [0,1]主要生成一个0-1的随机浮点数。
r2 = random.random() # r2 is a random number in [0,1]
A1 = 2 * a * r1 - a; # Equation (3.3)
C1 = 2 * r2; # Equation (3.4)
# D_alpha表示候选狼与Alpha狼的距离
D_alpha = abs(C1 * Alpha_pos[j] - Positions[
i, j]); # abs() 函数返回数字的绝对值。Alpha_pos[j]表示Alpha位置,Positions[i,j])候选灰狼所在位置
X1 = Alpha_pos[j] - A1 * D_alpha; # X1表示根据alpha得出的下一代灰狼位置向量
r1 = random.random()
r2 = random.random()
A2 = 2 * a * r1 - a; #
C2 = 2 * r2;
D_beta = abs(C2 * Beta_pos[j] - Positions[i, j]);
X2 = Beta_pos[j] - A2 * D_beta;
r1 = random.random()
r2 = random.random()
A3 = 2 * a * r1 - a;
C3 = 2 * r2;
D_delta = abs(C3 * Delta_pos[j] - Positions[i, j]);
X3 = Delta_pos[j] - A3 * D_delta;
Positions[i, j] = (X1 + X2 + X3) / 3 # 候选狼的位置更新为根据Alpha、Beta、Delta得出的下一代灰狼地址。
Convergence_curve[l] = Alpha_score;
if (l % 1 == 0):
print(['迭代次数为' + str(l) + ' 的迭代结果' + str(Alpha_score)]); # 每一次的迭代结果
#========函数==========
def F1(x):
s=numpy.sum(x**2);
return s
#===========主程序================
func_details = ['F1', -100, 100, 30]
function_name = func_details[0]
Max_iter = 1000#迭代次数
lb = -100#下界
ub = 100#上届
dim = 30#狼的寻值范围
SearchAgents_no = 5#寻值的狼的数量
x = GWO(F1, lb, ub, dim, SearchAgents_no, Max_iter)



5 Matlab实现
% 主程序 GWO
clear
close all
clc
%输入关键字:灰狼算法
SearchAgents_no = 30 ; % 种群规模
dim = 10 ; % 粒子维度
Max_iter = 1000 ; % 迭代次数
ub = 5 ;
lb = -5 ;
%% 初始化三匹头狼的位置
Alpha_pos=zeros(1,dim);
Alpha_score=inf;
Beta_pos=zeros(1,dim);
Beta_score=inf;
Delta_pos=zeros(1,dim);
Delta_score=inf;
Convergence_curve = zeros(Max_iter,1);
%% 开始循环
for l=1:Max_iter
for i=1:size(Positions,1)
%% 返回超出搜索空间边界的搜索代理
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
%% 计算每个搜索代理的目标函数
fitness=sum(Positions(i,:).^2);
%% 更新 Alpha, Beta, and Delta
if fitness<Alpha_score
Alpha_score=fitness; % Update alpha
Alpha_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness<Beta_score
Beta_score=fitness; % Update beta
Beta_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score
Delta_score=fitness; % Update delta
Delta_pos=Positions(i,:);
end
end
a=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0
%% 更新搜索代理的位置,包括omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % Equation (3.3)
C1=2*r2; % Equation (3.4)
D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
r1=rand();
r2=rand();
A2=2*a*r1-a; % Equation (3.3)
C2=2*r2; % Equation (3.4)
D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2
r1=rand();
r2=rand();
A3=2*a*r1-a; % Equation (3.3)
C3=2*r2; % Equation (3.4)
D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3
Positions(i,j)=(X1+X2+X3)/3;% Equation (3.7)
end
end
Convergence_curve(l)=Alpha_score;
disp(['Iteration = ' num2str(l) ', Evaluations = ' num2str(Alpha_score)]);
end
%========可视化==============
figure('unit','normalize','Position',[0.3,0.35,0.4,0.35],'color',[1 1 1],'toolbar','none')
%% 目标空间
subplot(1,2,1);
x = -5:0.1:5;y=x;
L=length(x);
f=zeros(L,L);
for i=1:L
for j=1:L
f(i,j) = x(i)^2+y(j)^2;
end
end
surfc(x,y,f,'LineStyle','none');
xlabel('x_1');
ylabel('x_2');
zlabel('F')
title('Objective space')
%% 狼群算法
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r','linewidth',1.5)
title('Convergence_curve')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('GWO')
display(['The best solution obtained by GWO is : ', num2str(Alpha_pos)]);
display(['The best optimal value of the objective funciton found by GWO is : ', num2str(Alpha_score)]);