数据结构–树的存储结构
树的逻辑结构
树是
n
(
n
≥
0
)
n (n\ge0)
n(n≥0)个结点的有限集合,n = 0 时,称为空树,这是一种特殊情况。
在任意一棵非空树中应满足:
1)有且仅有一个特定的称为
根
\color{red}根
根的结点。
2)当n >1时,其余结点可分为m (m>0)个
互不相交的有限集合
\color{red}互不相交的有限集合
互不相交的有限集合
T
1
,
T
2
,
.
…
,
T
m
T_1, T_2,.…, Tm
T1,T2,.…,Tm,其中每个集合本身又是一棵树,并且称为根结点的
子树
\color{red}子树
子树。
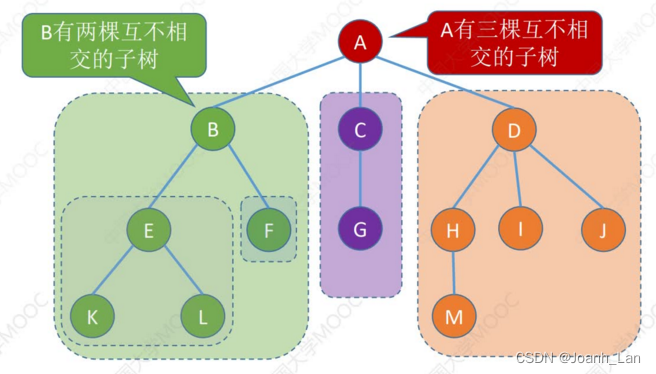
树是一种递归定义的数据结构 \color{green}树是一种递归定义的数据结构 树是一种递归定义的数据结构
二叉树
\color{red}二叉树
二叉树:一个分支结点
最多只能有两棵子树
\color{red}最多只能有两棵子树
最多只能有两棵子树
树
\color{red}树
树:一个分支结点
可以有多棵子树
\color{red}可以有多棵子树
可以有多棵子树
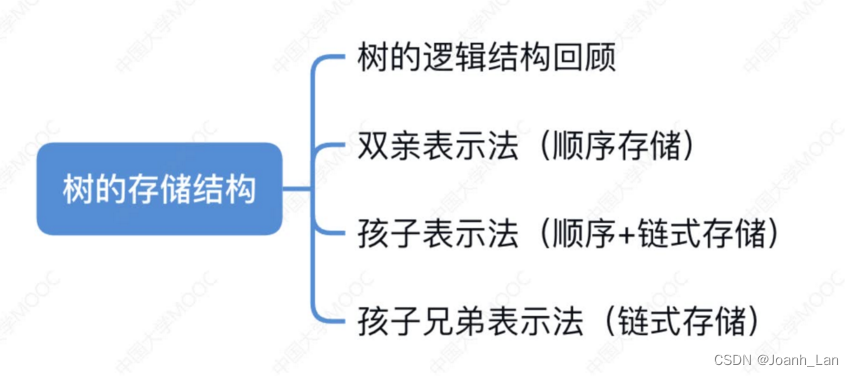
对的顺序存储
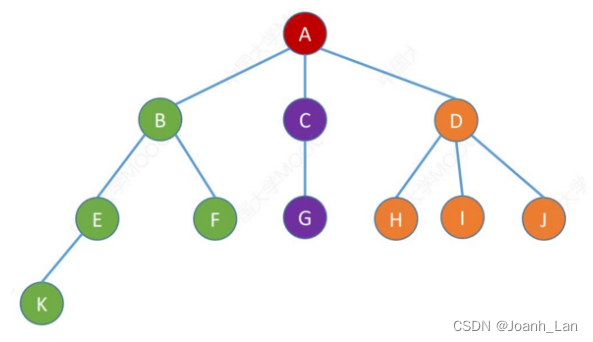

树
\color{red}树
树:一个分支结点
可以有多棵子树
\color{red}可以有多棵子树
可以有多棵子树
只依靠数组下标,无法反映结点之间的逻辑关系
\color{red}只依靠数组下标,无法反映结点之间的逻辑关系
只依靠数组下标,无法反映结点之间的逻辑关系
思路:用数组顺序存储各个结点。每个结点中保存 数据元素、指向双亲结点 ( 父节点)的“指针” \color{red}数据元素、指向双亲结点(父节点)的“指针” 数据元素、指向双亲结点(父节点)的“指针”
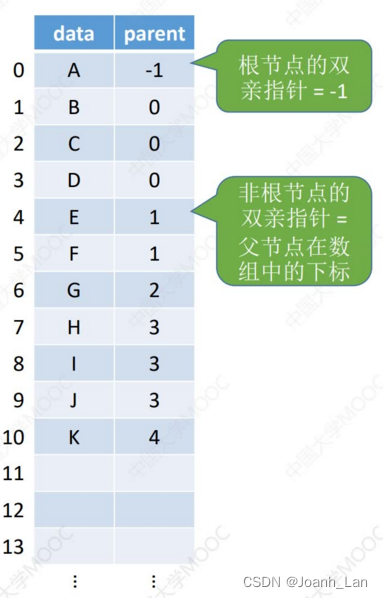
#define MAX_TREE_SIZE 100
typedef struct
{
ElemType data;
int parent; //双亲位置域
}PTNode;
typedef struct
{
PTNode nodes[MAX_TREE_SIZE];
int n; //结点数
}PTree;
拓展:双亲表示法存储“森林”
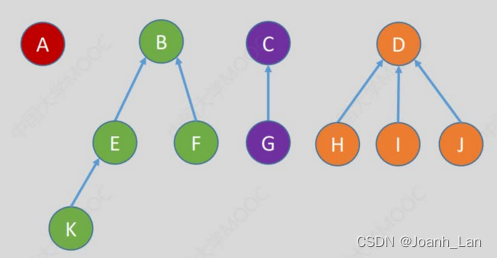

双亲表示法的优缺点
双亲表示法
\color{red}双亲表示法
双亲表示法
优点
:
找双亲(父节点)很方便
\color{red}优点:找双亲(父节点)很方便
优点:找双亲(父节点)很方便
缺点
:
找孩子不方便,只能从头到尾遍历整个数组
\color{red}缺点:找孩子不方便,只能从头到尾遍历整个数组
缺点:找孩子不方便,只能从头到尾遍历整个数组
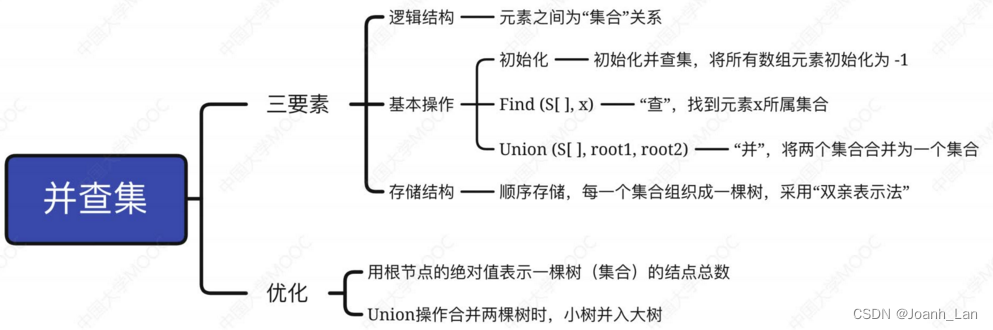
适用于“找父亲”多,“找孩子”少的应用场景。如:并查集
树的存储2:孩子表示法
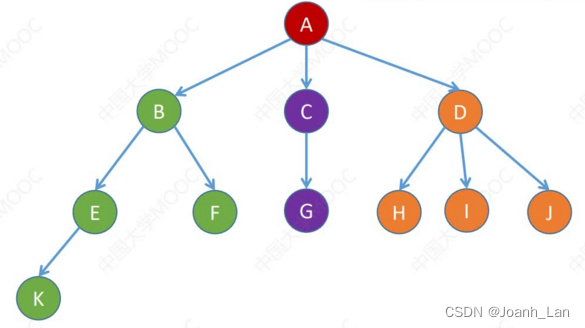
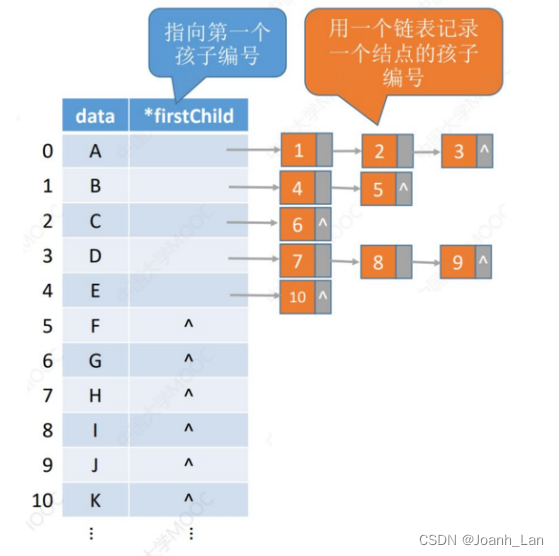
孩子表示法:用数组顺序存储各个结点。每个结点中保存 数据元素、孩子链表头指针 \color{red}数据元素、孩子链表头指针 数据元素、孩子链表头指针
顺序存储 + 链式存储结合 \color{green}顺序存储+链式存储结合 顺序存储+链式存储结合
#define MAX_TREE_SIZE 100
struct CTNode
{
int chile; //孩子结点在数组中的位置
struct CTNode* next;
};
typedef struct
{
ElemType data;
struct CTNode *firstChile; //第一个孩子
}CTBox;
typedef struct
{
CTBox nodes[MAX_TREE_SIZE];
int n, r; //结点总数 & 根的位置
}CTree;
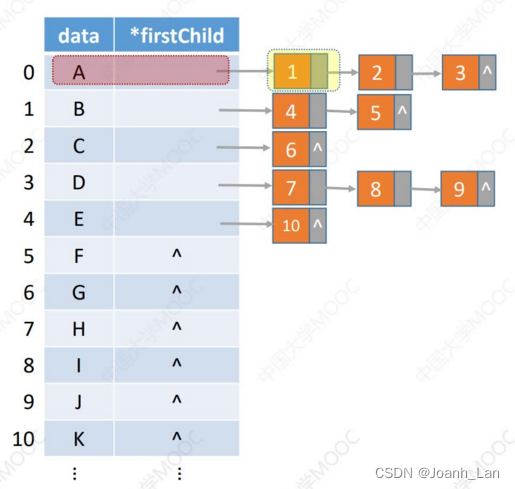
拓展:孩子表示法存储“森林”
森林。森林是m (m≥0)棵互不相交的树的集合
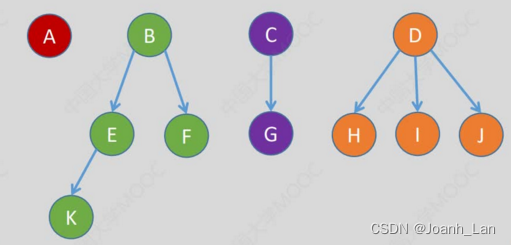
注:用孩子表示法存储森林,需要记录多个根的位置
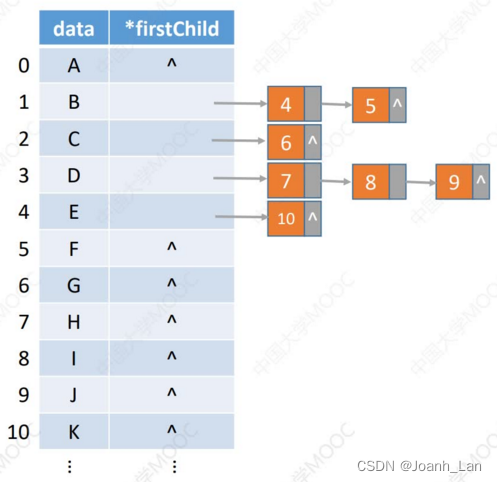
孩子表示法的优缺点
孩子表示法
优点
:
找孩子很方便
\color{red}优点:找孩子很方便
优点:找孩子很方便
缺点
:
找双亲
(
父节点)不方便,只能遍历每个链表
\color{red}缺点:找双亲(父节点)不方便,只能遍历每个链表
缺点:找双亲(父节点)不方便,只能遍历每个链表
适用于“找孩子”多,“找父亲”少的应用场景。如 : 服务流程树 \color{green}适用于“找孩子”多,“找父亲”少的应用场景。如:服务流程树 适用于“找孩子”多,“找父亲”少的应用场景。如:服务流程树
树的存储3:孩子兄弟表示法
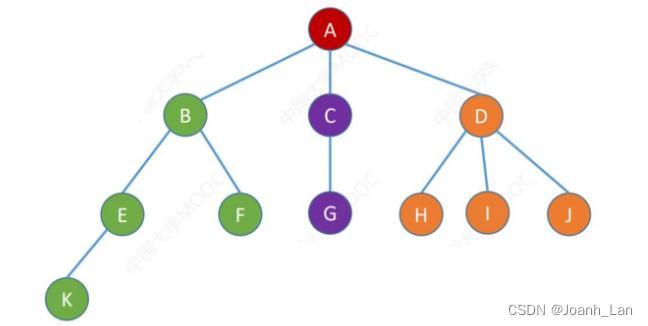
typedef struct CSNode
{
ElemType data;
struct CSNode *firstchile, *nextsibling; //第一个孩子和右兄弟指针
} CSNode, *CSTree;
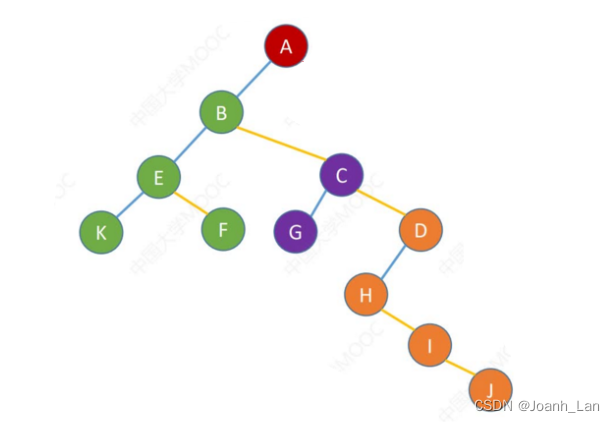
孩子兄弟表示法 ==>
拓展:孩子兄弟表示法存储森林
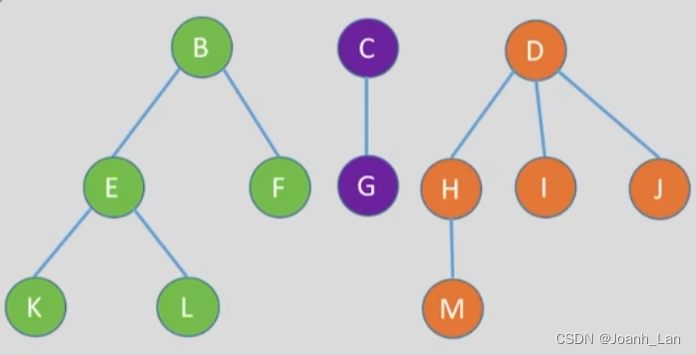
孩子兄弟表示法 ==>
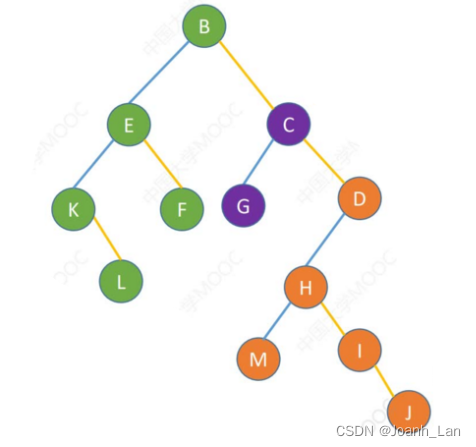
当使用“孩子兄弟表示法”存储树或森林时,从存储视角来看 形态上与二叉树类似 \color{red}形态上与二叉树类似 形态上与二叉树类似。
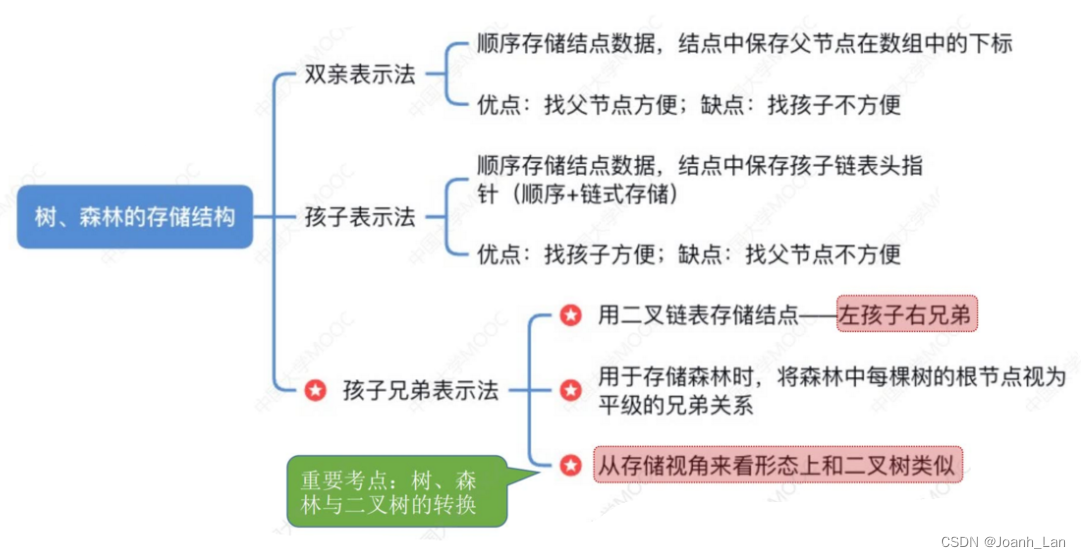
知识点回顾与重要考点




![[工业互联-23]:EtherCat从站 - EtherCAT协议栈与工作原理, 软硬件解决方案](https://img-blog.csdnimg.cn/img_convert/4f598be158a91d5620fb840e1900a897.png)
![LeetCode[394]字符串解码](https://img-blog.csdnimg.cn/a75939e3a17b4c9a965f188720012317.png)