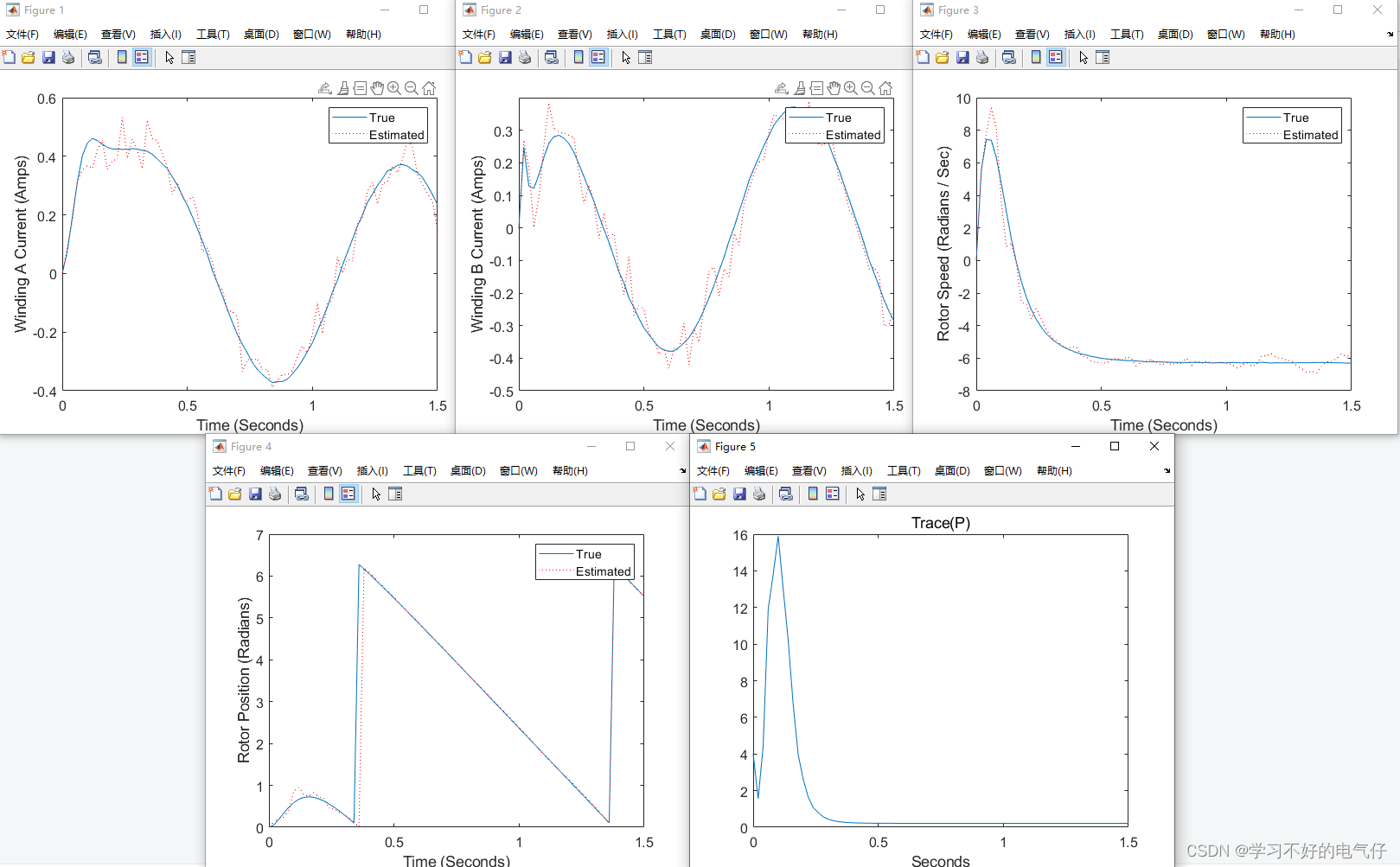
两相步进电机的连续时间延长卡尔曼滤波器仿真, 根据定子电流的噪声测量,估计定子电流以及转子位置和速度。
主程序:
function MotorKalman
% 两相步进电机的连续时间延长卡尔曼滤波器仿真
% 根据定子电流的噪声测量,估计定子电流以及转子位置和速度
Ra = 1.9; % 绕组电阻
L = 0.003; % 绕组电感
lambda = 0.1; % 电机常数
J = 0.00018; % 转动惯量
B = 0.001; % 粘性摩擦系数
ControlNoise = 0.01; % std dev of uncertainty in control inputs
AccelNoise = 0.5; % std dev of shaft acceleration noise
MeasNoise = 0.1; % standard deviation of measurement noise
R = [MeasNoise^2 0; 0 MeasNoise^2]; % Measurement noise covariance
xdotNoise = [ControlNoise/L ControlNoise/L 0.5 0];
Q = [xdotNoise(1)^2 0 0 0; 0 xdotNoise(2)^2 0 0; 0 0 xdotNoise(3)^2 0; 0 0 0 xdotNoise(4)^2]; % Process noise covariance
P = 1*eye(4); % Initial state estimation covariance
dt = 0.0005; % Integration step size
tf = 1.5; % Simulation length
x = [0; 0; 0; 0]; % Initial state
xhat = x; % State estimate
w = 2 * pi; % Control input frequency
dtPlot = 0.01; % How often to plot results
tPlot = -inf;
% Initialize arrays for plotting at the end of the program
xArray = [];
xhatArray = [];
trPArray = [];
tArray = [];
% Begin simulation loop
for t = 0 : dt : tf
if t >= tPlot + dtPlot
% Save data for plotting
tPlot = t + dtPlot - eps;
xArray = [xArray x];
xhatArray = [xhatArray xhat];
trPArray = [trPArray trace(P)];
tArray = [tArray t];
end
% Nonlinear simulation
ua0 = sin(w*t);
ub0 = cos(w*t);
xdot = [-Ra/L*x(1) + x(3)*lambda/L*sin(x(4)) + ua0/L;
-Ra/L*x(2) - x(3)*lambda/L*cos(x(4)) + ub0/L;
-3/2*lambda/J*x(1)*sin(x(4)) + 3/2*lambda/J*x(2)*cos(x(4)) - B/J*x(3);
x(3)];
xdot = xdot + [xdotNoise(1)*randn; xdotNoise(2)*randn; xdotNoise(3)*randn; xdotNoise(4)*randn];
x = x + xdot * dt;
x(4) = mod(x(4), 2*pi);
% Kalman filter
F = [-Ra/L 0 lambda/L*sin(xhat(4)) xhat(3)*lambda/L*cos(xhat(4));
0 -Ra/L -lambda/L*cos(xhat(4)) xhat(3)*lambda/L*sin(xhat(4));
-3/2*lambda/J*sin(xhat(4)) 3/2*lambda/J*cos(xhat(4)) -B/J -3/2*lambda/J*(xhat(1)*cos(xhat(4))+xhat(2)*sin(xhat(4)));
0 0 1 0];
H = [1 0 0 0; 0 1 0 0];
z = H * x + [MeasNoise*randn; MeasNoise*randn];
xhatdot = [-Ra/L*xhat(1) + xhat(3)*lambda/L*sin(xhat(4)) + ua0/L;
-Ra/L*xhat(2) - xhat(3)*lambda/L*cos(xhat(4)) + ub0/L;
-3/2*lambda/J*xhat(1)*sin(xhat(4)) + 3/2*lambda/J*xhat(2)*cos(xhat(4)) - B/J*xhat(3);
xhat(3)];
xhat = xhat + xhatdot * dt;
Pdot = F * P + P * F' + Q - P * H' * inv(R) * H * P;
P = P + Pdot * dt;
K = P * H' * inv(H * P * H' + R);
xhat = xhat + K * (z - H * xhat);
xhat(4) = mod(xhat(4), 2*pi);
end
作图程序:
close all;
figure;
plot(tArray, xArray(1,:), tArray,xhatArray(1,:),'r:')
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Time (Seconds)'); ylabel('Winding A Current (Amps)');
legend('True', 'Estimated');
figure;
plot(tArray, xArray(2,:), tArray,xhatArray(2,:),'r:')
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Time (Seconds)'); ylabel('Winding B Current (Amps)');
legend('True', 'Estimated');
figure;
plot(tArray, xArray(3,:), tArray,xhatArray(3,:),'r:')
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Time (Seconds)'); ylabel('Rotor Speed (Radians / Sec)');
legend('True', 'Estimated');
figure;
plot(tArray, xArray(4,:), tArray,xhatArray(4,:),'r:')
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Time (Seconds)'); ylabel('Rotor Position (Radians)');
legend('True', 'Estimated');
figure;
plot(tArray, trPArray); title('Trace(P)', 'FontSize', 12);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('Seconds');误差计算程序:
N = size(xArray, 2);
N2 = round(N / 2);
xArray = xArray(:,N2:N);
xhatArray = xhatArray(:,N2:N);
iaEstErr = sqrt(norm(xArray(1,:)-xhatArray(1,:))^2 / size(xArray,2));
ibEstErr = sqrt(norm(xArray(2,:)-xhatArray(2,:))^2 / size(xArray,2));
wEstErr = sqrt(norm(xArray(3,:)-xhatArray(3,:))^2 / size(xArray,2));
thetaEstErr = sqrt(norm(xArray(4,:)-xhatArray(4,:))^2 / size(xArray,2));
disp(['Std Dev of Estimation Errors = ',num2str(iaEstErr),', ',num2str(ibEstErr),', ',num2str(wEstErr),', ',num2str(thetaEstErr)]);
% Display the P version of the estimation error standard deviations
disp(['Sqrt(P) = ',num2str(sqrt(P(1,1))),', ',num2str(sqrt(P(2,2))),', ',num2str(sqrt(P(3,3))),', ',num2str(sqrt(P(4,4)))]);
运行结果: