八数码问题

每个局面是三行三列的数字方阵，每个位置为0-8的一个数码且互不相同，求从初始局面（自己设定）如何“最快”移动到终止局面（自己设定）。

移动规则：每次只能0与其上下左右四个方向相邻的某个数字交换！可能有解，可能无解。

如下例子：

起始矩阵                  目标矩阵
0	1	2		?		1	2	3
3	4	5		=》		4	5	6
6	7	8				7	8	0

如上所示例子，从起始矩阵 到 目标矩阵，如果可达的话，其中的路径有很多条；当然也有不可达的情况。要求的程序就是要识别这两种情况，可达就求出最短路径；不可达就给出提示。

程序当中使用的结构体：

typedef struct QDatatype
{
	int* arr; // 存储状态矩阵
	struct QueueNode* father; // 该结点的上一个路径的结点下标
	int deap; // 当前结点所在路径的深度
}QDatatype;

// 队列的链式结构实现
typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* head_tail;
	QueueNode* tail;
	int size;
}Queue;

如上:Queue为队列的指针域，QueueNode为队列当中每一个结点当中存储的指针和数据域，QDatatype为队列当中每一个结点的数据域。

 判断两个矩阵是否可达

 

首先我们可以确定的是，给定的 起始状态 和 目标状态是用 3 x 3 矩阵来进行存储的。那么我们可以先来了解一个概念：

一个矩阵的逆置值，通常也称为矩阵的行列式（determinant），是一个与矩阵中元素顺序相关的标量值。当我们交换矩阵中的两个元素时，会导致矩阵中元素的顺序发生改变，这可能会导致矩阵的逆置值发生变化。

更具体地说，让我们考虑一个2x2的矩阵，设其元素为a、b、c和d，其逆置值为det。根据矩阵行列式的定义，det的值为ad-bc。

当我们交换矩阵中第一行和第二行的元素时，得到的新矩阵为：

c d

a b

它的行列式为：cb-da。 显然，此时行列式的值与原矩阵的行列式ad-bc不同。

因此，交换矩阵中任意两个元素的位置，都可能会导致矩阵的逆置值发生变化。这也是为什么在计算行列式时，需要根据矩阵中元素的位置来计算逆置值。

那么对于矩阵当中的元素进行交换的时候，这个矩阵的逆置值可能会发生改变，由上所述：
为了确定这两个矩阵的可达性，可以使用起始矩阵的奇偶性以及目标矩阵的奇偶性来进行判断。这是因为八数码问题中，每一次合法操作都会改变矩阵奇偶性的值，因此，起始矩阵和目标矩阵的奇偶性不同，则它们之间不存在可达路径。

因为合法操作通常包括将空格上、下、左、右四个方向之一的数字移动到空格的位置上，这会导致逆序对的数量发生变化。如果原序列中的逆序对数量为奇数，那么根据定义，操作后的逆序对数量一定为偶数；如果原序列中的逆序对数量为偶数，那么操作后的逆序对数量一定为奇数。因此，每一次合法操作都会改变矩阵的奇偶性。

而使用逆序对来计算一个矩阵的逆置值（行列式），这是一种标准的计算方法。

所以，我们可以 起始矩阵和 目标矩阵 所对应的 逆序对数（逆置值）的奇偶性是否相同，相同表示 两个矩阵可达；如果奇偶性不相等那就说明，两个矩阵之间不相等。

接下来，问题就好解决了，只用求解一个矩阵当中有多少对逆序对就行了，关于逆序对的定义就是在一个序列中，如果存在两个元素a[i]和a[j]，其中i<j且a[i]>a[j]，那么我们称这两个元素构成一个逆序对。

对于一个矩阵，我们可以将其按行或者按列展开成一个一维数组（序列），然后计算这个一维数组中的逆序对数量。

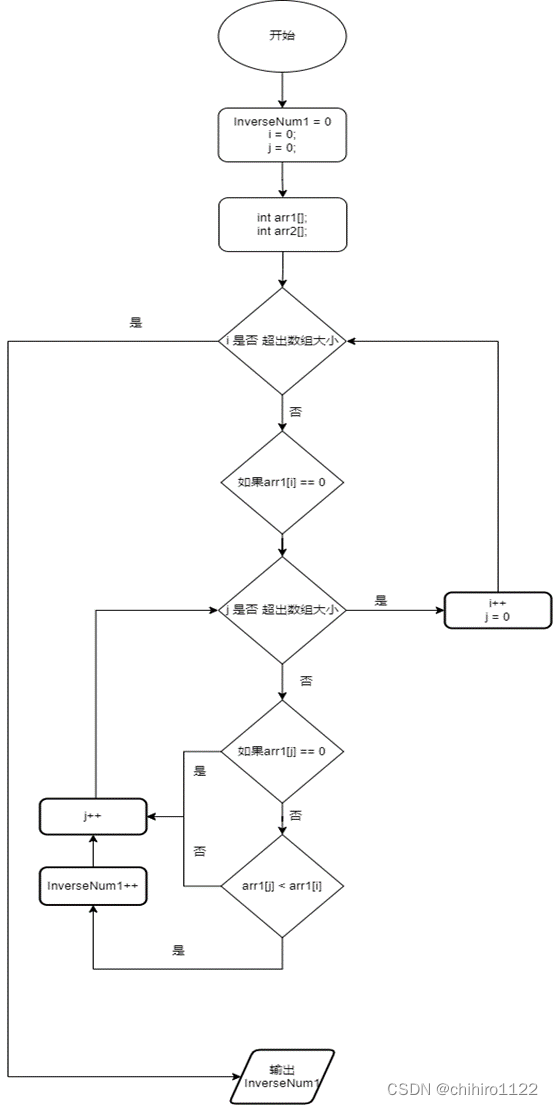
求矩阵逆置的流程图：

 

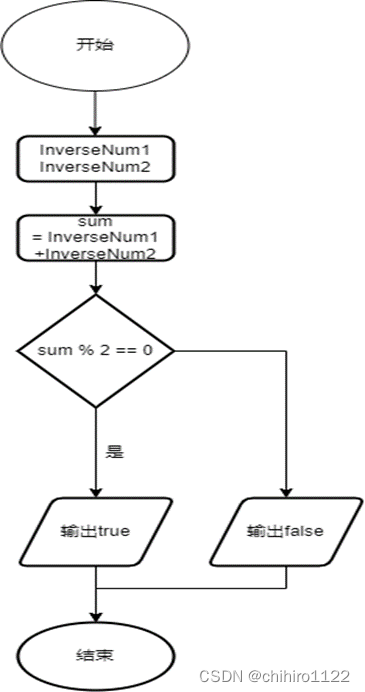
求两个矩阵逆置值的奇偶性是否相等的流程图：
 

 完整代码：

bool matrix_is_arrive(int* arr1, int* arr2, int row, int wide)
{
	int InverseNum1 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
	
		if (arr1[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
		
			if (arr1[j] == 0)
				continue;

			if (arr1[i] > arr1[j])
				InverseNum1++;
		}
	}

	int InverseNum2 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
	
		if (arr2[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
		
			if (arr2[j] == 0)
				continue;

			if (arr2[i] > arr2[j])
				InverseNum2++;
		}
	}


	if ((InverseNum2 + InverseNum1) % 2 == 0)
		return true;
	else
		return false;
}

解决重复值问题

 对于数阵问题，根本上就是深度和广度的搜索，虽然以深度和广度都可以搜索出来，但是深度的广度的效率低下，因为在依次找最短路径的过程当中就会找到很多的重复的或者是不需要的“没用的”的结点，那么这个结点的个数是远超出我们想象的。可能最短路径为20步的路径，假设使用广度的话需要多遍历好几十倍甚至更多的结点，而且这只是保守估计。

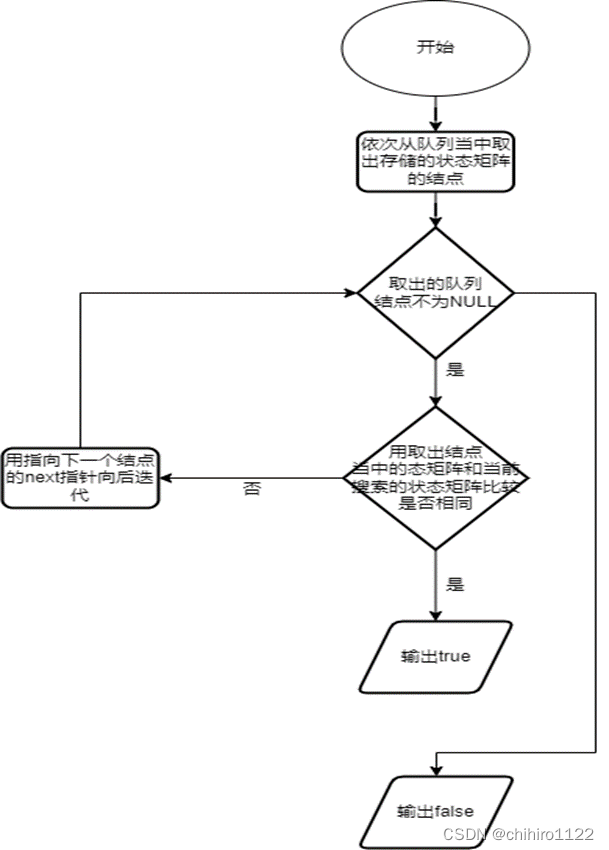
广度优先搜索算法当中使用的是队列来实现，那么对于广度优先搜索算法，简单来说就是把搜索过的结点入队，那么我们可以在队列当中来进行全局遍历，也就是从一个父亲结点找出一个孩子结点（从一个结点找出这个结点在 3 x 3 的地图上可以走的位置）之后，那么就查看这个走之后的生成的状态矩阵是否在 队列当中 存在，如果存在，说明当前搜索出的结点，是之前已经搜索过的重复结点，那么就直接跳过这个结点不把这个结点入队。如果当前搜索出的结点没有在 队列 当中出现过的话，说明这个结点没有被搜索过，可以入队。以上就解决了 在搜索过程当中 搜索出重复值之后 如果进行判断，判断当前搜索出的结点是否是 已经搜索过的重复值。

因为程序当中使用的是链式队列，所以遍历这个队列只需要依次访问当前结点的 next 指针即可，就像单链表的遍历一样。

流程图：

 

bool is_same(QueueNode* Node1, int* arr)
{
	for (int j = 0; j < 9; j++)
	{
		if (Node1->data.arr[j] != arr[j])
		{
			return false;
		}
	}

	return true;
}

// A* 当中判断是否搜索过的函数

bool is_in_close(Queue* open, int* arr)
{
	QueueNode* tmp = open->head;
	while (tmp != open->head_tail)
	{
		if (is_same(tmp, arr))
		{
			return true;
		}
		tmp = tmp->next;
	}

	return false;
}


QueueNode* is_in_open(Queue* open, int* arr)
{
	QueueNode* tmp = open->head_tail;
	while (tmp)
	{
		if (is_same(tmp, arr))
		{
			return tmp;
		}
		tmp = tmp->next;
	}

	return NULL;
}

// 广度当中使用的判断是否搜索过的函数

// 判断在 close 队列当中是否有状态和当前状态是否相同
bool is_in_st(Queue* close, int* arr)
{
	QueueNode* tmp = close->head;
	while(tmp)
	{
		if (is_same(tmp , arr))
		{
			return true;
		}
		tmp = tmp->next; 
	}

 上述的open 和 close 是可以看做是两个队列，对于这两个队列，会在下述详细描述 广度优先搜索和 A* 基于广度优先搜索的启发式算法当中进行详细说明。

1. 和路径输出问题

程序当中的广度优先搜索是从一个父亲结点来找出这个父亲结点的满足条件的，可以走的结点，那么从父亲结点到孩子结点就是一条路径。因为广度优先搜索是一层一层往下搜索路径的，所以，只要广度优先搜索找到了目标，那么这目标对应的路径就是最短路径。这是广度优先搜索的好处。所以，我们只需要在每一次从某一个父亲结点搜索其孩子结点的时候，如果这个孩子入队了，说明这个路径是可以走的，那么就把这个孩子结点当中 指向父亲结点的 father 指针指向 当前的父亲结点就可以完成路径的链接了。

在上述当中判断当前结点在队列当中是否有搜索过这个问题当中给出了队列的结构体的实现，其中的数据就有一个 father 指针，这个指针就是用于存储这个 结点 父亲结点，那么到最后，依次链接。最后，只需要在 队列当中找到 目标结点，这个结点一定只有一个，然后根据这个结点的 father 指针就可以找到最短路径了。

1. 广度优先搜索算法

上述也说了一些广度优先的实现，主要思想就是利用队列“先进先出”的特性，首先，把起始结点入队，从这个起始结点开始找这个结点的孩子结点。把这个父亲结点的所有可以走的路径走过之后，因为出队。然后下一次就从队头取结点，从这个结点再去找出这个结点可以走的子节点，找完之后再把这个父亲结点出队，这是广度查找的基本思想。

当这个结点所有可以走的孩子结点都入队之后，说明这个父亲结点的所有可以走的路径都已经搜索完了，那么按照一般的广度优先搜索算法来说，应该把这个父亲结点出队，因为这个结点已经搜索过了，但是，因为在八数码当中有，有非常多的重复结点的情况，这个父亲结点就算已经被搜索过了，应该出队，但是出队之后，如果在之后搜索当中，搜索出了和这个父亲结点的状态矩阵相同的状态矩阵，这是不允许的。

因为就算是这个父亲结点在八数码问题当中，是属于在搜索过程当中查找过的结点，这个结点搜索出的矩阵，之后再搜索过程当中就不能再出现了。

所以，以上的矛盾，解决办法就是在创建一个队列close，这个队列用于存储从原本队列（open）当中出队的结点，这样我们就不会丢失从open队列当中出队的状态矩阵了。

但是如果向上实现的话，就会有一个问题：我们之前说过的，我们从搜索过的路径当中找到最短路径，是从最后开始，通过最短路径当中的每一个结点的 father 指针来依次往前来寻找，打印出路径，那么我们在出队的时候一般是会释放掉这个结点对应的空间的，然后，当我们在close 当中入队的时候，只是和新的结点当中存储的是一起从open 当中出队的结点当中的数据，所以当我们释放掉这个结点空间，也就意味着，这个结点的孩子结点的father原本存储的是这个结点的地址，但是这个结点空间已经释放了，也就是说此时孩子结点的 father 指针存储空间地址已经失效了，所以综上所述，就会出现链接问题。

当然处理办法有很多，首先最暴力的就是不释放open原本要出队的结点空间，因为本程序的使用的队列是链式队列，可以直接修改链接关系，达到在不释放当前结点的空间的前提下，从open队列当中出队，从close 队列当中入队。

本程序实现的把open队列和close队列合并为一个队列，使用三个指针分别是 指向close队列队头的 head指针，指向open队列队头的指针 head_tail 指针和 执行open队列队尾的tail 指针来进行维护。具体关系如下所示：

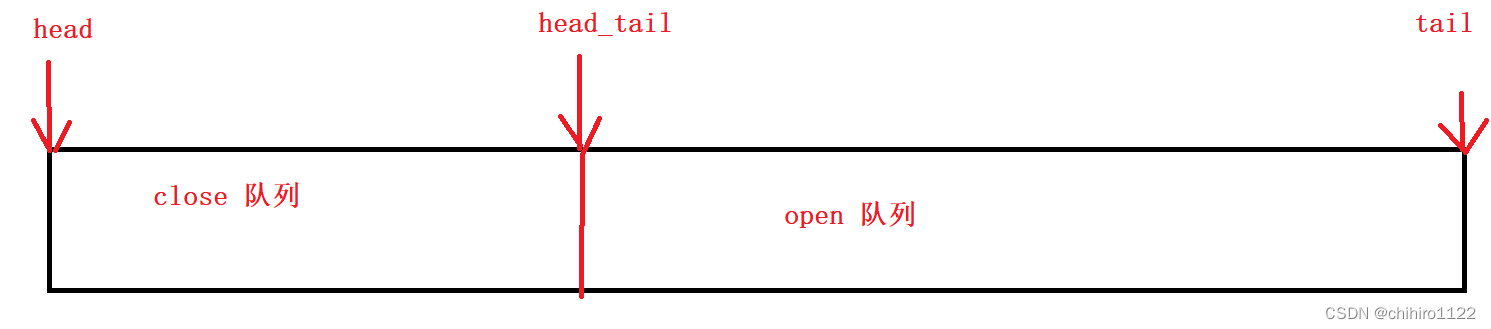
使用如上所示的好处就是，我不需要改链接关系，每一次进行上述的出队入队的操作，只需要把 head_tail 指针往后移动就可以实现，

本程序实现的广度优先主要分为两大块，首先是外层的大循环，外层循环当中实现的是：每一次从某一个父亲结点搜索完所有的孩子结点之后，判断搜索出的并且入队的状态矩阵当中有没有出现目标结点的情况，如果出现了，就跳出循环；如果没有出现，就会执行第二块：把当前队头结点作为父亲结点，寻找这个父亲结点所以可以走的 孩子结点，入队，然后把父亲结点从open当中出队，入队到close当中，和上述差不多。

在第二块当中会以 上下左右 四个方向依次寻找，先判断移动的坐标是否合法，然后判断在close队列和open队列当中是否出现，没出现就入队，修改father指针链接关系，出现就跳过这个孩子结点的搜索，进行下一个孩子搜索，当搜索完之后，head_tail 指针往后移动，实现出队和入队操作。

当然在，在执行广度优先搜索之前，要先判断这个例子是否可达，不可达直接结束，可达在进行求解。

 广度优先搜索板块的代码(其中某些函数将会在完整代码当中给出)：

// 广度优先算法 函数
void BFS(QueueNode* node , Queue* open)
{

	int blake = 0;
		// 找到空格的下标
		for (int i = 0; i < 9; i++)
		{
			if (node->data.arr[i] == 0)
			{
				blake = i;
				break;
			}
		}
		int dx = INT_MAX;
		// 向上走
		dx = blake - 3;
		if (dx >= 0)
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);
	
			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}
	
		//向下走
		dx = blake + 3;
		if (dx < 9)
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}

	
		//向左走
		dx = blake - 1;
		if (dx >= (3 * (blake / 3)))
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}
	
		//向右走
		dx = blake + 1;
		if (dx < (3 * (blake / 3 + 1)))
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}

		// open 表当中存储的路径，把不是路径的结点 出open
		// 入队到 close 当中，表示这个结点已经被搜索过了

		open->head_tail = open->head_tail->next;

}

int main()
{
		int numStart[] = {1,0,2,6,7,5,4,8,3};

		int numEnd[] = { 1,2,3,4,5,0,6,7,8};

	//	int numStart[] = { 2, 8, 3,
	//		1, 6, 4,
	//		7, 0, 5 };
	//int numEnd[] = { 1, 2, 3,
	//	7, 8, 4,
	//	0, 6, 5 };

	Queue open;
	QueueInit(&open);

	// 判断起始矩阵 和 最终矩阵是否可达
	printf("矩阵是否可达（0 / 1）:%d", matrix_is_arrive(numStart, numEnd, 3, 3));

	QDatatype* tmp = creat_Node(numStart, NULL , 0);
	QueueNode* tmpNode = QueuePush(&open, tmp);

	open.head_tail = open.head;

	//Queue close; 
	//QueueInit(&close);

	// 首先计算 初始矩阵和 目标矩阵是否可达
	if (matrix_is_arrive(numStart, numEnd, 3, 3))
	{
		// open 队列不为空就继续 在 open 队列当中加入这个 结点能走的子节点
		while (!QueueEmpty(&open))
		{
			if (is_in_st(&open, numEnd))
				break;
			// 广度优先遍历算法函数
			BFS(open.head_tail , &open); // 求解八数码问题
		}
	}
	else
	{
		printf("不可达!!!");
	}


	return 0;
}

1. A*算法实现

 

A* 算法和之前的广度优先算法本质上没有多大区别，只是在每一次BFS 函数选取结点的时候，并不是盲目的从open的头结点来取，而且选取open队列当中全部结点当中，选出一个权值最小的结点，来作为BFS 搜索的父亲结点，这样就大大减少了BFS 函数在搜索过程当中所多搜索出来的重复的，无意义的结点。

而这个权值是什么我们先不谈，我们先谈BFS函数当中如何对这个搜索的父亲结点的各个孩子结点 赋上权值。

在单纯的广度优先搜索当中，只是单纯的在 open表和close表当中寻找是否有重复的状态矩阵存在；而在 A* 当中，不是单纯的判断了，要把open队列和close队列分开判断，首先，如果在close当中出现，那么就直接跳过这个方向的搜索，如果没有在close当中出现过，也没有在open当中出现，那么就直接入队（open和close 的合并队列）；如果close当中没有出现，open当中出现了，那么也就是说，我们可能需要修改open当中这个重复的结点的存储的数据和连接信息，如果当前新搜索的孩子结点的权值计算出来，比open当中重复结点的权值小，说明当前搜索出来的是更好的路径结点，那么就把这个结点替换掉open队列当中的重复结点。

以上就是A*主要过程。

接下来是如何计算权值，上述也说过了，当我们需要把一个孩子结点入队的时候，我需要计算这个孩子结点的权值，这样才能实现后面用权值来选择我要搜索的父亲结点。那么本程序当中的权值有两部分组成：h(n) 表示当前状态矩阵和 起始矩阵的之间路径的深度；g(n) 表示的是当前状态矩阵当中的每一个元素到达目标元素位置所差的横纵标距离之和，也就是把每一个元素的所差的横纵坐标距离之和加起来，作为这个状态矩阵的 g(n) 权值。那么，最终这个状态矩阵的权值表示为 p(n) = h(n) + g(n) 。其中p(n) 就是我所使用的权值，这个权值就是 h(n) 和 g(n) 的和。本程序当中的权值计算使用的是嵌套循环来求权值。

接下来是处理，open 队列 和 close 队列的问题，在A* 当中因为搜索的父亲结点不再是盲目的选取 open 队列的头结点，而且从open 队列当中找权值最小的，那么这也就意味着，我每一次找完一个父亲结点的所以可以走的孩子之后，需要把这个父亲结点从open队列当中取出来，入队到 close 队列当中，但是这个父亲结点不一定是open的队头结点，所以，如果这个父亲结点是open队列的中间结点，那么从open队列当中取出这个元素我需要修改这个父亲结点在 open 当中的链接关系。因为这里使用的链式栈，单项链表不在适用，所以这适用双向链表的形式来实现。

修改之后的结构体如下：

typedef struct QDatatype
{
	int* arr; // 存储状态矩阵
	struct QueueNode* father; // 该结点的上一个路径的结点下标
	int deap; // 当前结点所在路径的深度
}QDatatype;

// 队列的链式结构实现

typedef struct QueueNode
{
	int end_distance; // 当前结点的到目标结点的 估计权值
	struct QueueNode* next; // 下一个结点的指针
	struct QueueNode* above; // 上一个结点的指针
	QDatatype data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* head_tail;
	QueueNode* tail;
	int size_open;  // 维护 open 表的元素个数
	int size_close; // 维护 close 表的元素个数
}Queue;

上述也说过了，队列当中的 head_tail 指针是指向open 队列的第一个结点，那么这个head_tail 指向结点的上一个结点就是 close 队列的最后一个结点，所以我们可以以此来向close当中尾插数据。

A*算法当中和广度一样，分为两大块，首先是外层的大循环，和广度为底层的搜索函数。

 A* 启发函数计算权值代码：
 

int Manhattan_distance( int* Arr, int* numArr)
{
	int distance = 0;
	int flag = 0;

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			flag = 0;
			for (int k = 0; k < 3; k++)
			{
				for (int m = 0; m < 3; m++)
				{
					if (Arr[i * 3 + j] == numArr[k * 3 + m])
					{
						distance += abs(i - k) + abs(j - m);
						flag = 1;
						break;
					}
				}
				if (flag == 1)
					break;
			}
		}
	}
	return distance;
}

从存储搜索过的矩阵的队列当中取出权值最小的结点（状态矩阵）的代码：

QueueNode* GetMin_distance_Node(QueueNode* pq)
{
	int distance = INT_MAX;
	QueueNode* tmp = pq, *returnNode = NULL;
	while (tmp != NULL)
	{
		// 除去已经 搜索过的结果
		if (tmp->end_distance == INT_MAX)
			continue;

		if ((tmp->data.deap + tmp->end_distance) < distance)
		{
			returnNode = tmp;
			distance = tmp->data.deap + tmp->end_distance;
		}

		tmp = tmp->next;
	}

	return returnNode;
}

程序的输入输出

 

本程序当中主要使用A*算法来实现数阵问题，在A*计算最短路径算法的基础之上，写了一些面向对象的菜单，和输出格式；还有随机生成 起始矩阵和 目标矩阵进行求解和 在文件当中输入一个或者多个例子 ，然后再屏幕上统一输出的两个方式进行和用户的交互。

首先是程序的菜单流程图如下所示（如图9所示）：

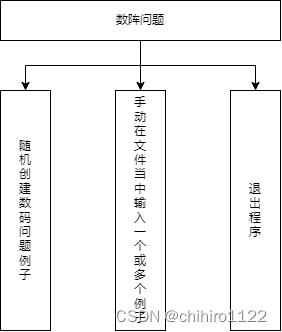
框架流程图-图9

菜单在屏幕上的打印如下图所示（如图10所示）：

程序菜单-图10

输入1，随机生成数阵问题的例子，然后求解打印在屏幕上，下述当中给了随机生成的可以走和不可走的例子（如下图11和图12 和图13 所示）：

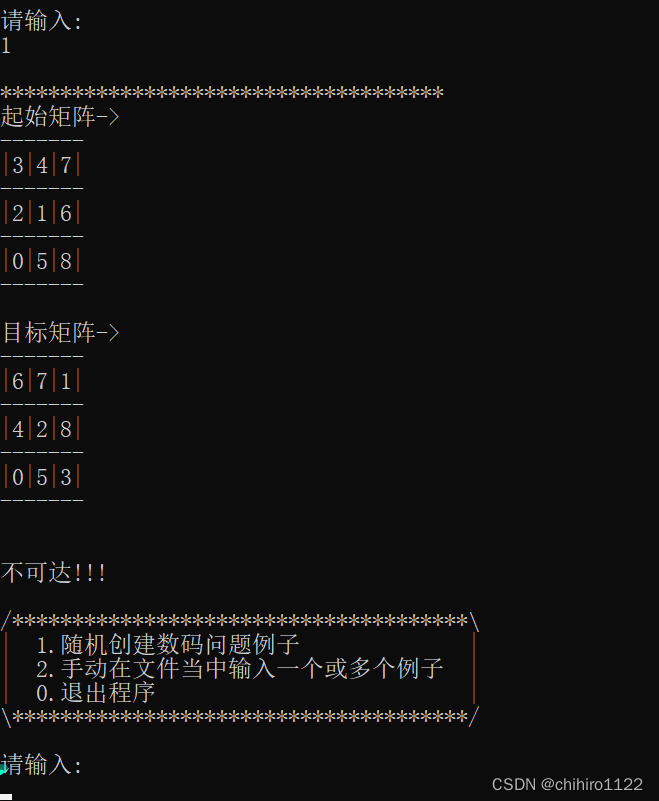
不可达的例子图-图11

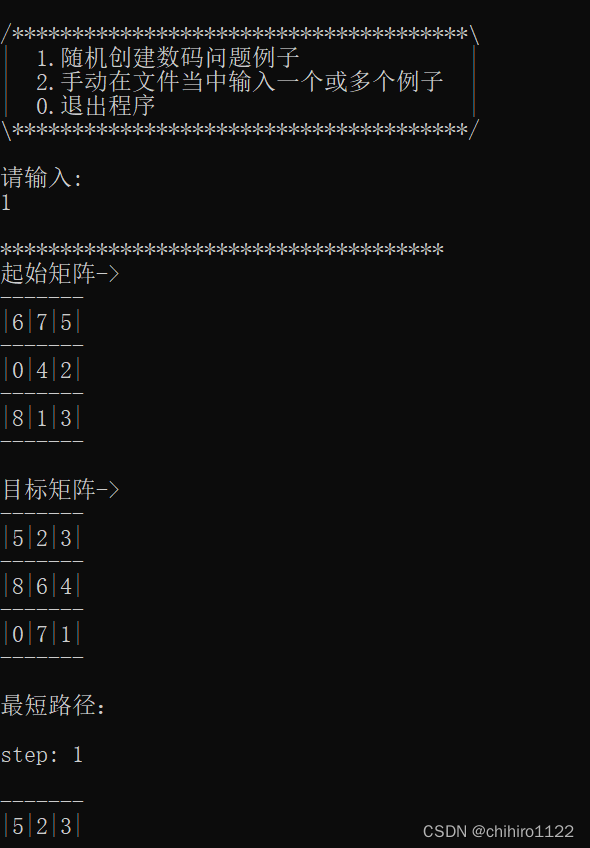
可达的例子图1-图12

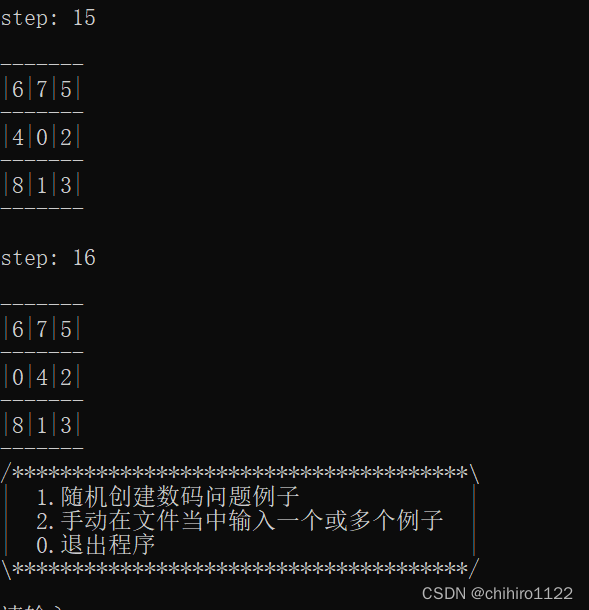
可达的例子图2-图13

上述当中的中间路径过多，不在截图展示，只展示开头和结尾。

如上就是随机生成例子，然后求解这个例子，再打印在屏幕上的过程。

文件输入。可以输入一个或者多个例子，每一个矩阵为一行，第一个起始矩阵，第二个是目标矩阵，依此类推。多个例子不需要用什么符号分割，只需要在之前例子之后令其一行按照上述所属的输入即可。具体在文件当中的输入格式如下图所示（如图14所示）：

单个例子输入：

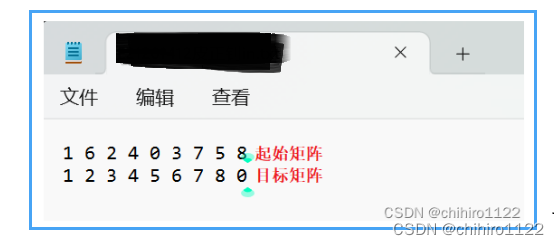
单个例子输入示意图-图14

如上所示，矩阵当中的元素和元素之间用 空格进行分割；矩阵和矩阵之间用 行进行分割

单个例子在屏幕上的输出（如图15和图16一样）：

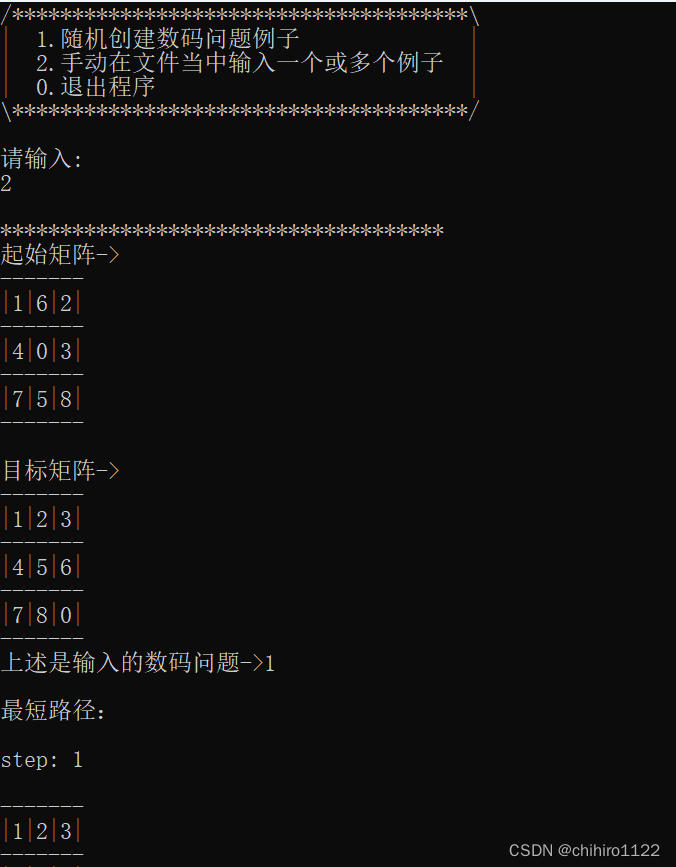
单个例子输出示意图1-图15

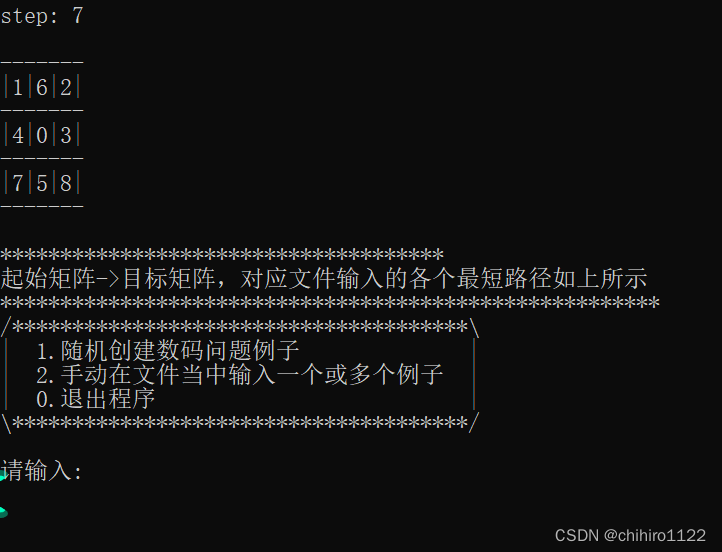
单个例子输出示意图2-图16

同样，上述只给出了开头和结尾的示意图。

多个例子的输入（如图17所示）：

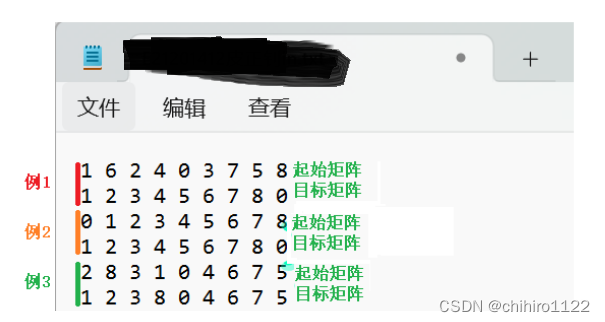
多个例子的输入格式如上所示-图17

输出和单个例子如出一致，只是不同的例子的路径用下图所示的方式进行分割（如图18所示）：

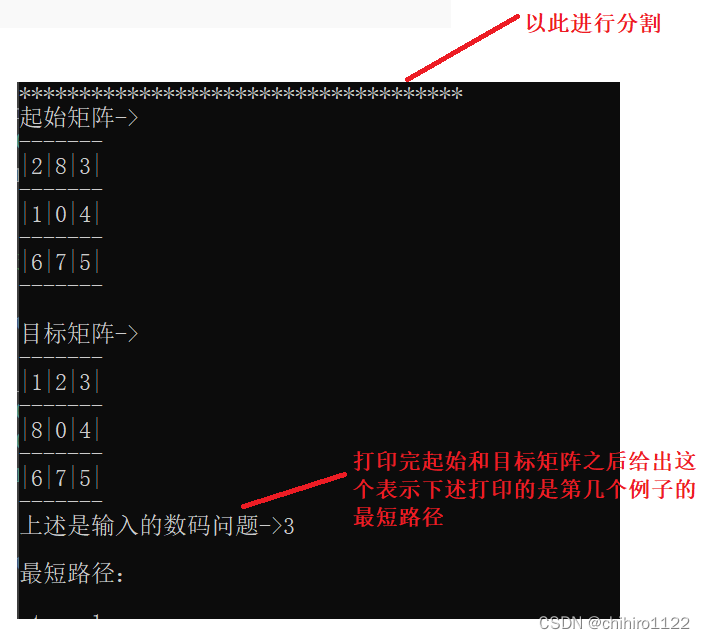
多个例子输出部分示意图-图18

 程序完整代码

 广度优先搜索代码

 

#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>

typedef struct QDatatype
{
	int* arr; // 存储状态矩阵
	struct QueueNode* father; // 该结点的上一个路径的结点下标
	int deap; // 当前结点所在路径的深度
}QDatatype;

// 队列的链式结构实现

typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* head_tail;
	QueueNode* tail;
	int size;
}Queue;

// 队列的初始化
void QueueInit(Queue* pq);
// 队列的销毁
void QueueDestroy(Queue* pq);
// 队列的插入
QueueNode* QueuePush(Queue* pq, QDatatype* x);
// 队列删除缘元素
void QueuePop(Queue* pq);
// 判断队列是否为空
bool QueueEmpty(Queue* pq);
// 拿到队头的数据
QDatatype QueueFront(Queue* pq);

// 队列的初始化
void QueueInit(Queue* pq)
{
	assert(pq);

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

// 队列的销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);

	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur->next;
	}

	pq->head = pq->tail = NULL;
	pq->size = 0;
}


// 队列的插入
QueueNode* QueuePush(Queue* pq, QDatatype* x)
{
	assert(pq);

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	newNode->data.arr = (int*)malloc(sizeof(int) * 9);
	if (newNode == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	newNode->next = NULL;
	for (int i = 0; i < 9; i++)
	{
		newNode->data.arr[i] = x->arr[i];
	}
	newNode->data.deap = x->deap;
	newNode->data.father = x->father;


	if (pq->head == NULL)
	{
		assert(pq->tail == NULL);

		pq->head = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}

	pq->size++;
	return newNode;
}

// 队列删除缘元素
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head);

	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QueueNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}

// 判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->size == 0;
}

// 拿到队头的数据
QDatatype QueueFront(Queue* pq)
{
	assert(pq);

	return pq->head->data;
}



// 判断两个状态是否相同
bool is_same(QueueNode* Node1, int* arr)
{
		for (int j = 0; j < 9; j++)
		{
			if (Node1->data.arr[j] != arr[j])
			{
				return false;
			}
		}

		return true;
}

bool is_same1(int* arr2, int* arr)
{
	for (int j = 0; j < 9; j++)
	{
		if (arr2[j] != arr[j])
		{
			return false;
		}
	}

	return true;
}

// 判断在 close 队列当中是否有状态和当前状态是否相同
bool is_in_st(Queue* close, int* arr)
{
	QueueNode* tmp = close->head;
	while(tmp)
	{
		if (is_same(tmp , arr))
		{
			return true;
		}
		tmp = tmp->next; 
	}

	return false;
}

// 交换两个结点的函数
void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

QDatatype* creat_Node(int* a , struct QueueNode* father ,int deap)
{
	QDatatype* tmp = (QDatatype*)malloc(sizeof(QDatatype));
	tmp->arr = (int*)malloc(sizeof(int) * 9);
	for (int i = 0; i < 9; i++)
	{
		tmp->arr[i] = a[i];
	}
	tmp->father = father;
	tmp->deap = deap;

	return tmp;
}

int tmpArr[9];

// 广度优先算法 函数
void BFS(QueueNode* node , Queue* open)
{

	int blake = 0;
		// 找到空格的下标
		for (int i = 0; i < 9; i++)
		{
			if (node->data.arr[i] == 0)
			{
				blake = i;
				break;
			}
		}
		int dx = INT_MAX;
		// 向上走
		dx = blake - 3;
		if (dx >= 0)
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);
	
			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}
	
		//向下走
		dx = blake + 3;
		if (dx < 9)
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}

	
		//向左走
		dx = blake - 1;
		if (dx >= (3 * (blake / 3)))
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}
	
		//向右走
		dx = blake + 1;
		if (dx < (3 * (blake / 3 + 1)))
		{
			for (int i = 0; i < 9; i++)
			{
				tmpArr[i] = node->data.arr[i];
			}
			Swap(&tmpArr[blake], &tmpArr[dx]);

			// 判断交换之后的 矩阵是否重复
			// 判断 open 队列 和 close 队列当中是否有当前状态矩阵
			// 如果没有就把这个状态矩阵入队
			if (!is_in_st(open, tmpArr))
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->data.father = node;
			}
		}

		// open 表当中存储的路径，把不是路径的结点 出open
		// 入队到 close 当中，表示这个结点已经被搜索过了

		open->head_tail = open->head_tail->next;

}




// 判断起始矩阵和 最终矩阵是否可达，
// 参数：              起始矩阵  最终矩阵    矩阵长    矩阵宽
bool matrix_is_arrive(int* arr1, int* arr2 , int row , int wide)
{
	int InverseNum1 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
		// 跳过0
		if (arr1[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
			// 跳过0 
			if (arr1[j] == 0)
				continue;

			if (arr1[i] > arr1[j])
				InverseNum1++;
		}
	}

	int InverseNum2 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
		// 跳过0
		if (arr2[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
			// 跳过0
			if (arr2[j] == 0)
				continue;

			if (arr2[i] > arr2[j])
				InverseNum2++;
		}
	}

	// 判断奇偶性是否相同
	if ((InverseNum2 + InverseNum1) % 2 == 0)
		return true;
	else
		return false;
}

QueueNode* EndNode(Queue* Qe, int* numEnd)
{
	QueueNode* tmp = Qe->head;
	while (tmp)
	{
		if (is_same(tmp, numEnd))
		{
			return tmp;
		}
		tmp = tmp->next;
	}

	return NULL;
}

// 输出路径
void Print(QueueNode* node)
{
	QueueNode* tmp = node;
	int num = 1;
	while (tmp != NULL)
	{
		printf("step: %d\n",num++);
		for (int i = 0; i < 9; i++)
		{
			printf("%d", tmp->data.arr[i]);
			if ((i + 1) % 3 == 0)
			{
				printf("\n");
			}
		}
		//printf("\n");
		tmp = tmp->data.father;
	}
}


int main()
{
		int numStart[] = {1,0,2,6,7,5,4,8,3};

		int numEnd[] = { 1,2,3,4,5,0,6,7,8};

	//	int numStart[] = { 2, 8, 3,
	//		1, 6, 4,
	//		7, 0, 5 };
	//int numEnd[] = { 1, 2, 3,
	//	7, 8, 4,
	//	0, 6, 5 };

	Queue open;
	QueueInit(&open);

	// 判断起始矩阵 和 最终矩阵是否可达
	printf("矩阵是否可达（0 / 1）:%d", matrix_is_arrive(numStart, numEnd, 3, 3));

	QDatatype* tmp = creat_Node(numStart, NULL , 0);
	QueueNode* tmpNode = QueuePush(&open, tmp);

	open.head_tail = open.head;

	//Queue close; 
	//QueueInit(&close);

	// 首先计算 初始矩阵和 目标矩阵是否可达
	if (matrix_is_arrive(numStart, numEnd, 3, 3))
	{
		// open 队列不为空就继续 在 open 队列当中加入这个 结点能走的子节点
		while (!QueueEmpty(&open))
		{
			if (is_in_st(&open, numEnd))
				break;
			// 广度优先遍历算法函数
			BFS(open.head_tail , &open); // 求解八数码问题
		}

		// 在open 队列当中找到目标结点的位置
		QueueNode* EndNumNode = EndNode(&open, numEnd);

		printf("\n最短路径：\n");
		// 输出路径函数
		Print(EndNumNode);
	}
	else
	{
		printf("不可达!!!");
	}


	return 0;
}

A*算法代码

 

#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<time.h>

typedef struct QDatatype
{
	int* arr; 
	struct QueueNode* father; 
	int deap;
}QDatatype;

// 队列的链式结构实现

typedef struct QueueNode
{
	int end_distance; 
	struct QueueNode* next; 
	struct QueueNode* above; 
	QDatatype data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* head_tail;
	QueueNode* tail;
	int size_open;  
	int size_close;
}Queue;


QueueNode* GetMin_distance_Node(QueueNode* pq)
{
	int distance = INT_MAX;
	QueueNode* tmp = pq, *returnNode = NULL;
	while (tmp != NULL)
	{
		// 除去已经 搜索过的结果
		if (tmp->end_distance == INT_MAX)
			continue;

		if ((tmp->data.deap + tmp->end_distance) < distance)
		{
			returnNode = tmp;
			distance = tmp->data.deap + tmp->end_distance;
		}

		tmp = tmp->next;
	}

	return returnNode;
}

int Manhattan_distance( int* Arr, int* numArr)
{
	int distance = 0;
	int flag = 0;

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			flag = 0;
			for (int k = 0; k < 3; k++)
			{
				for (int m = 0; m < 3; m++)
				{
					if (Arr[i * 3 + j] == numArr[k * 3 + m])
					{
						distance += abs(i - k) + abs(j - m);
						flag = 1;
						break;
					}
				}
				if (flag == 1)
					break;
			}
		}
	}
	return distance;
}


QueueNode* QueuePush(Queue* pq, QDatatype* x)
{
	assert(pq);

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	newNode->data.arr = (int*)malloc(sizeof(int) * 9);
	if (newNode == NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	newNode->next = NULL;
	newNode->above = NULL;
	for (int i = 0; i < 9; i++)
	{
		newNode->data.arr[i] = x->arr[i];
	}
	newNode->data.deap = x->deap;
	newNode->data.father = x->father;

	if (pq->head == NULL)
	{
		assert(pq->tail == NULL);

		pq->head = pq->head_tail = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		newNode->above = pq->tail;
		pq->tail = newNode;
	}

	pq->size_open++;
	return newNode;
}

void QueueOpenPop(Queue* pq , QueueNode* node)
{
	assert(pq);
	assert(pq->head);
	assert(pq->head_tail);

	if (node == pq->head_tail)
	{
		pq->head_tail = pq->head_tail->next;
	}
	else
	{
		if (pq->tail == node)
			pq->tail = pq->tail->above;

		QueueNode* next = node->next;
		QueueNode* above = node->above;
		above->next = next;
		if(next)
			next->above = above;

		pq->head_tail->above->next = node;
		node->next = pq->head_tail;
		node->above = pq->head_tail->above;
		pq->head_tail->above = node;
	}

	pq->size_open--;
	pq->size_close++;
}


bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->size_open == 0;
}

void QueueInit(Queue* pq)
{
	assert(pq);

	pq->head = pq->head_tail = pq->tail = NULL;
	pq->size_open = 0;
	pq->size_close = 0;
}

int count = 0;

bool is_same(QueueNode* Node1, int* arr)
{
	for (int j = 0; j < 9; j++)
	{
		if (Node1->data.arr[j] != arr[j])
		{
			return false;
		}
	}

	return true;
}


bool is_in_close(Queue* open, int* arr)
{
	QueueNode* tmp = open->head;
	while (tmp != open->head_tail)
	{
		if (is_same(tmp, arr))
		{
			return true;
		}
		tmp = tmp->next;
	}

	return false;
}


QueueNode* is_in_open(Queue* open, int* arr)
{
	QueueNode* tmp = open->head_tail;
	while (tmp)
	{
		if (is_same(tmp, arr))
		{
			return tmp;
		}
		tmp = tmp->next;
	}

	return NULL;
}

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}


QDatatype* creat_Node(int* a, struct QueueNode* father, int deap)
{
	QDatatype* tmp = (QDatatype*)malloc(sizeof(QDatatype));
	tmp->arr = (int*)malloc(sizeof(int) * 9);
	for (int i = 0; i < 9; i++)
	{
		tmp->arr[i] = a[i];
	}
	tmp->father = father;
	tmp->deap = deap;

	return tmp;
}

int tmpArr[9];


void BFS(QueueNode* node, Queue* open , int* numEnd)
{

	int blake = 0;

	for (int i = 0; i < 9; i++)
	{
		if (node->data.arr[i] == 0)
		{
			blake = i;
			break;
		}
	}
	int dx = INT_MAX;

	dx = blake - 3;
	if (dx >= 0)
	{
		for (int i = 0; i < 9; i++)
		{
			tmpArr[i] = node->data.arr[i];
		}
		Swap(&tmpArr[blake], &tmpArr[dx]);


		int distance = Manhattan_distance(tmpArr, numEnd);

		if (!is_in_close(open, tmpArr))
		{
			QueueNode* tmpNode = is_in_open(open, tmpArr);
			if (!tmpNode)
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->end_distance = distance;
			}
			else
			{
	
				if (tmpNode->end_distance + tmpNode->data.deap > distance + node->data.deap + 1)
				{
					tmpNode->data.deap = node->data.deap + 1;
					tmpNode->data.father = node;
					tmpNode->end_distance = distance;
				}
			}
		}
	}

	
	dx = blake + 3;
	if (dx < 9)
	{
		for (int i = 0; i < 9; i++)
		{
			tmpArr[i] = node->data.arr[i];
		}
		Swap(&tmpArr[blake], &tmpArr[dx]);

	
		int distance = Manhattan_distance(tmpArr, numEnd);

		if (!is_in_close(open, tmpArr))
		{
			QueueNode* tmpNode = is_in_open(open, tmpArr);
			if (!tmpNode)
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->end_distance = distance;
			}
			else
			{
			
				if (tmpNode->end_distance + tmpNode->data.deap > distance + node->data.deap + 1)
				{
					tmpNode->data.deap = node->data.deap + 1;
					tmpNode->data.father = node;
					tmpNode->end_distance = distance;
				}
			}
		}
	}



	dx = blake - 1;
	if (dx >= (3 * (blake / 3)))
	{
		for (int i = 0; i < 9; i++)
		{
			tmpArr[i] = node->data.arr[i];
		}
		Swap(&tmpArr[blake], &tmpArr[dx]);


		int distance = Manhattan_distance(tmpArr, numEnd);

		if (!is_in_close(open, tmpArr))
		{
			QueueNode* tmpNode = is_in_open(open, tmpArr);
			if (!tmpNode)
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->end_distance = distance;
			}
			else
			{
		
				if (tmpNode->end_distance + tmpNode->data.deap > distance + node->data.deap + 1)
				{
					tmpNode->data.deap = node->data.deap + 1;
					tmpNode->data.father = node;
					tmpNode->end_distance = distance;
				}
			}
		}
	}


	dx = blake + 1;
	if (dx < (3 * (blake / 3 + 1)))
	{
		for (int i = 0; i < 9; i++)
		{
			tmpArr[i] = node->data.arr[i];
		}
		Swap(&tmpArr[blake], &tmpArr[dx]);


		int distance = Manhattan_distance(tmpArr, numEnd);

		if (!is_in_close(open, tmpArr))
		{
			QueueNode* tmpNode = is_in_open(open, tmpArr);
			if (!tmpNode)
			{
				QDatatype* tmp = creat_Node(tmpArr, node, node->data.deap + 1);
				QueuePush(open, tmp);

				open->tail->end_distance = distance;
			}
			else
			{

				if (tmpNode->end_distance + tmpNode->data.deap > distance + node->data.deap + 1)
				{
					tmpNode->data.deap = node->data.deap + 1;
					tmpNode->data.father = node;
					tmpNode->end_distance = distance;
				}
			}
		}
	}



	QueueOpenPop(open, node);

}


bool matrix_is_arrive(int* arr1, int* arr2, int row, int wide)
{
	int InverseNum1 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
	
		if (arr1[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
		
			if (arr1[j] == 0)
				continue;

			if (arr1[i] > arr1[j])
				InverseNum1++;
		}
	}

	int InverseNum2 = 0;
	for (int i = 0; i < row * wide - 1; i++)
	{
	
		if (arr2[i] == 0)
			continue;

		for (int j = i + 1; j < row * wide; j++)
		{
		
			if (arr2[j] == 0)
				continue;

			if (arr2[i] > arr2[j])
				InverseNum2++;
		}
	}


	if ((InverseNum2 + InverseNum1) % 2 == 0)
		return true;
	else
		return false;
}


QueueNode* EndNode(Queue* Qe, int* numEnd)
{
	QueueNode* tmp = Qe->head;
	while (tmp)
	{
		if (is_same(tmp, numEnd))
		{
			return tmp;
		}
		tmp = tmp->next;
	}

	return NULL;
}


void Print(QueueNode* node)
{
	QueueNode* tmp = node;
	int num = 1;
	while (tmp != NULL)
	{
		printf("\nstep: %d\n\n-------\n", num++);
		for (int i = 0; i < 9; i++)
		{
			printf("|%d", tmp->data.arr[i]);
			if ((i + 1) % 3 == 0)
			{
				printf("|\n-------\n");
			}
		}

		tmp = tmp->data.father;
	}
}


void Eight_difital_A(int* numStart, int* numEnd)
{
	Queue open;
	QueueInit(&open);

	QDatatype* tmp = creat_Node(numStart, NULL, 0);
	QueueNode* tmpNode = QueuePush(&open, tmp);

	if (matrix_is_arrive(numStart, numEnd, 3, 3))
	{

		while (!QueueEmpty(&open))
		{
			if (is_in_open(&open, numEnd))
				break;


			QueueNode* node = GetMin_distance_Node(open.head_tail);

			BFS(node, &open, numEnd);
		}

	
		QueueNode* EndNumNode = EndNode(&open, numEnd);

		printf("\n最短路径：\n");
	
		Print(EndNumNode);
	}
	else
	{
		printf("\n\n不可达!!!\n\n");
	}
}

void menu()
{
	printf("/**************************************\\\n");
	printf("|  1.随机创建数码问题例子              |\n");
	printf("|  2.手动在文件当中输入一个或多个例子  |\n");
	printf("|  0.退出程序                          |\n");
	printf("\\**************************************/\n\n请输入:\n");
}

bool digital_is_same_rand(int pos, int num ,int* arr)
{
	for (int i = 0; i < pos; i++)
	{
		if (num == arr[i])
			return true;
	}

	return false;
}

int main()
{
	int numStart[9];
	int numEnd[9];
	FILE* f1 = fopen("xxxx.txt", "r");
	int returnnum = 1, size = 0;

	int num = 1;
	while (num)
	{
		menu();
		scanf("%d", &num);
		switch (num)
		{
			case 1:
				printf("\n*************************************\n起始矩阵->");
				srand((unsigned)time(NULL));
				for (int i = 0; i < 9; i++)
				{
					numStart[i] = rand() % 9;
					while (digital_is_same_rand(i, numStart[i], numStart))
					{
						numStart[i] = rand() % 9;
					}
					if (i % 3 == 0 && i != 0)
						printf("|");
					if (i % 3 == 0)
						printf("\n-------\n");
					printf("|%d", numStart[i]);
				}
				printf("|\n-------\n\n目标矩阵->");
				for (int i = 0; i < 9; i++)
				{
					numEnd[i] = rand() % 9;
					while (digital_is_same_rand(i, numEnd[i], numEnd))
					{
						numEnd[i] = rand() % 9;
					}
					if (i % 3 == 0 && i != 0)
						printf("|");
					if (i % 3 == 0)
						printf("\n-------\n");
					printf("|%d", numEnd[i]);
				}
				printf("|\n-------\n");

				Eight_difital_A(numStart, numEnd);
				break;
			case 2:
				while (returnnum != EOF)
				{
					size++;
					printf("\n*************************************\n起始矩阵->");
					for (int i = 0; i < 9; i++)
					{
						returnnum = fscanf(f1, "%d ", &numStart[i]);

						if (returnnum == EOF)
							break;

						if (i % 3 == 0 && i != 0)
							printf("|");
						if (i % 3 == 0)
							printf("\n-------\n");
						printf("|%d", numStart[i]);
					}
					if (returnnum == EOF)
					{
						printf("目标矩阵，对应文件输入的各个最短路径如上所示\n*******************************************************\n");
						break;
					}
					printf("|\n-------\n\n目标矩阵->");
					for (int i = 0; i < 9; i++)
					{
						fscanf(f1, "%d ", &numEnd[i]);
						if (i % 3 == 0 && i != 0)
							printf("|");
						if (i % 3 == 0)
							printf("\n-------\n");
						printf("|%d", numEnd[i]);
					}
					printf("|\n-------\n上述是输入的数码问题->%d\n", size);

					Eight_difital_A(numStart, numEnd);
				}
				break;
			default :
				break;
		}
	}
	fclose(f1);

	return 0;
}