搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

思路

暴力解法

有时候暴力解法并不一定会超时，要看怎么样去遍历。
这题很简单，由于已经排好序了，直接从小到大遍历一遍，只要发现比target大的数，就返回当前下标。
如果没有找到，说明target是数组里面最大的数，返回数组长度。
代码如下：

int searchInsert(vector<int>& nums, int target) {  
  
    for(int i=0; i<nums.size(); i++)  
    {  
        if(nums[i] >= target)  
            return i;  
    }  
    return nums.size();  
}

时间复杂度：O（n）
空间复杂度：O(1)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Q4SdTur1-1688979259280)(/imgs/2023-07-10/BcnAbYhRLWxm7lu4.png)]

二分法

这道题的二分法也非常简单，我的思路是：按照正常的全闭合区间二分查找，如果找到了返回下标便是，如果找不到则返回当前的left。
为什么是返回当前的left？
我们知道全闭合的二分查找的终止条件为（left <= right），也就是最后出来循环的是left +1。
我们给出一个例子

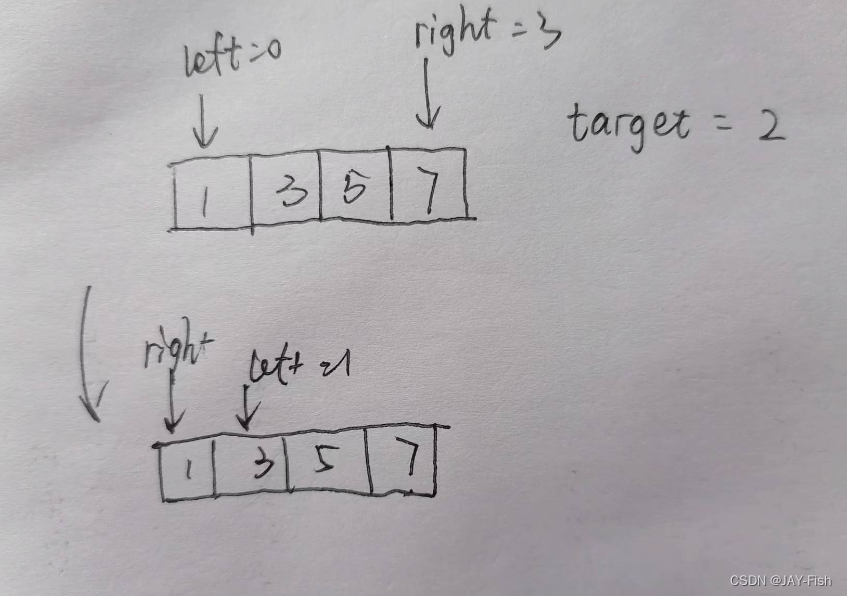
在这里插入图片描述

可以看出最后的结果是left = 1，right = 0，因此循环不满足条件而退出。
所以最后返回的应该是left（也可以是right +1 ）
代码如下

  
int searchInsert(vector<int>& nums, int target) {  
    int left=0,right = nums.size()-1;  
    int mid;  
    while(left <= right)  
    {  
        mid = (left + right)>>1;  
        if(nums[mid] > target)  
        {  
            right = mid -1 ;  
        }else if(nums[mid] < target)  
        {  
            left = mid + 1;  
        }else{  
            return mid;  
        }  
    }  
    return left;  
}