1.简述

      计算概率分布律及密度函数值

matlab直接提供了通用的计算概率密度函数值的函数，它们是pdf 和namepdf函数，使用方式如下：
Y=pdf(‘name’，K，A，B)或者：namepdf (K，A，B)
上述函数表示返回在X=K处、参数为A、B、C的概率值或密度值，对于不同的分布，参数个数是不同；name为分布函数名，使用时需要按照对应分布进行改动。函数名总结如下表：

name的取值    函数说明
‘beta’ 或 ‘Beta’    Beta分布
‘bino’ 或 ‘Binomial’    二项分布
‘chi2’ 或 ‘Chisquare’    卡方分布
‘exp’ 或 ‘Exponential’    指数分布
‘f’ 或 ‘F’    F分布
‘gam’ 或 ‘Gamma’    GAMMA分布
‘geo’ 或 ‘Geometric’    几何分布
‘hyge’ 或 ‘Hypergeometric’    超几何分布
‘logn’ 或 ‘Lognormal’    对数正态分布
‘nbin’ 或 ‘Negative Binomial’    负二项式分布
‘ncf’ 或 ‘Noncentral F’    非中心F分布
‘nct’ 或 ‘Noncentral t’    非中心t分布
‘ncx2’ 或 ‘Noncentral Chi-square’    非中心卡方分布
‘norm’ 或 ‘Normal’    正态分布
‘poiss’ 或 ‘Poisson’    泊松分布
‘rayl’ 或 ‘Rayleigh’    瑞利分布
‘t’ 或 ‘T’    T分布
‘unif’ 或 ‘Uniform’    连续均匀分布
‘unid’ 或 ‘Discrete Uniform’    离散均匀分布
‘weib’ 或 ‘Weibull’    Weibull分布
 

2.代码及运行结果

%%  二项分布的密度函数
clear all;
x=1:20;
y=binopdf(x,200,0.06); 
figure;
plot(x,y,'r*');
title('二项分布（n=200，p=0.06）');

%%  泊松分布的密度函数
clear all;
x=1:20;
y=poisspdf(x,20);       %泊松分布
figure;
plot(x,y,'r+');
title('泊松分布');

 

%%   几何分布
clear all;
x=1:10;
y=geopdf(x,0.4);        %几何分布
figure;
plot(x,y,'rx');
title('几何分布');

 

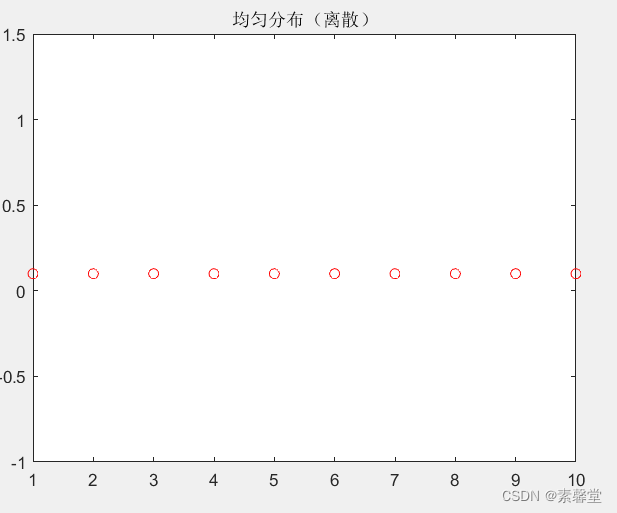
%%  均匀分布（离散）
clear all;
n=10;
x=1:n;
y=unidpdf(x,n);             %均匀分布（离散）
figure;
plot(x,y,'ro');
title('均匀分布（离散）');

 

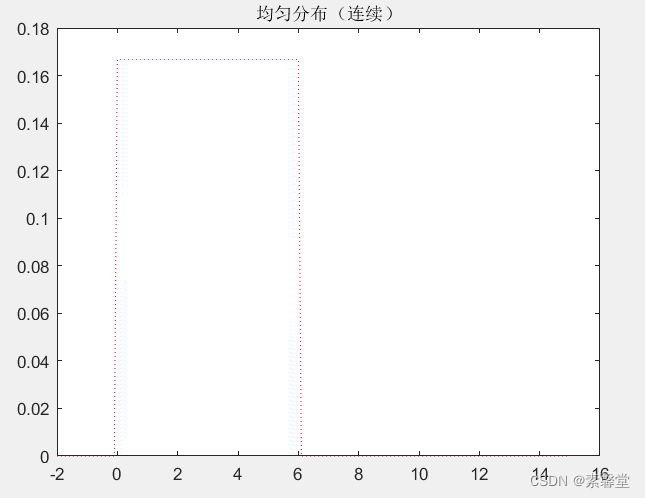
%%  均匀分布（连续）
clear all;
x=-2:0.1:15;
y=unifpdf(x,0,6);           %均匀分布（连续）   0到6之间
figure;
plot(x,y,'r:');
title('均匀分布（连续）');

 

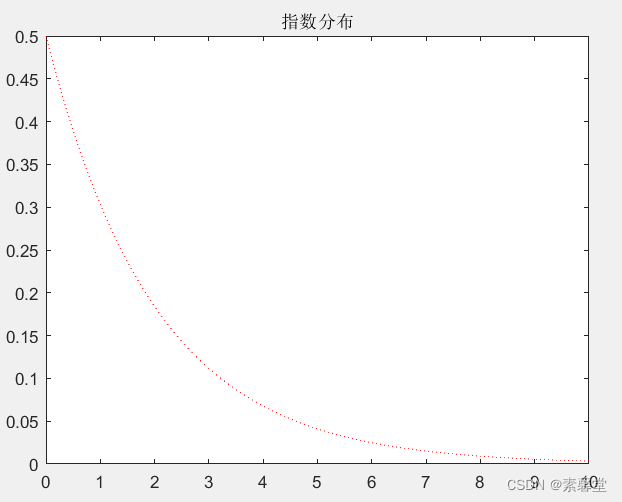
%%  指数分布
clear all;
x=0:0.1:10;
y=exppdf(x,2);      %指数分布
figure;
plot(x,y,'r:');
title('指数分布');

 

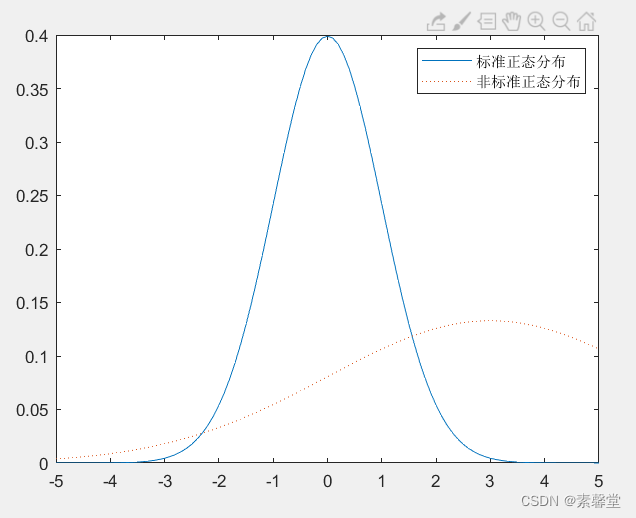
%%  正态分布
clear all;
x=-5:0.1:5;
y1=normpdf(x,0,1);          %标准正态分布
y2=normpdf(x,3,3);          %非标准正态分布
figure;
plot(x,y1,x,y2,':');
legend('标准正态分布','非标准正态分布');
x1=-5:0.1:5;
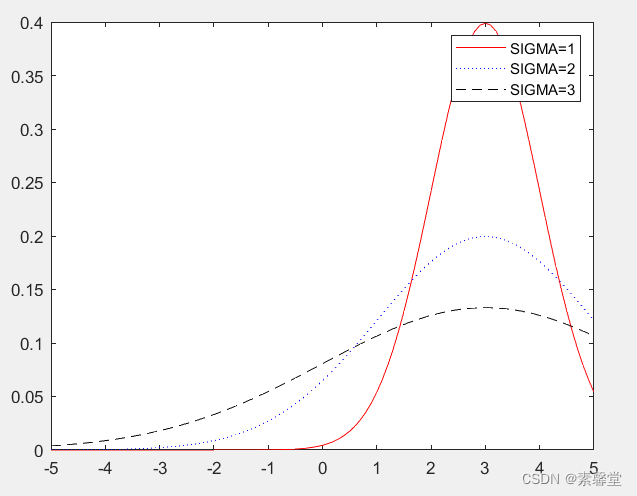
y3=normpdf(x1,3,1);         %SIGMA=1
y4=normpdf(x1,3,2);         %SIGMA=2
y5=normpdf(x1,3,3);         %SIGMA=3

 

figure;
plot(x1,y3,'r-',x1,y4,'b:',x1,y5,'k--');
legend('SIGMA=1','SIGMA=2','SIGMA=3');
y6=normpdf(x1,0,2);                   %MU=0
y7=normpdf(x1,2,2);                   %MU=2
y8=normpdf(x1,4,2);                   %MU=4

 

 

figure;
plot(x1,y6,'r-',x1,y7,'b:',x1,y8,'k--');
legend('MU=0','MU=2','MU=4');

 

%%  三大抽样分布的概率密度函数
%%  卡方分布
clear all;
x=0:0.1:15;
y1=chi2pdf(x,2);    %卡方分布n=2
y2=chi2pdf(x,3);    %卡方分布n=3
figure;
hold on;
plot(x,y1);
plot(x,y2,':');
legend('n=2','n=3');
title('卡方分布');

%%  t分布
clear all;
x=-5:0.1:5;
y1=tpdf(x,2);            %t分布（n=2）
y2=tpdf(x,10);           %t分布（n=10）  
figure;
plot(x,y1,'r:',x,y2,'b-');
legend('n=2','n=10');
title('t分布');

 

 

%% F分布
clear all;
x=0.1:0.1:5;
y=fpdf(x,2,5);             %F分布
figure;
plot(x,y,'r:');
title('F分布（m=2,n=5）');