考察点

第一次：2022年12月8日10:29:05

直接看代码的，在本子上写写画画

希望自己能够在第二次直接想到并写出中心扩散法 + 并且第二次就要了解清楚动态规划。

解题思路

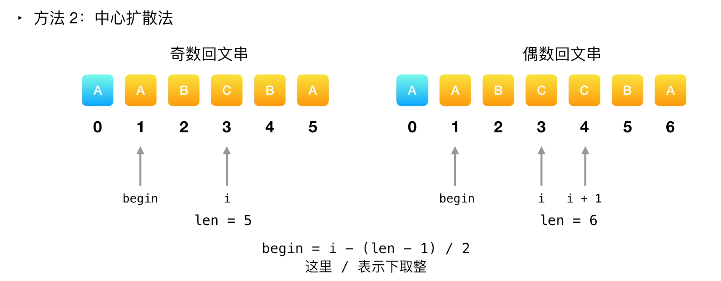
中心扩散法：确定一个中心，向两边扩散。
回文字符串：如果中心是一个回文字符串，扩散后满足：左边的字符跟右边的字符相等的话，那么这个扩散后的字符串一定是回文字符串。
回文字符串的中心，有可能是
- 示例 1 的情况，中心为1个字符
- 示例 2 的情况，中心为2个字符

根据中心的下标和长度，求回文字符串的开始位置：

在这里插入图片描述

代码展示：中心扩散

class Solution {
    public String longestPalindrome(String s) {

        if (s == null || s.length() < 1) {
            return "";
        }

        // 初始化最大回文子串的起点和终点
        int left = 0;
        int right = 0;

        for (int i = 0; i < s.length(); i++) {
            // 奇数回文中心的回文字符串长度
            int odd = palindromeLength(s, i, i);
            // 偶数回文中心的回文字符串长度
            int even = palindromeLength(s, i, i + 1);
            // 取最大值，对比奇数偶数的回文子串长度
            int maxLength = Math.max(odd, even);
            // TODO 计算对应最大回文子串的起点和终点
            if (maxLength > right - left) {
                left = i - (maxLength - 1) / 2;
                right = i + maxLength / 2;
            }
        }
        // 注意：这里的 end+1 是因为 java自带的左闭右开的原因
        return s.substring(left, right + 1);
    }

    private int palindromeLength(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            // 左边移动
            left--;
            // 右边移动
            right++;
        }
        /*
         * 需要推理计算：
         * 例如：caba的情况，跳出循环的时候，此时 ：start = 0 ; end = 4;
         * 肯定是 [(end - 1) - (start + 1 ) ] + 1 ，也就是 end - start - 1;
         */
        return right - left - 1;
    }
	
}

测试用例：

    public static void main(String[] args) {
        Solution solution = new Solution ();
        System.out.println(solution.longestPalindrome("babad"));
    }