前言

本专栏文章为本人AcWing算法基础课的学习笔记，课程地址在这。如有侵权，立即删除。

课前温习

番外：秦九韶算法

利用秦九韶算法来实现其他进制转十进制的结果求解

• 下图内容来源：百度百科，侵删。
  

核心模板

int nToTen(string s,int n){
	int ans=0;
	for(int i=0;i<s.size();i++){   
	   ans=ans*n+s[i]-'0';            
	}
	return ans;
}

主要代码

#include <iostream>
#include <string> 
using namespace std;
string s;
int n;
//其他进制转十进制（所有进制均适合） 
/*
int nToTen(string s,int n){
	int ans=0;
	for(int i=0;i<s.size();i++){
	if(s[i]>='A'&&s[i]<='Z') ans=ans*n+s[i]-'A'+10; 
	else ans=ans*n+s[i]-'0';
	}
	return ans;
} 
*/
//其他进制转十进制（仅能处理十进制以下的进制转十进制） 
int nToTen(string s,int n){
	int ans=0;
	for(int i=0;i<s.size();i++){   
	   ans=ans*n+s[i]-'0';            //可以这样理解：原始答案中一个数都没有，然后把第一个数加了进去，然后每次向答案中加数，都要将原来的答案整体向前移一位，空出位置留给当前位。所以结果就是ans往前移一位的结果再加上当前位的数字 
	}
	return ans;
} 
int main(){
    cin>>n;
    cin>>s;
    cout<<nToTen(s,n);
	return 0;
}

一、质数

（“就被称为质数”）

1. 试除法判定质数

小于x的约数是成对出现的（d和x/d），所以不需要从2枚举到n-1，只需要每次枚举较小的约数即可。即每次枚举从i到x/i。

核心模板

普通版

bool is_prime(int x){
    if(x<2) return false;
    for(int i=2;i<=x/i;i++){
        if(x%i==0){
            return false;
        }
    }
    return true;
}

优化版

bool is_prime(int x){
    if(x<=3) return x>1;
    if(x%6!=1&&x%6!=5) return false;
    for(int i=5;i<=x/i;i+=6){
        if(x%i==0&&x%(i+2)==0) return false;
    }
    return true;
}

题目链接：
866. 试除法判定质数

1.1题目描述

给定 n 个正整数 ai，判定每个数是否是质数。

输入格式

第一行包含整数 n。
接下来 n 行，每行包含一个正整数 ai。

输出格式

共 n 行，其中第 i 行输出第 i 个正整数 ai 是否为质数，是则输出 Yes，否则输出 No。

数据范围

1≤n≤100,1≤ai≤2³¹−1

输入样例：

2
2
6

输出样例：

Yes
No

1.2思路分析

套用模板即可，注意细节。

1.3代码实现

#include <iostream>
using namespace std;
const int N=110;
int a[N];
int n;
bool is_p(int n){
    if(n<2) return false;
    for(int i=2;i<=n/i;i++){
        if(n%i==0) return false;
    }
    return true;
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
        if(is_p(a[i]))  cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

2、试除法分解质因数

• 下图内容来源：百度百科，侵删。
  

思路：

• 下图内容来源这里，侵删。
  

核心模板

void divide(int x){
    for(int i=2;i<=x/i;i++){
        if(x%i==0){
            int s=0;
            while(x%i==0) x/=i,s++;
            cout<<i<<' '<<s<<endl;
        }
    }
    if(x>1) cout<<x<<' '<<1<<endl;
    cout<<endl;
}

题目链接：867. 分解质因数

1.4题目描述

给定 n 个正整数 ai ，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式

对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围

1≤n≤100,2≤ai≤2×10⁹

输入样例：

2
6
8

输出样例：

2 1
3 1

2 3

1.5思路分析

套用模板即可，注意细节。

1.6代码实现

#include <iostream>
using namespace std;
int n;
void divide(int n){
    for(int i=2;i<=n/i;i++){
        if(n%i==0){
            int s=0;
            while(n%i==0){
                n/=i;
                s++;
            }
            cout<<i<<' '<<s<<endl;
        }
    }
    if(n>1) cout<<n<<' '<<1<<endl;
    cout<<endl;
}
int main(){
    cin>>n;
    while(n--){
        int a;
        cin>>a;
        divide(a);
    }
    return 0;
}

二、筛素数

1.朴素筛法求素数

从2到n枚举每个数，删掉其所有的倍数，枚举完之后，没有被删掉的数为质数。

核心模板

int primes[N],cnt;   //primes[]存储所有素数
bool st[N];    //st[x]存储x是否被筛掉
void get_primes(int n){
    st[0]=st[1]=true;           //0和1均不是质数
    for(int i=2;i<=n;i++){
        if(st[i]) continue;
        primes[cnt++]=i;
        for(int j=i+i;j<=n;j+=i){
            st[j]=true;
        }
    }
}

埃氏筛法

int primes[N],cnt;   //primes[]存储所有素数
bool st[N];    //st[x]存储x是否被筛掉
void get_primes(int n){
    st[0]=st[1]=true;           //0和1均不是质数
    for(int i=2;i<=n;i++){
        if(!st[i]){
        primes[cnt++]=i;
        for(int j=i+i;j<=n;j+=i){
            st[j]=true;
        }
        }
    }
}

2.线性筛法求素数（O(n)）

核心模板

int primes[N],cnt;   //primes[]存储所有素数
bool st[N];   //st[x]存储x是否被筛掉
void get_primes(int n){
    st[0]=st[1]=true;           //0和1均不是质数
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){
            st[primes[j]*i]=true;
            if(i%primes[j]==0) break;
        }
    }
}

题目链接：868. 筛质数

2.1题目描述

给定一个正整数 n，请你求出 1∼n 中质数的个数。

输入格式

共一行，包含整数 n。

输出格式

共一行，包含一个整数，表示 1∼n 中质数的个数。

数据范围

1≤n≤10⁶

输入样例：

8

输出样例：

4

2.2思路分析

利用上述模板即可。

2.3代码实现

埃氏筛法

#include <iostream>
using namespace std;
const int N=1000010;
int n,cnt;
int primes[N];
bool st[N];
void getPrimes(int n){
     for(int i=2;i<=n;i++){
         if(!st[i]){
            primes[cnt++]=i;
            for(int j=i+i;j<=n;j+=i){
                st[j]=true;
            }
         }
     }
}
int main(){
    cin>>n;
    getPrimes(n);
    cout<<cnt;
    return 0;
}

线性筛法

#include <iostream>
using namespace std;
const int N=1000010;
int n,cnt;
int primes[N];
bool st[N];
void getPrimes(int n){
     for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){
            st[i*primes[j]]=true;
            if(i%primes[j]==0) break;    //此时primes[j]一定是i的最小质因子
        }
    }     
}
int main(){
    cin>>n;
    getPrimes(n);
    cout<<cnt;
    return 0;
}

三、欧几里得算法

核心思路：a与b的最大公约数等于b与a mod b的最大公约数。
最大公约数和最小公倍数的关系：

• 下图内容来源：百度百科，侵删。
  

核心模板

int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}

题目链接：872. 最大公约数

3.1题目描述

给定 n 对正整数 ai,bi，请你求出每对数的最大公约数。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个整数对 ai,bi。

输出格式

输出共 n 行，每行输出一个整数对的最大公约数。

数据范围

1≤n≤10⁵,1≤ai,bi≤2×10⁹

输入样例：

2
3 6
4 6

输出样例：

3
2

3.2思路分析

使用如上欧几里得算法。

3.3代码实现

#include <iostream>
using namespace std;
int n;
int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}
int main(){
    cin>>n;
    while(n--){
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
    }
    return 0;
}

四、快速幂

核心模板

求m^k mod p，时间复杂度O(logk)。

int qmi(int m,int k,int p){
    int res=1%p,t=m;
    while(k){
        if(k&1) res=res*t%p;
        t=t*t%p;
        k>>=1;
    }
    return res;
}

题目一

题目链接：875. 快速幂

4.1题目描述

给定 n 组 ai,bi,pi，对于每组数据，求出 ai^bi mod pi 的值。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含三个整数 ai,bi,pi。

输出格式

对于每组数据，输出一个结果，表示 ai^bi mod pi 的值。

每个结果占一行。

数据范围

1≤n≤100000,1≤ai,bi,pi≤2×10⁹

输入样例：

2
3 2 5
4 3 9

输出样例：

4
1

4.2思路分析

利用快速幂算法进行求解：首先预处理出a的次幂的结果，然后将a^k拆分成这些预处理结果的组合（将k拆成2的次方的和，即k的二进制表示为1的所有2的次幂），即利用这些预处理的结果来计算a^k。

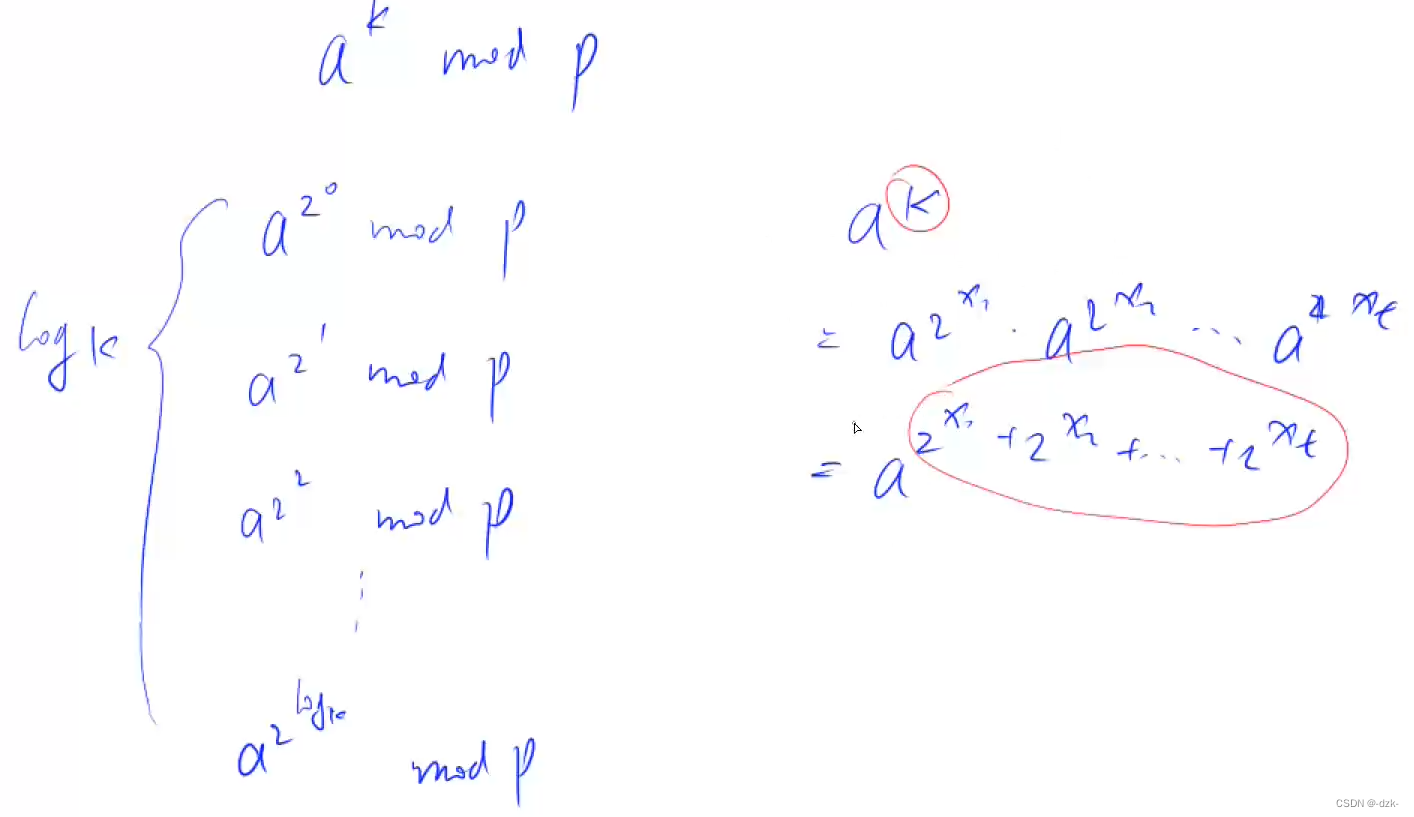
例子：

4.3代码实现

#include <iostream>
using namespace std;
typedef long long LL;
//快速幂，返回a^k%p的结果
int qmi(int a,int k,int p){
    LL res=1%p;         //存储结果
    while(k){         //枚举k的每位数字
        if(k&1) res=res*a%p;     //如果该位数字为1，则res乘上当前数字代表的二进制中的权重（即2的多少次幂）
        k>>=1;
        a=(LL)a*a%p;             //a每次翻倍，预处理出当前a的次幂的结果
    }
    return res;
}
int n;
int main(){
    cin>>n;
    while(n--){
        int a,k,p;
        cin>>a>>k>>p;
        cout<<qmi(a,k,p)<<endl;
    }
    return 0;
}

题目二

题目链接：876. 快速幂求逆元

4.4题目描述

给定 n 组 ai,pi，其中 pi 是质数，求 ai 模 pi 的乘法逆元，若逆元不存在则输出 impossible。

注意：请返回在 0∼p−1 之间的逆元。

乘法逆元的定义

若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a / ≡ a * x(mod m)，则称 x 为 b 的模 m 乘法逆元，记为 b⁻¹ (mod m)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，b^m−2 即为 b 的乘法逆元。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个数组 ai,pi，数据保证 pi 是质数。

输出格式

输出共 n 行，每组数据输出一个结果，每个结果占一行。

若 ai 模 pi的乘法逆元存在，则输出一个整数，表示逆元，否则输出 impossible。

数据范围

1≤n≤10⁵,1≤ai,pi≤2∗10⁹

输入样例：

3
4 3
8 5
6 3

输出样例：

1
2
impossible

4.5思路分析

由题目信息可得到以下化简。

该问题就化简成了求：b * x ≡ 1 (mod p )。x即为所求的逆元。
由费马小定理可知：b^p-1 ≡ 1 (mod p )。所以我们结合上述两个式子可知，x=b^p-2。

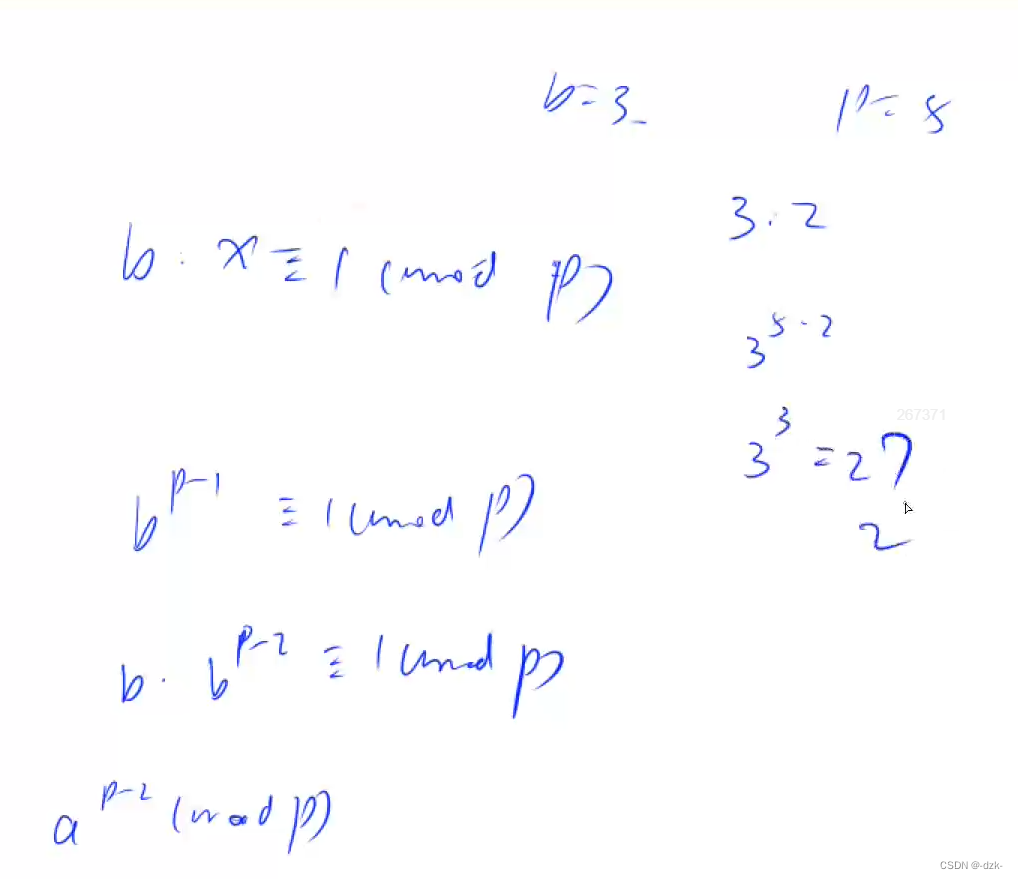
• 下图内容来源：百度百科，侵删。
  

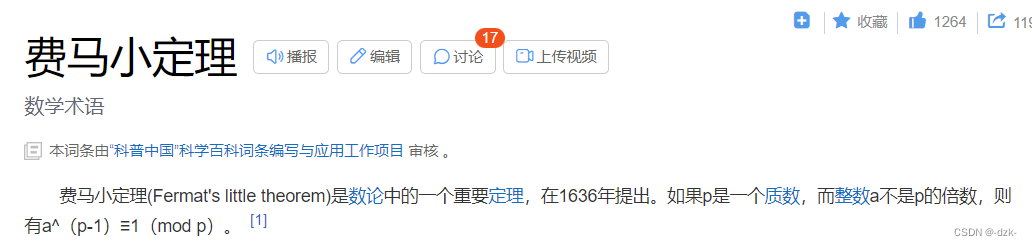
b如果是p的倍数则无解。
原因：如果p是b的倍数，那么p*x也是p的倍数，mod p之后一定等于0，不可能等于1（也就是得满足费马小定理的条件）。

4.6代码实现

#include <iostream>
using namespace std;
typedef long long LL;
//快速幂模板，返回a^k%p
int qmi(int a,int k,int p){
    LL res=1%p;
    while(k){
        if(k&1) res=res*a%p;
        k>>=1;
        a=(LL)a*a%p;
    }
    return res;
}
int n;
int main(){
    cin>>n;
    while(n--){
        int a,p;
        cin>>a>>p;
        int ans=qmi(a,p-2,p);      //ans代表所要求的逆元，即ans=a^p-2
        if(a%p) cout<<ans<<endl;   
        else cout<<"impossible"<<endl;    //无解情况：a%p=0时无解
    }
    return 0;
}

五、求组合数

核心模板

1. 根据下面公式来预处理出等式右边的组合数的值，那么等式左边就可以用等式右边已经算过的值来进行计算（有点像dp）。
   

//c[a][b]表示从a个苹果中选b个的方案数
for(int i=0;i<N;i++){
    for(int j=0;j<=i;j++){
        if(!j) c[i][j]=1;
        else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    }
}

2. 如下
   

首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]
如果取模的数是质数，可以用费马小定理求逆元
typedef long long LL;
//快速幂模版
int qmi(int a,int k,int p){
    LL res=1%p;
    while(k){
        if(k&1) res=res*a%p;
        k>>=1;
        a=(LL)a*a%p;
    }
    return res;
}
//预处理阶乘的余数和阶乘逆元的余数
fact[0]=infact[0]=1;
for(int i=1;i<N;i++){
    fact[i]=(LL)fact[i-1]*i%mod;
    infact[i]=(LL)infact[i-1]*qmi(i,mod - 2,mod)%mod;
}

题目一

题目链接：885. 求组合数 I

5.1题目描述

5.2思路分析

利用模板1求解即可。

5.3代码实现

#include <iostream>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N];
int n;
//求组合数
void solve(){
    for(int i=0;i<N;i++){
        for(int j=0;j<=i;j++){
            if(!j) c[i][j]=1;
            else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
        }
    }
}
int main(){
    cin>>n;
    solve();
    while(n--){
        int a,b;
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
    return 0;
}

题目二

题目链接：
886. 求组合数 II

5.4题目描述

5.5思路分析

利用模板2求解即可。

• 下图作者如图，侵删。
  

5.6代码实现

#include <iostream>
using namespace std;
typedef long long LL;
const int N=100010,mod=1e9+7;
int fact[N],infact[N];   //fact[i]存储i!%mod的值；infact[i]存储i!的逆元%mod的值
int n;
//快速幂模板
int qmi(int a,int k,int p){
    LL res=1%p;
    while(k){
        if(k&1) res=res*a%p;
        k>>=1;
        a=(LL)a*a%p;
    }
    return res;
}
int main(){
    cin>>n;
    fact[0]=infact[0]=1;    //0!%mod和其逆元%mod的值为1
    //预处理出fact[]和infact[]
    for(int i=1;i<N;i++){
        fact[i]=(LL)fact[i-1]*i%mod;            //求每个阶乘%mod的结果
        infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;    //求每个阶乘的逆元%mod的结果
    }
    while(n--){
        int a,b;
        cin>>a>>b;
        cout<<(LL)fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;    //按照组合数公式进行计算
    }
    return 0;
}

六、博弈论

NIM游戏

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。
我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理： NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ … ^ An != 0

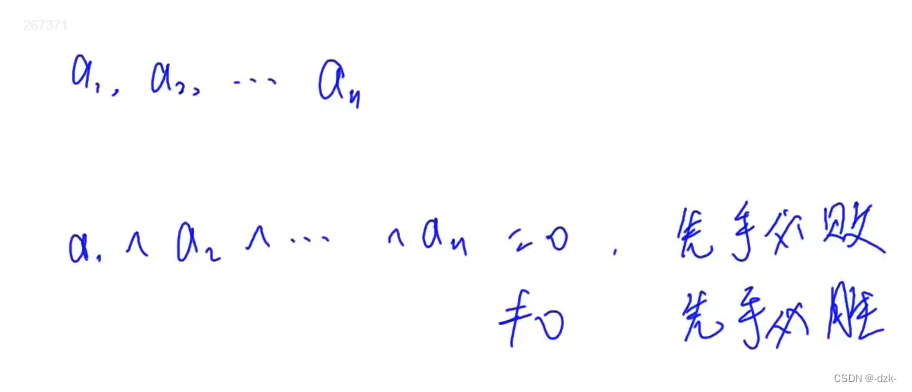
题目一

题目链接： 891. Nim游戏

6.1题目描述

给定 n 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 n。

第二行包含 n 个数字，其中第 i 个数字表示第 i 堆石子的数量。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

1≤n≤10⁵,1≤每堆石子数≤10⁹

输入样例：

2
2 3

输出样例：

Yes

6.2思路分析

计算所有数的异或值，如果值不为0，则先手必胜，否则先手必败。

6.3代码实现

#include <iostream>
using namespace std;
int n;
int main(){
    cin>>n;
    int res=0;
    while(n--){
        int x;
        cin>>x;
        res^=x;      //计算所有数的异或值
    }
    if(res) cout<<"Yes"<<endl;   //如果值不为0，则先手必胜
    else cout<<"No"<<endl;       //否则，先手必败
    return 0;
}

公平组合游戏ICG

若一个游戏满足：

1. 由两名玩家交替行动；
2. 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
3. 不能行动的玩家判负；

则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

Mex运算

设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：
mex(S) = min{x}, x属于自然数，且x不属于S。

SG函数

在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2, …, yk，定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果，即：
SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

有向图游戏的和

设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi，并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)

定理：
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

题目二

题目链接：893. 集合-Nim游戏

6.4题目描述

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S ，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 k，表示数字集合 S 中数字的个数。

第二行包含 k 个整数，其中第 i 个整数表示数字集合 S 中的第 i 个数 si。

第三行包含整数 n。

第四行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 hi。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

1≤n,k≤100,1≤si,hi≤10000

输入样例：

2
2 5
3
2 4 7

输出样例：

Yes

6.5思路分析

详见代码注释。

6.6代码实现

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;
const int N=110,M=10010;
int k,n;       //k为可以取石子的方案数（即一次取多少个）
int s[N],f[M];  //f[]存储每堆石子的sg值
//求石子数量为x的这一堆石子的sg值
int sg(int x){
    if(f[x]!=-1) return f[x];   //如果该值已经被算过则直接返回
    unordered_set<int> S;     //存放x各个后继结点的sg值
    //遍历k种取法
    for(int i=0;i<k;i++){
        int sum=s[i];          //sum为本次取法取多少个石子
        if(x>=sum) S.insert(sg(x-sum));    //如果可以取，则将取后的后继结点的sg值加入S
    }
    for(int i=0;;i++){
        //对S求mex，求出不在集合中的最小自然数
        if(!S.count(i)) return f[x]=i;
    }
}
int main(){
    cin>>k;
    for(int i=0;i<k;i++) cin>>s[i];
    cin>>n;
    int ans=0;
    memset(f,-1,sizeof f);
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        ans^=sg(x);    //n堆石子的sg的值异或起来不为0，则先手必胜
    }
    if(ans) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
    return 0;
}

七、约数个数和约数之和

• 下图作者如图，侵删。
  
• int范围内的数最多约数个数约为1600个
  

核心模板

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

题目链接：
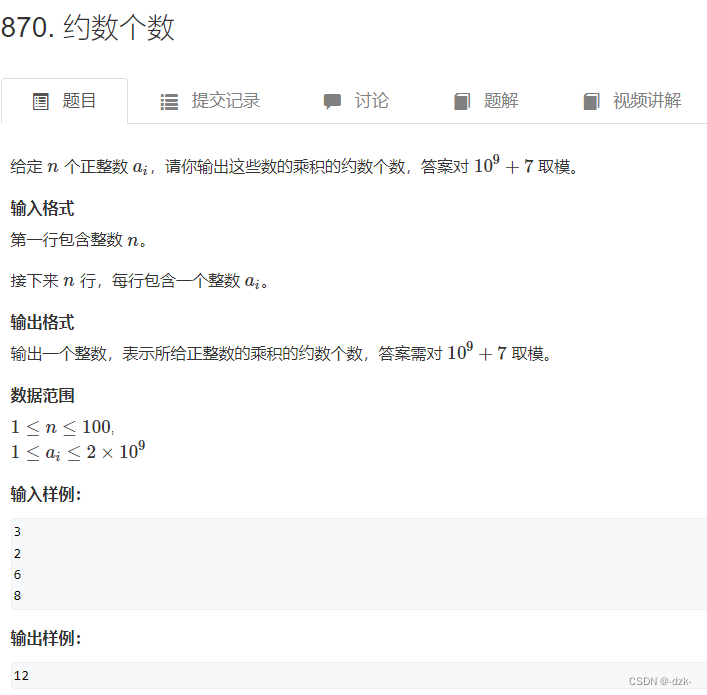
870. 约数个数

7.1题目描述

7.2思路分析

将每个数质因数分解，利用unordered_map进行存储所有pi及其指数，即每分解一个数，将分解后对应的pi的指数加上分解质因数的次数。

7.3代码实现

#include <iostream>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
int n;
int main(){
    cin>>n;
    unordered_map<int,int> hash;   //存储每个pi和其指数
    while(n--){
        int a;
        cin>>a;
        for(int i=2;i<=a/i;i++){   //注意循环从2~a/i
            while(a%i==0){
                hash[i]++;   //i的指数++
                a/=i;  
            }
        }
        if(a>1) hash[a]++;    //注意if位置
    }
    LL ans=1;
    for(auto i:hash) ans=ans*(i.second+1)%mod;
    cout<<ans;
    return 0;
}