62.不同路径（注意初始化）

• 本题初始化很重要，初始化的同时还要考虑越界的问题与可能性。
• 这道题需要和不同路径Ⅱ对比来看，就能看出初始化重要性，同时这两道题补充了一些关于for循环终止条件和执行的问题。

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10^9

BFS深度搜索写法

本题因为是给出了图寻找路径，最直观的想法就是用图论里的深搜，来枚举出来有多少种路径。

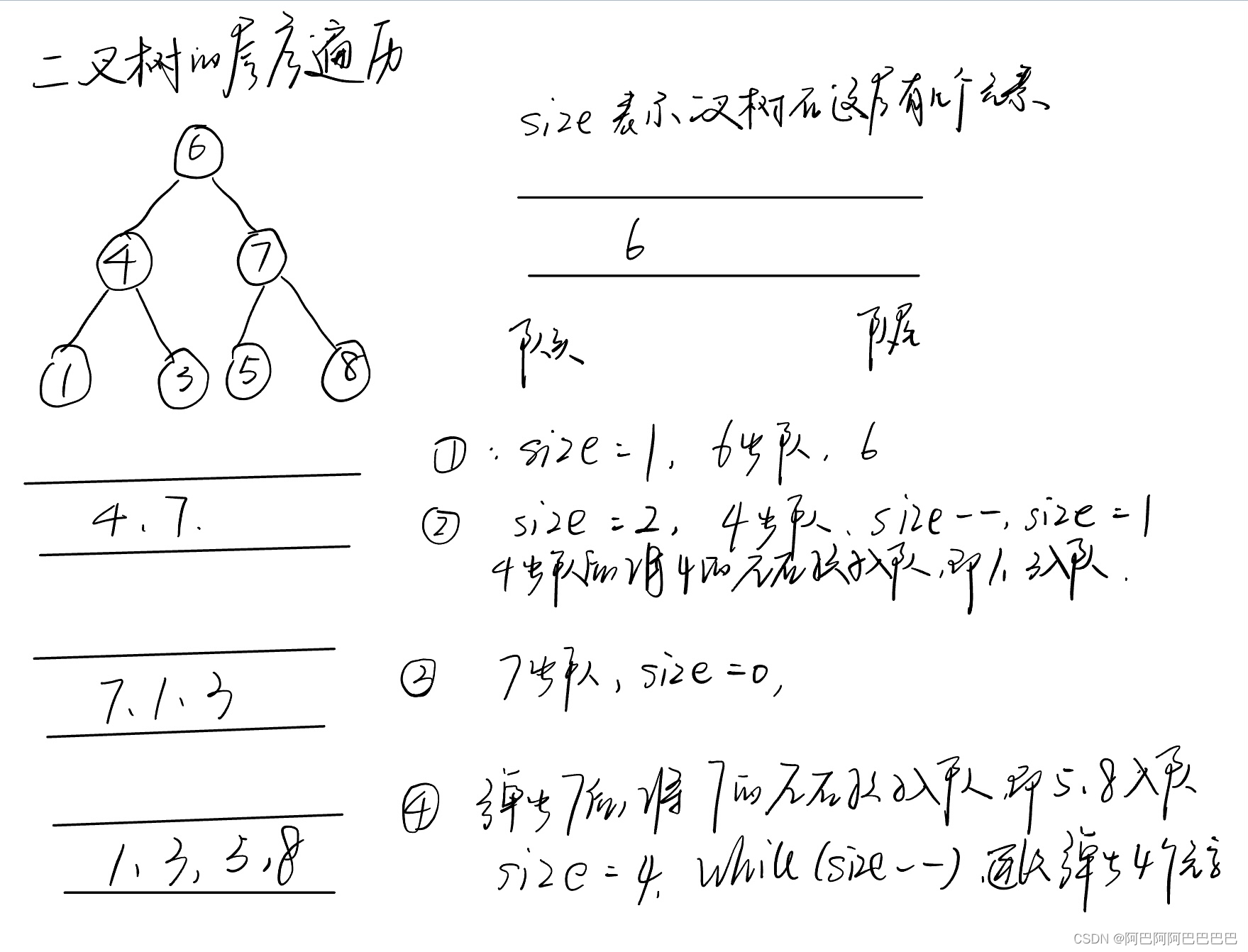
注意题目中说机器人每次只能向下或者向右移动一步，那么其实机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

例如下图所示的例子：

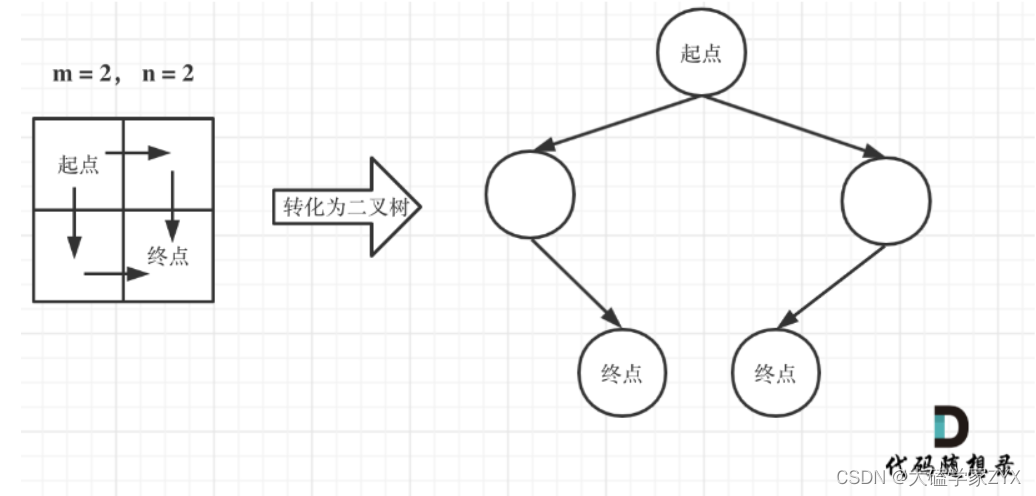
此时问题就可以转化为求二叉树叶子节点的个数，代码如下：

class Solution {
private:
    int dfs(int i, int j, int m, int n) {
        if (i > m || j > n) return 0; // 越界了
        if (i == m && j == n) return 1; // 找到一种方法，相当于找到了叶子节点
        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
    }
public:
    int uniquePaths(int m, int n) {
        return dfs(1, 1, m, n);
    }
};

但是这么写，提交了代码会发现超时！

实际上是因为这个深搜的算法，其实就是要遍历整个二叉树。

这棵树的深度是m+n-1（深度按从1开始计算），那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树（其实没有遍历整个满二叉树，只是近似而已）

所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1)，可以看出，这是指数级别的时间复杂度，是非常大的。

再复习一下数据范围和时间复杂度的关系，可以看出，指数级别的时间复杂度是需要n<=30才行的。

动态规划思路

DP需要记录每一个格子的状态，这样才能用状态转移方程进行格子状态的转换.

因为本题需要记录格子状态，因此我们需要定义一个二维的dp数组。

DP数组的含义

二维数组dp[i][j]的含义应该是，从[0,0]位置到[i,j]位置，有多少条不同的路径。因为待求的量就是路径数目。

递推公式

因为题目描述中说，机器人只能往下走或者往右走一步，因此，对于一个位置[i,j]，他的上一个位置到达当前位置的路径最多只有两条，就是从上面来和从左边来。如下图所示。

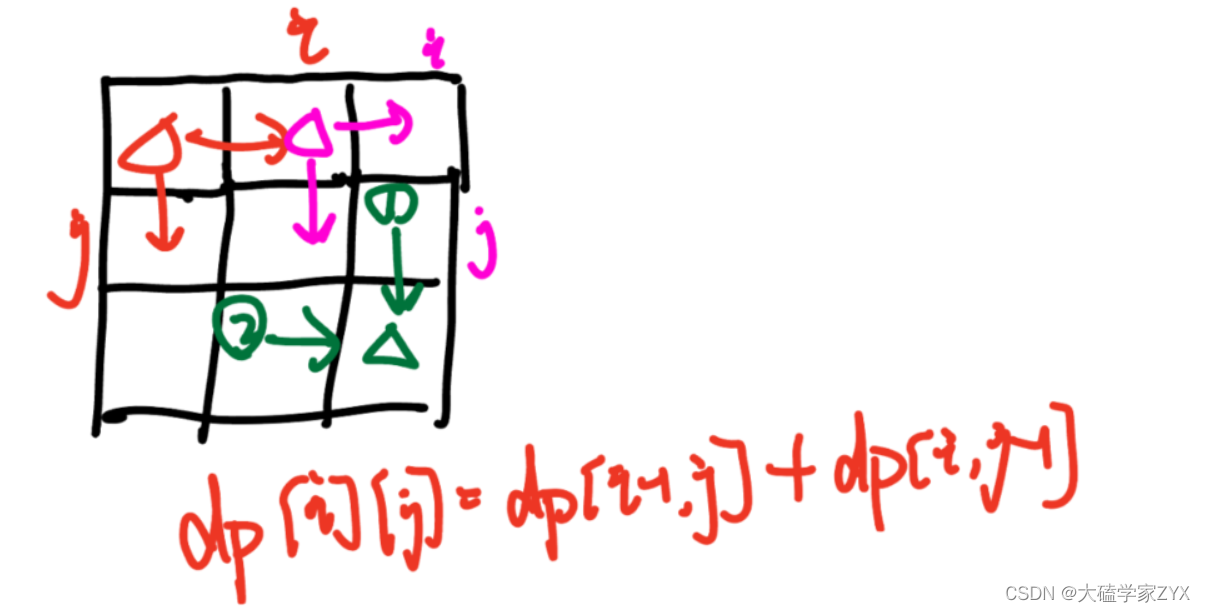
因此递推公式为：dp[i][j] = dp[i-1][j]+dp[i,j-1]

DP数组初始化

机器人从左上角的[0,0]开始走，由于数组下标越界影响，i和j都需要从1开始，也就是说，只要是i=0,j=0的情况，就会出现-1的下标越界，因此dp[i][0]和dp[0][j]这两行都需要做初始化！

初始化逻辑：

dp[i][0]就是一路横着走过去，路径数目就是1（因为只有这一个方向，也就是只有一条路径，注意这里是统计路径条数而不是走了几步），dp[0][j]同理

//直接从0开始初始化就行，初始化的时候不需要在意边界条件，[0][0]不存在越界问题
//j是0,横着只有一条路径方向
for(int i=0;i<m;i++){
    dp[i][0]=1;
}
//i是0，竖着也只有一条路径方向
for(int j=0;j<n;j++){
    dp[0][j]=1;
}

遍历顺序

递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

打印dp数组

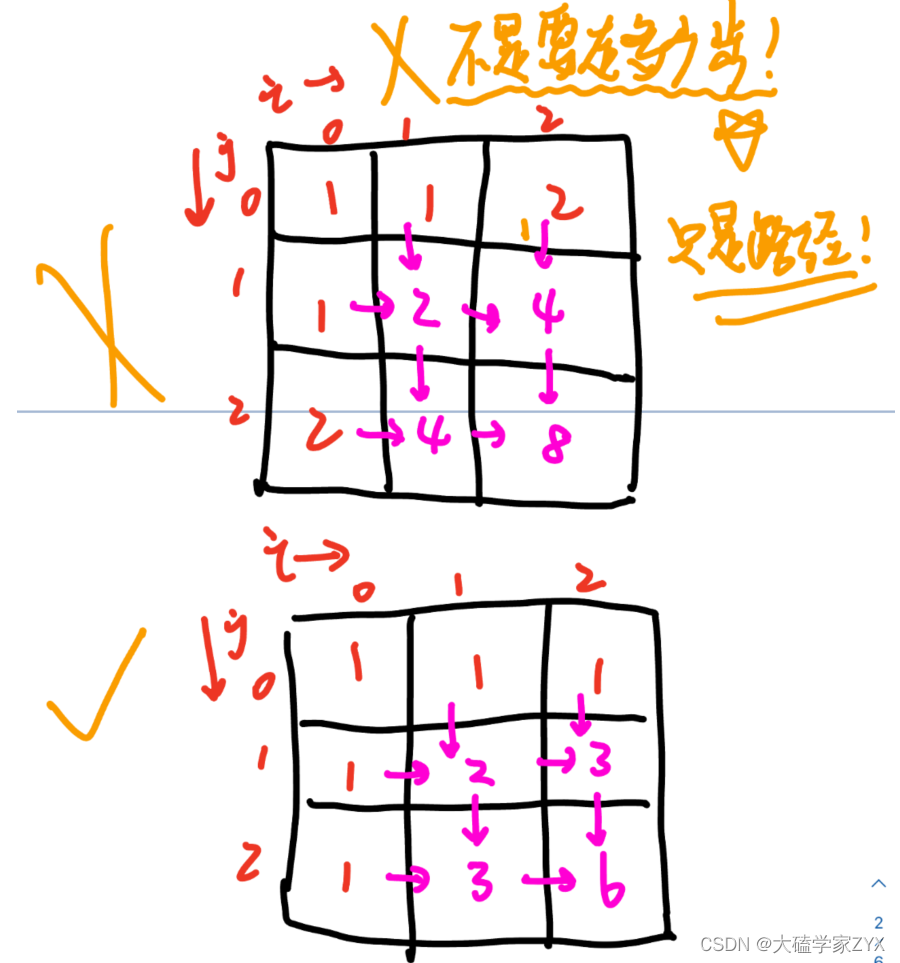
DP数组预期例子如图：

（这里一定要区分走多少步和路径的区别，路径的初始化是同个方向全部为1，但是走多少步的初始化是同个方向为i的递增）

正确的DP数组预期如下图第二个所示。

动态规划写法

• 二维数组初始化的方式：先放一维数组个数，再初始化内部的一维数组，如vector<vector<int>>dp(m,vector<int>(n,0))(得到m*n，初值全部为0的二维矩阵)

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m==0&&n==0) return 0;
        //二维数组初始化的方式：先放一维数组个数，再初始化内部的一维数组
        vector<vector<int>>dp(m,vector<int>(n,0));
        //dp数组初始化
        for(int i=0;i<m;i++){
            dp[i][0]=1;
        }
        for(int j=0;j<n;j++){
            dp[0][j]=1;
        }
        //递推公式
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];

    }
};

• 时间复杂度：O(m × n)
• 空间复杂度：O(m × n)

数组越界的问题

本题提示里面1 <= m, n <= 100，也就是说m n都是正整数。加上本题递推公式只涉及到了i-1，因此>=1的情况都不会越界。

并且本题是网格前提，m和n要么全部=0，要么都不为0，不存在m和n其中一个是0的情况。

即使存在 m 或 n 为 0， for 循环也不会执行，因为它们是从 0 到 m 或 n 的，所以在这个情况下代码是安全的。

for循环执行的问题

下列初始化的代码，在m=0，n=0的时候，for循环是不会执行的。因为在 C++ 中，for 循环的条件是在每次循环开始之前检查的。

假设 m 是 0，那么 for(int i=0; i<m; i++) 就会立即结束，因为条件 i<m 在一开始就不满足（0不小于0）。

同理，如果 n 是 0，那么 for(int j=0; j<n; j++) 也会立即结束，因为条件 j<n 在一开始就不满足。

//dp数组初始化
for(int i=0;i<m;i++){
   dp[i][0]=1;
}
for(int j=0;j<n;j++){
   dp[0][j]=1;
}

因此，即使m和n是0，也不会执行for循环的代码，同样也不会执行递推公式的for循环，因为一开始就不满足i<m的条件。

63.不同路径Ⅱ（初始化区别）

• 本题和上一题最大区别就在于初始化，本题的初始化需要考虑到，初始化i=0的时候，障碍物的存在会导致后面的全部被堵死，这种情况需要直接break，而不是只置零
• 而遍历到内部的时候，由于递推公式执行之前先判断是否是障碍物，因此障碍物直接置零，还有其他的路径可以相加，所以continue

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

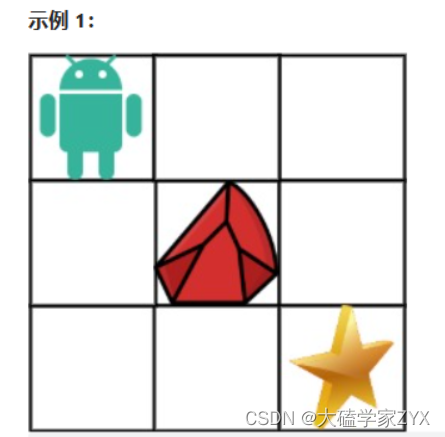
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

思路

本题相对于上一题不同路径，实际上只是加上了障碍。本题加上了输入的数组，输入数组里数值为1的，就是有障碍的情况。

本题和上一道题目的基本思路都是相同的，但是我们需要把二维数组中的1变量的dp值全部置零，就可以消除掉障碍物的路径。

DP数组含义

本题DP数组仍然是表示当前累积的路径总数。

递推公式

dp[i][j]=dp[i-1][j]+dp[i][j-1]，当有障碍物的时候，赋值dp[i][j]=0

DP数组初始化

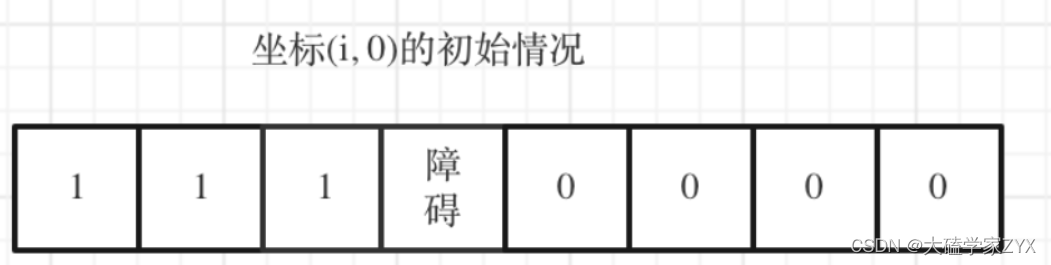
在上一道题目中，最开始i=0的一整行，和j=0的一整列，都要初始化成1，因为递推公式里面的i-1和j-1存在下标越界的问题。

但是本题中，我们处理第一行和第一列的时候，一旦有障碍，for循环需要立即break。因为本题只能往右边和下边移动，因此只要有障碍，最上面的第一行后面的路径就全部作废了。

但是在二维矩阵内部，如果有障碍可以直接选择continue，因为下一个累加的时候，初始值0不会给累加做贡献。

最开始的写法：初始化有问题

• 注意二维数组获得m和n的方法，m直接=r.size()，n=r[0].size()

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();//得到二维数组一边
        int n=obstacleGrid[0].size();//二维数组另一边
        //cout<<m<<" "<<n<<endl;
        if(m==0&&n==0) return 0;
        //特殊情况：如果起点or终点是1 直接返回
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0
            return 0;
        vector<vector<int>>dp(m,vector<int>(n,0));//建立相同大小，初始值全是0的DP数组
        //初始化
        for(int i=1;i<m;i++){
            if(obstacleGrid[i][0]==1){
                dp[i][0]=0;
            }
            else{
                dp[i][0]=1;
            }
        }
        for(int j=1;j<n;j++){
            if(obstacleGrid[0][j]==1){
                dp[0][j]=0;
            }
            else{
                dp[0][j]=1;
            }
        }
        //打印DP结果调试
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                cout<<dp[i][j]<<" ";
            }
             cout<<endl;   
        }
        //递推公式
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]!=1){
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
                else{
                    dp[i][j]=0;
                }
                //cout<<dp[i][j]<<" ";
            }
        }
        return dp[m-1][n-1];
    }
};

这里的问题在于初始化。

修改完整版

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        //如果起点或者终点障碍，直接返回0
        if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) return 0;
        //创建dp数组 m*n矩阵
        vector<vector<int>>dp(m,vector<int>(n,0));
        //dp数组初始化
        for(int i=0;i<m;i++){
            if(obstacleGrid[i][0]==1) break; //如果是障碍物，那么这一行后面都无效，因为只能向右边和下边走
            else
                dp[i][0]=1; 
        }
        for(int j=0;j<n;j++){
            if(obstacleGrid[0][j]==1) break;
            else
                dp[0][j]=1;
        }
        //递推公式
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]==1) continue;
                else{
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

for循环遍历条件的问题

本题的初始化代码还可以写成：

vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

与下面这段代码是等价的。

for (int i = 0; i < m ; i++) {
    if(obstacleGrid[i][0] == 1) break;
    dp[i][0] = 1;
}
for (int j = 0; j < n ; j++) {
    if(obstacleGrid[0][j] == 1) break;
    dp[0][j] = 1;
} 

这是因为for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作。

在C++中，for循环的格式是for (initialization; condition; increment)。当条件condition为假时，for循环将立即停止，不再执行后面的步骤，这与break语句的作用是一样的。

第一种写法的条件部分是 i < m && obstacleGrid[i][0] == 0。当 i < m 是真的，但 obstacleGrid[i][0] == 0 是假的时，这个条件就会是假的，因此for循环会停止。

第二种写法使用了break语句来实现同样的效果。当 obstacleGrid[i][0] == 1 是真的时，break语句会被执行，这导致for循环立即停止，不再执行后面的步骤。

所以说，这是for循环的特性，即它的条件部分可以被看作是每次循环都要检查的一个断言，只有当这个断言是真的时，循环才会继续。当断言变为假时，循环立即终止。这和break语句效果相同。

总结

就算是做过62.不同路径，在做本题也会有感觉遇到障碍无从下手。

其实只要考虑到，遇到障碍dp[i][j]保持0就可以了。

也有一些重要的初始化细节，例如：初始化的部分，很容易忽略了障碍之后应该都是0的情况。