Ceres是由Google开发的开源C++通用非线性优化库,与g2o并列为目前视觉SLAM中应用最广泛的优化算法库。
对于任何一个优化问题,我们首先需要对问题进行建模,之后采用合适的优化方法,进行求解。在求解的过程中,往往需要进行梯度下降求取最优,这里涉及了导数计算。所以在代码中使用Ceres进行优化时,需要包含基本内容:建模、优化、求导方法。
Ceres库简介
Ceres库主要用于求解无约束或者有界约束的最小二乘问题。其数学形式如下:
min x 1 2 ∑ i ρ i ( ∥ f i ( x 1 , ⋯ , x k ) ∥ 2 ) s.t. l j ≤ x j ≤ u j \begin{split} \min_{\boldsymbol{x}} &\quad \frac{1}{2}\sum_{i} \rho_i\left(\left\|f_i\left(x_1, \cdots ,x_k\right)\right\|^2\right) \\ \text{s.t.} &\quad l_j \le x_j \le u_j \end{split} xmins.t.21i∑ρi(∥fi(x1,⋯,xk)∥2)lj≤xj≤uj
我们的任务就是找到一组满足约束 l j ≤ x j ≤ u j l_j \le x_j \le u_j lj≤xj≤uj的 x 1 , ⋯ , x k x_1, \cdots, x_k x1,⋯,xk,使得优化目标函数
1 2 ∑ i ρ i ( ∥ f i ( x 1 , ⋯ , x k ) ∥ 2 ) \begin{split}\frac{1}{2}\sum_{i} \rho_i\left(\left\|f_i\left(x_1, \cdots ,x_k\right)\right\|^2\right)\end{split} 21i∑ρi(∥fi(x1,⋯,xk)∥2)
取值最小。
其中的一些变量的解释:
- 优化参数
x
1
,
⋯
,
x
k
x_1, \cdots, x_k
x1,⋯,xk:
参数块(ParameterBlock),它们的取值就是我们要寻找的解 - l j , u j l_j, u_j lj,uj:第 j j j个优化参数 x j x_j xj的下界和上界
- 表达式
ρ
i
(
∥
f
i
(
x
1
,
⋯
,
x
k
)
∥
2
)
\rho_i\left(\left\|f_i\left(x_1, \cdots ,x_k\right)\right\|^2\right)
ρi(∥fi(x1,⋯,xk)∥2):
残差块(ResidualBlock) -
f
i
(
⋅
)
f_i(\cdot)
fi(⋅):
代价函数(CostFunction) -
ρ
i
(
⋅
)
\rho_i(\cdot)
ρi(⋅):
损失函数,或者核函数(LossFunction)。它的意义主要是为了降低野点(outliers)对于解的影响
代价函数同时负责计算残差项( f i ( x 1 , ⋯ , x k ) f_i\left(x_1, \cdots ,x_k\right) fi(x1,⋯,xk))和雅可比矩阵( J i \mathcal{J}_i Ji)。
J i = ∂ ∂ x i f i ( x 1 , ⋯ , x k ) ∀ i ∈ 1 , ⋯ , k \mathcal{J}_i = \frac{\partial}{\partial x_i} f_i\left(x_1, \cdots ,x_k\right) \qquad \forall i \in {1,\cdots,k} Ji=∂xi∂fi(x1,⋯,xk)∀i∈1,⋯,k
很多时候我们说最小二乘都是拿来做曲线拟合的,实际上只要能够把问题描述成上面的数学形式,就都可以使用Ceres来求解。使用起来也比较简单,只要按照教程介绍的套路,提供代价函数的计算方式,描述清楚每个残差块以及核函数即可。
如下面的示例代码所示,一般我们需要定义三个对象,problem用于描述将要求解的问题,options提供了很多配置项,而summary用于记录求解过程。
ceres::Problem problem;
ceres::Solver::Options options;
ceres::Solver::Summary summary;
Ceres的求解过程包括构建最小二乘和求解最小二乘问题两部分,其中构建最小二乘问题的相关方法均包含在Ceres::Problem类中,涉及的成员函数主要包括Problem::AddResidualBlock()和Problem::AddParameterBlock()。
注意:Ceres Solver只接受最小二乘优化,也就是 min r T r \min r^{T} r minrTr;若要对残差加权重,使用马氏距离,即 min r T P − 1 r \min r^{T} P^{-1} r minrTP−1r,则要对信息矩阵 P − 1 P^{-1} P−1做Cholesky分解,即 L L T = P − 1 L L^{T} = P^{-1} LLT=P−1,则 d = r T ( L L T ) r = ( L T r ) T ( L T r ) d = r^{T} (L L^{T}) r = (L^T r)^T (L^T r) d=rT(LLT)r=(LTr)T(LTr) ,令 r ′ = L T r r^{'} = L^T r r′=LTr ,最终 min r ′ T r ′ \min r^{'T} r^{'} minr′Tr′。
ceres使用流程

使用 Ceres Solver 求解非线性优化问题,主要包括以下几部分:
-
【STEP 1】构建优化问题(ceres::Problem)
-
【STEP 2】构建代价函数(ceres::CostFunction)或残差(residual)
-
【STEP 3】添加代价函数、核函数:通过ceres::Problem::AddResidualBlock添加代价函数(cost function)、核函数(loss function)和输入参数块(即待优化状态量块)
-
【STEP 4】配置求解器(ceres::Solver::Options)
-
【STEP 5】运行求解器(ceres::Solve(options, &problem, &summary))
下面将会对其中的重要的几个STEP进行详细讲解。
构建代价函数(STEP2)

代价函数最重要的功能就是计算残差向量和雅可比矩阵。Ceres提供了三种求导方法,分别是:解析求导、自动求导、数值求导。
在SLAM中,使用的一般都是解析求导,这种方法需要自己填入雅克比函数。
基础代价函数类
先看下最基础的代价函数类的声明:
class CostFunction {
public:
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const = 0;
const vector<int32>& parameter_block_sizes();
int num_residuals() const;
protected:
vector<int32>* mutable_parameter_block_sizes();
void set_num_residuals(int num_residuals);
};
CostFunction的输入参数块的数量和大小以及输出的数量,分别存储在CostFunctio::parameter_block_sizes_和CostFunction::num_residuals_中。从此类继承的子类应使用对应的访问器设置这两个成员。当使用Problem::AddResidualBlock()添加代价函数时,此信息将由Problem验证。
CostFunction中有一个纯虚函数需要子类进行重写,该纯虚函数的定义为:
bool CostFunction::Evaluate(double const *const *parameters,
double *residuals,
double **jacobians) const;
纯虚函数的形参的解释:
- parameters:输入参数块,大小为parameter_block_sizes_.size()的数组(输入参数块的数量),parameters[i]是大小为parameter_block_sizes_[i]的数组(第i个输入参数块的维度)
- residuals:残差,大小为num_residuals_的数组
- jacobians:雅可比矩阵,大小为parameter_block_sizes_.size()的数组的数组(输入参数块的数量),jacobians[i]是大小为num_residuals乘parameter_block_sizes_[i]的行优先数组(残差对第i个输入参数块求导,即大小为残差维度 乘 第i个输入参数块维度,再转化为行优先数据组)
jacobians的详细表达式为:
jacobians[i][r * parameter_block_sizes_[i] + c] = ∂ residual [ r ] ∂ parameters [ i ] [ c ] \text{jacobians[i][r * parameter\_block\_sizes\_[i] + c]}=\frac{\displaystyle \partial \text{residual}[r]}{\displaystyle \partial \text{parameters}[i][c]} jacobians[i][r * parameter_block_sizes_[i] + c]=∂parameters[i][c]∂residual[r]
parameters和residuals不能为nullptr,jacobians可能为nullptr。如果jacobians为nullptr,则用户只需计算残差即可。
纯虚函数的返回值指示残差或雅可比的计算是否成功。
如果输入参数块的大小和残差向量的大小在编译时已知(这是常见情况),则可以使用SizedCostFunction。这些已知值可以指定为模板参数,并且用户只需要实现CostFunction::Evaluate()。
template<int kNumResiduals, int... Ns>
class SizedCostFunction : public CostFunction {
public:
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const = 0;
};
该模板参数的含义为:
- kNumResiduals:残差的维度,即num_residuals_的值
- Ns:不定参数的数量为输入参数块的数量,即parameter_block_sizes_.size(),每个不定参数对应的值为每个输入参数块的维度,即parameter_block_sizes_[i]的值
Ceres提供的三种求导方法,都是基于上面的基础代价函数类实现的。
解析求导
解析求导(Analytic Derivatives),也被称为自定义求导。解析求导需要自行定义迭代求导时的雅克比矩阵和残差。需要以下几个步骤:
- 构建一个继承自ceres::SizedCostFunction的类,同样,对于模板参数的数字,第一个为残差的维度,后面几个为输入参数块的维度
- 重载纯虚函数Evaluate(…),根据输入参数块,实现残差和雅克比矩阵的计算
在ceres中的代价函数里面Evaluate()采用的是纯虚函数:
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const = 0;
下面以最小二乘 min x 1 2 ( 10 − x ) 2 \underset{x}{\min} \frac{1}{2}(10-x)^{2} xmin21(10−x)2为例解析求导。显然残差为 ( 10 − x ) (10−x) (10−x),而雅可比矩阵维度为 1 ∗ 1 1∗1 1∗1且为常数 − 1 -1 −1。在求导的Evaluate()函数中定义残差和雅克比如下:
class SimpleCostFunction : public ceres::SizedCostFunction<1, 1> {
public:
virtual ~SimpleCostFunction() {};
// 形参: 输入参数块, 残差, 雅可比矩阵
virtual bool Evaluate(double const* const* parameters, double *residuals,
double** jacobians) const {
const double x = parameters[0][0];
residuals[0] = 10 - x;
if (jacobians != NULL && jacobians[0] != NULL) {
jacobians[0][0] = -1;
}
return true;
}
};
ceres::CostFunction* cost_function = new SimpleCostFunction();
下面以最小二乘 min x 1 2 ( k − x T y ) 2 \underset{x}{\min} \frac{1}{2}(k-x^Ty)^{2} xmin21(k−xTy)2为例解析求导,其中 x x x、 y y y为二维向量变量, k k k为常数。显然残差为 k − x T y k-x^Ty k−xTy:
class SimpleCostFunction : public ceres::SizedCostFunction<1, 2, 2> {
public:
virtual ~SimpleCostFunction(double k) : k_(k) {};
// 形参: 输入参数块, 残差, 雅可比矩阵
virtual bool Evaluate(double const* const* parameters, double *residuals,
double** jacobians) const {
const double x0 = parameters[0][0];
const double x1 = parameters[0][1];
const double y0 = parameters[1][0];
const double y1 = parameters[1][1];
residuals[0] = k_ - x0 * y0 - x1 * y1;
if (jacobians != NULL && jacobians[0] != NULL) {
jacobians[0][0] = -y0;
jacobians[0][1] = -y1;
jacobians[1][0] = -x0;
jacobians[1][1] = -x1;
}
return true;
}
private:
double k_;
};
ceres::CostFunction* cost_function = new SimpleCostFunction();
对于,ceres::SizedCostFunction<x, y, z, …>的几个模板参数与Evaluate函数的形参对应关系:
-
x x x决定了residuals的维度
-
y , z , . . . y, z, ... y,z,...的个数决定了输入参数块的个数,即parameters的第一维度,而 y y y、 z z z本身的值决定了每个输入参数块的维度,即parameters的第二维度
-
y , z , . . . y, z, ... y,z,...的个数决定了输入参数块的个数,即jacobians的第一维度,而 x x x的值(行数)和 y y y、 z z z本身的值(列数)的乘积决定了每个输入参数块的雅可比矩阵的维度,即jacobians的第二维度(按行优先的顺序排列)
自动求导
自动求导(Automatic Derivatives)是Ceres很神奇的一个功能,它能够对于一些数据形式较为基础的表达式,自动求解出导数形式。采用的原理是对偶数(dual numbers)和Jets格式实现的,不理解具体细节也不影响使用。
如果想要了解自动求导的原理,可以参考文章:Ceres的数值求导与自动求导的原理。
自动求导的代价函数类定义为AutoDiffCostFunction类,其函数声明为:
template <typename CostFunctor,
int kNumResiduals, // Number of residuals, or ceres::DYNAMIC.
int... Ns> // Size of each parameter block
class AutoDiffCostFunction : public
SizedCostFunction<kNumResiduals, Ns> {
public:
AutoDiffCostFunction(CostFunctor* functor, ownership = TAKE_OWNERSHIP);
// Ignore the template parameter kNumResiduals and use
// num_residuals instead.
AutoDiffCostFunction(CostFunctor* functor,
int num_residuals,
ownership = TAKE_OWNERSHIP);
};
想要使用自动求导,就必须构造代价函数结构体CostFunctor(采用类模板形式),并在其结构体内对模板括号运算符() 重载,定义残差。在重载的()运算符形参中,最后一个为残差(唯一的非常量形参),前面几个为输入参数块。函数返回true表示成功。
注意:采用自动求导时,即使是整数也要写成浮点型,否则会报错Jet类型匹配错误。
下面以最小二乘 min x 1 2 ( 10 − x ) 2 \underset{x}{\min} \frac{1}{2}(10-x)^{2} xmin21(10−x)2为例自动求导。显然残差为 ( 10 − x ) (10−x) (10−x):
struct CostFunctor {
// 形参: 输入参数块, 残差
template<typename T>
bool operator()(const T *const x, T *residual) const {
residual[0] = 10.0 - x[0];
return true;
}
};
// 模板参数: 代价函数结构体, 残差维度, 输入参数块维度
ceres::CostFunction *cost_function
= new ceres::AutoDiffCostFunction<CostFunctor, 1, 1>(
new CostFunctor());
下面以最小二乘 min x 1 2 ( k − x T y ) 2 \underset{x}{\min} \frac{1}{2}(k-x^Ty)^{2} xmin21(k−xTy)2为例自动求导,其中 x x x、 y y y为二维向量变量, k k k为常数。显然残差为 k − x T y k-x^Ty k−xTy:
class CostFunctor {
CostFunctor(double k): k_(k) {}
// 形参: 输入参数块, 残差
template <typename T>
bool operator()(const T* const x , const T* const y, T* e) const {
e[0] = k_ - x[0] * y[0] - x[1] * y[1];
return true;
}
private:
double k_;
};
// 模板参数: 代价函数结构体, 残差维度, 输入参数块维度
ceres::CostFunction* cost_function
= new ceres::AutoDiffCostFunction<CostFunctor, 1, 2, 2>(
new CostFunctor(1.0)); ^ ^ ^
| | |
Dimension of residual ------+ | |
Dimension of x ----------------+ |
Dimension of y -------------------+
对于,ceres::AutoDiffCostFunction<CostFunctor, x, y, z, …>的几个模板参数与CostFunctor的模板括号运算符()的形参对应关系:
-
x x x决定了residuals的维度
-
y , z , . . . y, z, ... y,z,...的个数决定了输入参数块的个数,即模板括号运算符
()的常量形参(除最后一个形参)个数,而 y y y、 z z z本身的值决定了每个输入参数块的维度,即每个常量形参的维度 -
x x x决定了模板括号运算符
()的非常量形参(最后一个形参)的维度
数值求导
数值求导(Numeric derivatives)核心思想是,当增量很小时,可以采用
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
\underset{\Delta x \to 0}{\lim} \frac{f(x+\Delta x)-f(x)}{\Delta x}
Δx→0limΔxf(x+Δx)−f(x)近似求导,由此我们不需要实际计算导数的表达式,也可以从数值上进行近似。为此,求导方式的代码只需要写清楚残差怎么计算即可。
数值求导的代价函数类定义为NumericDiffCostFunction类,其函数声明为:
template <typename CostFunctor,
NumericDiffMethodType method = CENTRAL,
int kNumResiduals, // Number of residuals, or ceres::DYNAMIC.
int... Ns> // Size of each parameter block.
class NumericDiffCostFunction : public
SizedCostFunction<kNumResiduals, Ns> {
};
数值求导法也是构造代价函数结构体CostFunctor,来定义残差。但在重载括号运算符() 时,没有使用模板,类型都固定为double。在重载的()运算符形参中,最后一个为残差(唯一的非常量形参),前面几个为输入参数块。函数返回true表示成功。另一个不同点是,在实例化代价函数类时需要额外指定一个模板参数NumericDiffMethodType。
数值求导方法NumericDiffMethodType又具体分为:前向求导、中心求导和Ridders方法,对应的精度和耗时依次增加。官方建议在不考虑时间约束时采用Ridders方法,中心求导是一个均衡的选择。
下面以最小二乘 min x 1 2 ( 10 − x ) 2 \underset{x}{\min} \frac{1}{2}(10-x)^{2} xmin21(10−x)2为例自动求导。显然残差为 ( 10 − x ) (10−x) (10−x):
struct CostFunctor {
// 形参: 输入参数块, 残差
bool operator()(const double *const x, double *residual) const {
residual[0] = 10.0 - x[0];
return true;
}
};
// 模板参数: 代价函数结构体, ceres::CENTRAL, 残差维度, 输入参数块维度
ceres::CostFunction *cost_function
= new ceres::NumericDiffCostFunction<CostFunctor, ceres::CENTRAL, 1, 1>(
new CostFunctor());
下面以最小二乘 min x 1 2 ( k − x T y ) 2 \underset{x}{\min} \frac{1}{2}(k-x^Ty)^{2} xmin21(k−xTy)2为例数值求导,其中 x x x、 y y y为二维向量变量, k k k为常数。显然残差为 k − x T y k-x^Ty k−xTy:
class CostFunctor {
CostFunctor(double k): k_(k) {}
// 形参: 输入参数块, 残差
bool operator()(const double* const x,
const double* const y,
double* residuals) const {
residuals[0] = k_ - x[0] * y[0] + x[1] * y[1];
return true;
}
private:
double k_;
};
// 模板参数: 代价函数结构体, 残差维度, 输入参数块维度
ceres::CostFunction* cost_function
= new ceres::NumericDiffCostFunction<CostFunctor, ceres::CENTRAL, 1, 2, 2>(
new CostFunctor(1.0)); ^ ^ ^ ^
| | | |
Finite Differencing Scheme -+ | | |
Dimension of residual ------------+ | |
Dimension of x ----------------------+ |
Dimension of y -------------------------+
对于,ceres::NumericDiffCostFunction<CostFunctor, method, x, y, z, …>的几个模板参数与CostFunctor的括号运算符()的形参对应关系:
-
x x x决定了residuals的维度
-
y , z , . . . y, z, ... y,z,...的个数决定了输入参数块的个数,即括号运算符
()的常量形参(除最后一个形参)个数,而 y y y、 z z z本身的值决定了每个输入参数块的维度,即每个常量形参的维度 -
x x x决定了模板括号运算符
()的非常量形参(最后一个形参)的维度
求导方法的选择
求导方法的选择的依据是多方面的,一方面是精度和速度,另一方面是使用的便捷性。毫无疑问,在代码优化的情况下,解析求导方式求解速度最快,但缺点是需要人工计算雅克比矩阵,失去了便捷性。数值求导几乎是万能的,只是时间稍慢。而自动求导,虽然较为方便,但也存在问题,例如传入的变量类型若不是较为基础的数据格式则不可用自动求导。
官方给出了几种方法的计算时间如下:
| 求导方法 | 耗时 |
|---|---|
| Rat43Analytic | 255 |
| Rat43AnalyticOptimized | 92 |
| Rat43NumericDiffForward | 262 |
| Rat43NumericDiffCentral | 517 |
| Rat43NumericDiffRidders | 3760 |
| Rat43AutomaticDiff | 129 |
(多种求导方法耗时比较。从上到下:解析求导、优化后的解析求导、向前数值求导、中心数值求导、Ridders数值求导、自动求导)
可以看出,代码优化较好的解析法求导速度最快,其次是自动求导,数值求导相对较慢。
构建优化问题并求解(STEP1/3/4/5)

构建优化问题
-
声明ceres::Problem problem
-
通过AddResidualBlock()将代价函数(cost function)、核函数(loss function)和输入参数块添加到problem
这里以自动求导为例:
ceres::CostFunction *cost_function =
new ceres::AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor());
ceres::Problem problem;
problem.AddResidualBlock(cost_function, NULL, &x);
- 配置求解器,并计算,输出结果
ceres::Solver::Options options;
options.max_num_iterations = 25;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.BriefReport() << "\n";
添加残差块
一般情况下,problem对象可以调用AddResidualBlock()函数添加残差块,包括代价函数、核函数、输入参数块,该函数的原型如下:
ResidualBlockId Problem::AddResidualBlock(CostFunction *cost_function,
LossFunction *loss_function,
const vector<double *> parameter_blocks);
ResidualBlockId Problem::AddResidualBlock(CostFunction *cost_function,
LossFunction *loss_function,
double *x0, double *x1, ...);
该函数的形参含义为:
- cost_function:代价函数,包含了输入参数块的数量和大小以及输出的数量,AddResidualBlock()函数内部会检测传入的输入参数块是否和代价函数中定义的维数一致,维度不一致时程序会强制退出
- loss_function:核函数,或损失函数,用于处理参数中含有野值的情况,避免错误量测对估计的影响,常用参数包括HuberLoss、CauchyLoss等;该参数也可以取NULL或nullptr,此时损失函数为单位函数
- parameter_blocks/x0,x1…:输入参数块,可一次性传入所有参数的指针容器或依次传入所有参数的指针
例如:
double x1[] = {1.0, 2.0, 3.0};
double x2[] = {1.0, 2.0, 5.0, 6.0};
double x3[] = {3.0, 6.0, 2.0, 5.0, 1.0};
vector<double*> v1;
v1.push_back(x1);
vector<double*> v2;
v2.push_back(x2);
v2.push_back(x1);
Problem problem;
ceres::CostFunction *cost_function1 =
new ceres::AutoDiffCostFunction<CostFunctor, 1, 3>(new CostFunctor());
ceres::CostFunction *cost_function2 =
new ceres::AutoDiffCostFunction<CostFunctor, 1, 4, 3>(new CostFunctor());
problem.AddResidualBlock(cost_function1, nullptr, x1);
problem.AddResidualBlock(cost_function2, nullptr, x2, x1);
problem.AddResidualBlock(cost_function1, nullptr, v1);
problem.AddResidualBlock(cost_function2, nullptr, v2);
problem对象也可以调用AddParameterBlock()显式添加输入参数块,这会导致额外的正确性检查;但是,如果参数块不存在,AddResidualBlock()会隐式添加它们,因此不需要显式调用AddParameterBlock()。
也就是说,AddResidualBlock()在添加残差块的同时,该函数内部已经隐式地调用了AddParameterBlock()函数进行参数块的设置。但在一些情况下,如果想要显示地传入参数模(通常出现在需要对优化参数进行重新参数化的情况),可以使用AddParameterBlock()函数:
void Problem::AddParameterBlock(double *values, int size);
void Problem::AddParameterBlock(double *values, int size,
LocalParameterization *local_parameterization);
void Problem::AddParameterBlock(double *values, int size, Manifold *manifold);
其中,第一种函数原型除了会增加一些额外的参数检查之外,功能上和隐式地进行参数块的设置并没有太大区别。第二/三种函数原型则会额外传入LocalParameterization/Manifold,用于重构优化参数的维数。在2.2.0版本之后,LocalParameterization接口被弃用,需要使用Manifold代替。
注意:problem内的参数块使用map进行管理,无论添加多少次,都不会重复。
核函数
对于最小二乘问题,最小化可能会遇到包含异常值的输入项,即完全虚假的测量值,因此使用损失函数来减少其影响非常重要。
自定义核函数类需要继承基类LossFunction,并对其中的纯虚函数进行实现。当然也可以使用Ceres预先定义好的较常用的子类。
class LossFunction {
public:
virtual void Evaluate(double s, double out[3]) const = 0;
};
关键方法是LossFunction::Evaluate(),它给定一个非负标量
s
s
s,核函数
ρ
\rho
ρ,计算:
o u t = [ ρ ( s ) , ρ ′ ( s ) , ρ ′ ′ ( s ) ] out = \begin{bmatrix}\rho(s), & \rho'(s), & \rho''(s)\end{bmatrix} out=[ρ(s),ρ′(s),ρ′′(s)]
其中, s s s是残差的平方。
下面以柯西核函数(ceres预先定义好的CauchyLoss)为例:
// Inspired by the Cauchy distribution
// rho(s) = log(1 + s).
// At s = 0: rho = [0, 1, -1].
class CERES_EXPORT CauchyLoss : public LossFunction {
public:
// 可以看出形参a为尺度参数
explicit CauchyLoss(double a) : b_(a * a), c_(1 / b_) {}
void Evaluate(double, double*) const override;
private:
// b = a^2
const double b_;
// c = 1 / a^2
const double c_;
};
void CauchyLoss::Evaluate(double s, double rho[3]) const {
const double sum = 1.0 + s * c_;
const double inv = 1.0 / sum;
// 'sum' and 'inv' are always positive, assuming that 's' is.
rho[0] = b_ * log(sum);
rho[1] = std::max(std::numeric_limits<double>::min(), inv);
rho[2] = - c_ * (inv * inv);
}
Ceres预定义的一些LossFunction。为了简单起见,我们描述了它们的未缩放版本。下图以图形方式说明了它们的形状。
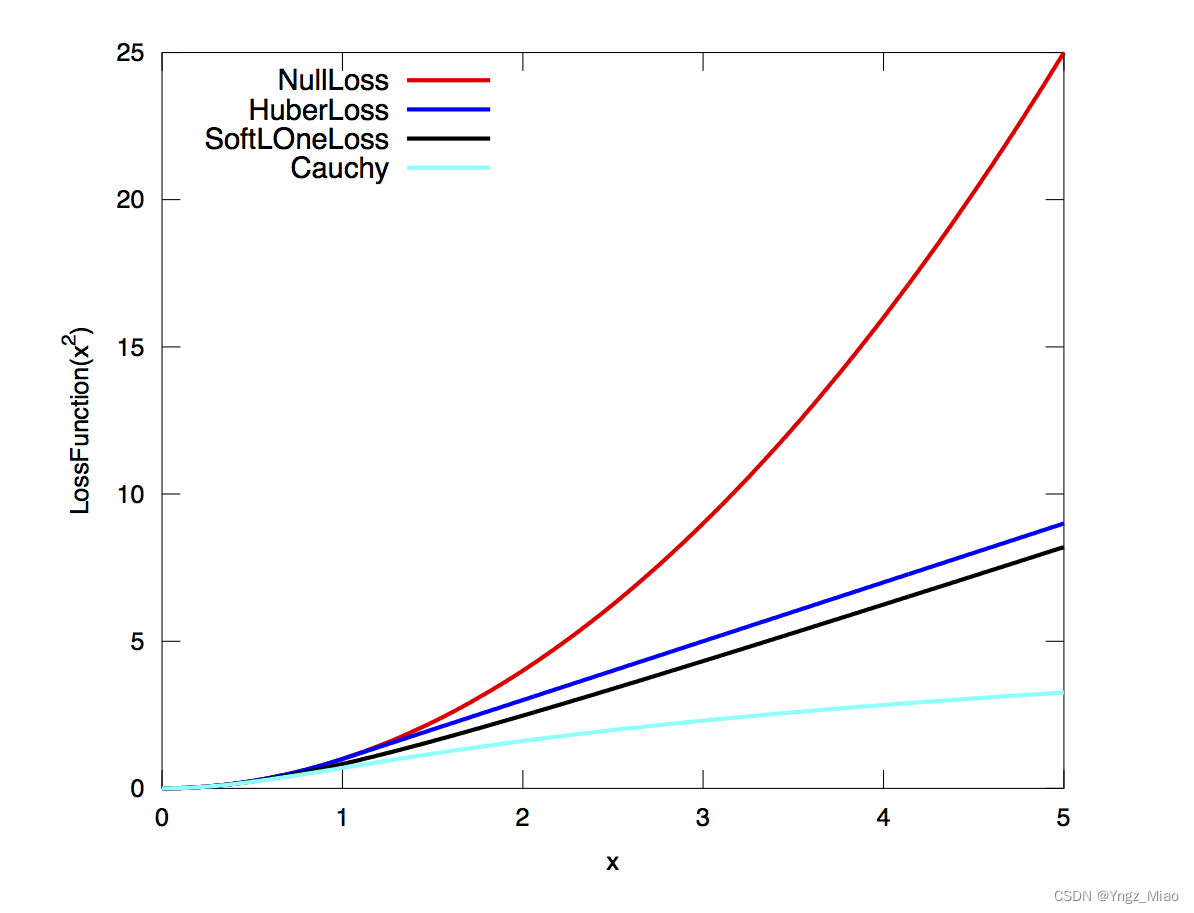
下面梳理一下常见的损失函数:
| LossFunction类别 | 公式 |
|---|---|
| TrivialLoss | ρ ( s ) = s \rho(s) = s ρ(s)=s |
| HuberLoss | ρ ( s ) = { s s ≤ 1 2 s − 1 s > 1 \rho(s) = \begin{cases} s & s \le 1\\ 2 \sqrt{s} - 1 & s > 1 \end{cases} ρ(s)={s2s−1s≤1s>1 |
| SoftLOneLoss | ρ ( s ) = 2 ( 1 + s − 1 ) \rho(s) = 2 (\sqrt{1+s} - 1) ρ(s)=2(1+s−1) |
| CauchyLoss | ρ ( s ) = log ( 1 + s ) \rho(s) = \log(1 + s) ρ(s)=log(1+s) |
| ArctanLoss | ρ ( s ) = arctan ( s ) \rho(s) = \arctan(s) ρ(s)=arctan(s) |
| TolerantLoss | ρ ( s , a , b ) = b log ( 1 + e ( s − a ) / b ) − b log ( 1 + e − a / b ) \rho(s,a,b) = b \log(1 + e^{(s - a) / b}) - b \log(1 + e^{-a / b}) ρ(s,a,b)=blog(1+e(s−a)/b)−blog(1+e−a/b) |
LocalParameterization
LocalParameterization类的作用是解决非线性优化中的过参数化问题。所谓过参数化,即输入参数块的实际自由度小于参数本身的自由度。
除了上文的AddParameterBlock()函数之外,还可以用下面的函数设置:
void Problem::SetParameterization(double *values,
LocalParameterization *local_parameterization);
例如,在SLAM中,许多优化问题中,尤其是传感器融合问题,必须对存在于被称为流形的空间中的量进行建模。流形空间,局部看起来像欧几里得空间。更准确地说,流形上的每个点都有一个与流形相切的线性空间。它的尺寸等于流形本身的固有尺寸,该固有尺寸小于或等于嵌入流形的周围空间。例如,三维空间中球体上一点的切线空间是与该点处的球体相切的二维平面。切线空间有趣的原因有两个:
- 它们是欧几里得空间,因此通常的向量空间运算适用于那里,这使得数值运算变得容易
- 切线空间中的运动转化为沿流形的运动,垂直于切空间的运动不会转化为流形上的运动
例如:在SLAM的优化问题中,采用单位四元数表示位姿时,由于单位四元数本身的约束(模长为1),实际的自由度为3而非4。同时,单位四元数/旋转矩阵并不支持广义的加法运算,即使用普通的加法就会打破其constraint,比如,旋转矩阵加旋转矩阵得到的就不再是旋转矩阵,单位四元数加上单位四元数就不再是单位四元数。
因此,我们在使用ceres对其进行迭代更新的时候就需要自定义其更新方式了,此时就需要使用到LocalParameterization。
LocalParaneterization本身是一个虚基类,用户在自行定义使用的子类时,需要将所有的纯虚函数都实现一遍。当然也可以使用Ceres预先定义好的较常用的子类。
class LocalParameterization {
public:
virtual ~LocalParameterization() {}
// 流型空间中的加法,即参数正切空间上的更新函数
virtual bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const = 0;
// 计算雅克比矩阵
virtual bool ComputeJacobian(const double* x, double* jacobian) const = 0;
// 一般不用
virtual bool MultiplyByJacobian(const double* x,
const int num_rows,
const double* global_matrix,
double* local_matrix) const;
// 参数块的实际维数,可能存在冗余
virtual int GlobalSize() const = 0;
// 参数块在正切空间上的维数
virtual int LocalSize() const = 0;
};
下面以单位四元数(ceres预先定义好的QuaternionParameterization)为例,解释如何实现参数本地化。
由于由单位四元数表示的传感器的旋转/方向,它的实际维数为4,但是正切空间上的维数为3。因此,增量 d e l t a delta delta就是一个3维的。那单位四元数怎么和3维表示的 d e l t a delta delta进行计算呢?旋转向量(它正好就是3维的,且与单位四元数之间可以相互转化)。流型中的加法可以用符号 ⊞ \boxplus ⊞ 表示。
设单位四元数 s = [ w , x , y , z ] s=[w,x,y,z] s=[w,x,y,z],对应的旋转向量为 ϕ = [ p , q , r ] \phi = [p,q,r] ϕ=[p,q,r] ,定义 θ = p 2 + q 2 + r 2 \theta=\sqrt{p^{2}+q^{2}+r^{2}} θ=p2+q2+r2 ,是 ϕ \phi ϕ 的模(旋转角), ∣ ∣ a ∧ ∣ ∣ = 1 ||a^{\wedge}|| = 1 ∣∣a∧∣∣=1,是 ϕ \phi ϕ 的方向向量(旋转轴), 即 ϕ = θ a ∧ \phi = \theta a^{\wedge} ϕ=θa∧,其中 ∧ \wedge ∧为向量到反对称矩阵的转换符。
旋转向量到单位四元数的映射为:
[ c o s ( θ ) , s i n ( θ ) θ p , s i n ( θ ) θ q , s i n ( θ ) θ r ] \Big[cos(\theta), \frac{sin(\theta)}{\theta}p, \frac{sin(\theta)}{\theta}q, \frac{sin(\theta)}{\theta}r \Big] [cos(θ),θsin(θ)p,θsin(θ)q,θsin(θ)r]
单位四元数相对于旋转矢量的雅克比矩阵计算方法,即:
J 4 × 3 = d s / d ϕ = d [ w , x , y , z ] T / d [ p , q , r ] \mathcal{J}_{4 \times 3}=d \mathcal{s} / d \mathcal{\phi} = d [w, x, y, z]^T /d [p,q,r] J4×3=ds/dϕ=d[w,x,y,z]T/d[p,q,r]
对应Jacobian维数为4行3列。这部分的详细推导可以参考:【Ceres】(二)LocalParameterization参数化、[ceres-solver] From QuaternionParameterization to LocalParameterization 、优化库——ceres(二)深入探索ceres::Problem
。
class CERES_EXPORT QuaternionParameterization : public LocalParameterization {
public:
virtual ~QuaternionParameterization() {}
// 重载的Plus函数给出了四元数的更新方法
// 参数:优化前的四元数x,用旋转向量表示的增量delta,以及更新后的四元数x_plus_delta。
// 函数首先将增量delta由旋转向量转换为四元数,随后采用标准四元数乘法对四元数进行更新
virtual bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const;
// 计算雅可比矩阵,存储方式为行优先
virtual bool ComputeJacobian(const double* x,
double* jacobian) const;
// 四元数本身的实际维数为4,但在内部优化时,ceres采用的是旋转向量,维数为3
// GlobalSize:真正的维数是一个4维的
virtual int GlobalSize() const { return 4; }
// LocalSize:ceres优化时使用的维数是一个3维的
virtual int LocalSize() const { return 3; }
};
bool QuaternionParameterization::Plus(const double* x,
const double* delta,
double* x_plus_delta) const {
// 将旋转矢量转换为四元数形式
const double norm_delta =
sqrt(delta[0] * delta[0] + delta[1] * delta[1] + delta[2] * delta[2]);
if (norm_delta > 0.0) {
const double sin_delta_by_delta = (sin(norm_delta) / norm_delta);
double q_delta[4];
q_delta[0] = cos(norm_delta);
q_delta[1] = sin_delta_by_delta * delta[0];
q_delta[2] = sin_delta_by_delta * delta[1];
q_delta[3] = sin_delta_by_delta * delta[2];
// 采用四元数乘法更新
QuaternionProduct(q_delta, x, x_plus_delta);
} else {
for (int i = 0; i < 4; ++i) {
x_plus_delta[i] = x[i];
}
}
return true;
}
// 雅可比矩阵是4*3维的,代码里使用一个size为12的数组存储
bool QuaternionParameterization::ComputeJacobian(const double* x,
double* jacobian) const {
jacobian[0] = -x[1]; jacobian[1] = -x[2]; jacobian[2] = -x[3];
jacobian[3] = x[0]; jacobian[4] = x[3]; jacobian[5] = -x[2];
jacobian[6] = -x[3]; jacobian[7] = x[0]; jacobian[8] = x[1];
jacobian[9] = x[2]; jacobian[10] = -x[1]; jacobian[11] = x[0];
return true;
}
下面看下LocalParaneterization的具体用法。例如:在SLAM中,若使用四元数进行优化,可以使用Ceres预先定义的QuaternionParameterization对优化参数进行重构:
problem.AddParameterBlock(quaternion, 4); // 直接传递4维参数
ceres::LocalParameterization* local_param =
new ceres::QuaternionParameterization();
// 重构参数,优化时实际使用的是3维的等效旋转矢量(参数map管理)
problem.AddParameterBlock(quaternion, 4, local_param);
Ceres预定义的一些LocalParaneterization:
| LocalParaneterization类别 | 含义 |
|---|---|
| QuaternionParameterization | 四元数 |
| EigenQuaternionParameterization | 除四元数排序采用Eigen的实部最后外,与QuaternionParameterization完全一致 |
| IdentityParameterizationconst | LocalSize与GlobalSize一致,相当于不传入LocalParameterization |
| SubsetParameterization | GlobalSize为2,LocalSize为1,用于第一维不需要优化的情况 |
| HomogeneousVectorParameterization | 具有共面约束的空间点 |
| ProductParameterization | 7维位姿变量一同优化,而前4维用四元数表示的情况 |
Manifold
在2.2.0版本之后,LocalParameterization接口被弃用,需要使用Manifold代替。它们之间的使用场景/使用方法很多都是类似的。这里就不详细介绍了。
除了上文的AddParameterBlock()函数之外,还可以用下面的函数设置:
void Problem::SetManifold(double *values, Manifold *manifold);
class Manifold {
public:
virtual ~Manifold();
// 参数块的实际维数,可能存在冗余
virtual int AmbientSize() const = 0;
// 参数块在正切空间上的维数
virtual int TangentSize() const = 0;
// 流型空间中的加法,即参数正切空间上的更新函数
virtual bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const = 0;
// 计算雅克比矩阵
virtual bool PlusJacobian(const double* x, double* jacobian) const = 0;
// 一般不用
virtual bool RightMultiplyByPlusJacobian(const double* x,
const int num_rows,
const double* ambient_matrix,
double* tangent_matrix) const;
// 流型空间中的减法,即参数正切空间上的更新函数
virtual bool Minus(const double* y,
const double* x,
double* y_minus_x) const = 0;
// 计算雅克比矩阵
virtual bool MinusJacobian(const double* x, double* jacobian) const = 0;
};
Options类
Solver::Options含有的参数种类繁多,但是在大多数情况下,绝大多数参数我们都会使用Ceres的默认设置,这里只列出一些常用或较为重要的参数:
- minimizer_type:迭代求解方法,可选线性搜索方法(
LINEAR_SEARCH)或信赖域方法(TRUST_REGION),默认为TRUST_REGION方法;由于大多数情况我们都会选择LM或DOGLEG方法,该选项一般直接采用默认值 - trust_region_strategy_type:信赖域策略,可选
LEVENBERG_MARQUARDT或DOGLEG,默认为LEVENBERG_MARQUARDT - linear_solver_type:信赖域方法中求解线性方程组所使用的求解器类型,默认为
DENSE_QR,其他可选项如下:DENSE_QR(QR分解,用于小规模最小二乘问题求解)、DENSE_NORMAL_CHOLESKY&SPARSE_NORMAL_CHOLESKY(Cholesky分解,用于具有稀疏性的大规模非线性最小二乘问题求解)、CGNR(使用共轭梯度法求解稀疏方程)、DENSE_SCHUR&SPARSE_SCHUR(SCHUR分解,用于BA问题求解)、ITERATIVE_SCHUR(使用共轭梯度SCHUR求解BA问题) - linear_solver_ordering:线性方程求解器的消元顺序,默认为NULL,即由Ceres自行决定消元顺序
- min_linear_solver_iteration/max_linear_solver_iteration:线性求解器的最小/最大迭代次数,默认为0/500,一般不需要更改
- max_num_iterations:求解器的最大迭代次数
- max_solver_time_in_seconds:求解器的最大运行秒数
- num_threads:Ceres求解时使用的线程数,在老版本的Ceres中还有一个针对线性求解器的线程设置选项,num_linear_solver_threads,最新版本的Ceres中该选项已被取消;虽然为了保证程序的兼容性,用户依旧可以设置该参数,但Ceres会自动忽略该参数,并没有实际意义
Summary类
Solver::Summary包含了求解器本身和求解中各变量的信息,许多成员函数与Solver::Options一致,这里只给出两个常用的成员函数:
// 输出单行的简单总结
string Solver::Summary::BriefReport() const;
// 输出多行的完整总结
string Solver::Summary::FullReport() const;
ceres实战案例
CmakeLists.txt配置
cmake_minimum_required(VERSION 2.8)
project(ceres)
find_package(Ceres REQUIRED)
include_directories(${CERES_INCLUDE_DIRS})
add_executable(test test.cpp)
target_link_libraries(test ${CERES_LIBRARIES})
示例:ceres入门例子
一个简单的求解 min x 1 2 ( 10 − x ) 2 \underset{x}{\min} \frac{1}{2}(10-x)^{2} xmin21(10−x)2 的优化问题,代码如下:
#include<iostream>
#include<ceres/ceres.h>
// 第一部分:构建代价函数结构体,重载()符号
struct CostFunctor {
template <typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = T(10.0) - x[0];
return true;
}
};
// 主函数
int main(int argc, char** argv) {
// 寻优参数x的初始值,为5
double initial_x = 5.0;
double x = initial_x;
// 第二部分:构建寻优问题
ceres::Problem problem;
// 使用自动求导,将之前的代价函数结构体传入,第一个1是输出维度,即残差的维度,第二个1是输入维度,即待寻优参数x的维度
ceres::CostFunction* cost_function =
new ceres::AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
// 向问题中添加误差项,本问题比较简单,添加一个就行
problem.AddResidualBlock(cost_function, NULL, &x);
// 第三部分: 配置并运行求解器
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR; //配置增量方程的解法
options.minimizer_progress_to_stdout = true; //输出到cout
ceres::Solver::Summary summary; //优化信息
ceres::Solve(options, &problem, &summary); //求解!!!
std::cout << summary.BriefReport() << "\n"; //输出优化的简要信息
// 最终结果
std::cout << "x : " << initial_x << " -> " << x << "\n";
return 0;
}
示例:曲线拟合
拟合非线性函数的曲线 y = e a x 2 + b x + c y=e^{a x^{2}+b x+c} y=eax2+bx+c(其中, a = 3 a=3 a=3、 b = 2 b=2 b=2、 c = 1 c=1 c=1,待拟合数据点: [ 0 , 1 ] [0,1] [0,1]之间均匀生成的1000个数据点,加上方差为1的白噪声)。代码如下:
#include<iostream>
#include<opencv2/core/core.hpp>
#include<ceres/ceres.h>
// 构建代价函数结构体,abc为输入参数块,residual为残差。
struct CURVE_FITTING_COST
{
CURVE_FITTING_COST(double x, double y): _x(x), _y(y) {}
template <typename T>
bool operator()(const T* const abc, T* residual) const {
residual[0] = _y - ceres::exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
return true;
}
const double _x, _y;
};
// 主函数,abc初始化为0
int main()
{
// 参数初始化设置,
double abc[3] = {0, 0, 0};
// 生成待拟合曲线的数据散点,储存在Vector里
std::vector<double> x_data, y_data;
double a = 3, b = 2, c = 1, w = 1;
cv::RNG rng;
for (int i = 0; i < 1000; i++) {
double x = i / 1000.0;
x_data.push_back(x);
y_data.push_back(exp(a * x * x + b * x + c) + rng.gaussian(w));
}
// 反复使用AddResidualBlock方法,将每个点的残差累计求和构建最小二乘优化式
// 不使用核函数,输入参数块是abc
ceres::Problem problem;
for (int i = 0; i < 1000; i++) {
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
new CURVE_FITTING_COST(x_data[i], y_data[i])), nullptr, abc);
}
// 配置求解器并求解,输出结果
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << "a= " << abc[0] << std::endl;
std::cout << "b= " << abc[1] << std::endl;
std::cout << "c= " << abc[2] << std::endl;
return 0;
}
详细可以参考文章:一文助你Ceres 入门——Ceres Solver新手向全攻略。
示例:最小化鲍威尔方程
假设
x
=
[
x
1
,
x
2
,
x
3
,
x
4
]
x=[x_1,x_2,x_3,x_4]
x=[x1,x2,x3,x4],它的方程表示为
F
(
x
)
=
[
f
1
(
x
)
,
f
2
(
x
)
,
f
3
(
x
)
,
f
4
(
x
)
]
F(x)=[f_1(x),f_2(x),f_3(x),f_4(x)]
F(x)=[f1(x),f2(x),f3(x),f4(x)]:
f
1
(
x
)
=
x
1
+
10
x
2
f
2
(
x
)
=
5
(
x
3
−
x
4
)
f
3
(
x
)
=
(
x
2
−
2
x
3
)
2
f
4
(
x
)
=
10
(
x
1
−
x
4
)
2
\begin{split} f_1(x)=x_1+10x_2 \\ f_2(x)=\sqrt{5}(x_3-x_4) \\ f_3(x)=(x_2-2x_3)^2 \\ f_4(x)=\sqrt{10}(x_1-x_4)^2 \end{split}
f1(x)=x1+10x2f2(x)=5(x3−x4)f3(x)=(x2−2x3)2f4(x)=10(x1−x4)2
找到一组
x
x
x使得
1
2
∥
F
(
x
)
∥
2
\frac{1}{2}\left\|F(x)\right\|^2
21∥F(x)∥2最小。代码如下:
#include <vector>
#include "ceres/ceres.h"
//创建四个残差块,也就是四个仿函数
struct F1 {
template <typename T>
bool operator()(const T* const x1, const T* const x2, T* residual) const {
residual[0] = x1[0] + 10.0 * x2[0];
return true;
}
};
struct F2 {
template <typename T>
bool operator()(const T* const x3, const T* const x4, T* residual) const {
residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
return true;
}
};
struct F3 {
template <typename T>
bool operator()(const T* const x2, const T* const x3, T* residual) const {
residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
return true;
}
};
struct F4 {
template <typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};
int main(int argc, char** argv) {
// 设置初始值
double x1 = 3.0;
double x2 = -1.0;
double x3 = 0.0;
double x4 = 1.0;
// 加入problem
ceres::Problem problem;
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F1, 1, 1, 1>(new F1), NULL, &x1, &x2);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F2, 1, 1, 1>(new F2), NULL, &x3, &x4);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F3, 1, 1, 1>(new F3), NULL, &x2, &x3);
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<F4, 1, 1, 1>(new F4), NULL, &x1, &x4);
// 设置options
ceres::Solver::Options options;
options.max_num_iterations = 100; // 迭代次数
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.FullReport() << "\n";
std::cout << "Final x1 = " << x1
<< ", x2 = " << x2
<< ", x3 = " << x3
<< ", x4 = " << x4
<< "\n";
return 0;
}
详细可以参考文章:Ceres Solver:从入门到使用。
这样看起来有点复杂,把输入参数块和残差全部拆开来了,也可以合并起来看:
#include <vector>
#include "ceres/ceres.h"
//创建四个残差块,也就是四个仿函数
struct CostFunctor {
template <typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = x[0] + 10.0 * x[1];
residual[1] = sqrt(5.0) * (x[2] - x[3]);
residual[2] = (x[1] - 2.0 * x[2]) * (x[1] - 2.0 * x[2]);
residual[3] = sqrt(10.0) * (x[0] - x[3]) * (x[0] - x[3]);
return true;
}
};
int main(int argc, char** argv) {
// 设置初始值
double x = {3.0, -1.0, 0.0, 1.0};
// 加入problem
ceres::Problem problem;
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<CostFunctor, 4, 4>(new CostFunctor),
NULL, &x);
// 设置options
ceres::Solver::Options options;
options.max_num_iterations = 100; // 迭代次数
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.FullReport() << "\n";
std::cout << "Final x1 = " << x[0]
<< ", x2 = " << x[1]
<< ", x3 = " << x[2]
<< ", x4 = " << x[3]
<< "\n";
return 0;
}
示例: 基于李代数的视觉SLAM位姿优化
基于李代数进行视觉SLAM位姿优化时,可以得到:
- 残差(预测值 - 观测值)
r ( ξ ) = K exp ( ξ ∧ ) P − u r(\xi)=K \exp \left(\xi^{\wedge}\right) P-u r(ξ)=Kexp(ξ∧)P−u
- 雅克比矩阵
J = ∂ r ( ξ ) ∂ ξ = [ f x Z ′ 0 − X ′ f x Z ′ 2 − X ′ Y ′ f z Z 2 f x + X ′ 2 f x Z 2 − Y ′ f x Z ′ 0 f y Z ′ − Y ′ f y Z 2 − f y − Y ′ 2 f y Z ′ 2 X ′ Y ′ f y Z ′ 2 X ′ f y Z ′ ] ∈ R 2 × 6 \begin{array}{c} J &= &\frac{\partial r(\xi)}{\partial \xi} \\ &= &\left[\begin{array}{ccccc} \frac{f_{x}}{Z^{\prime}} & 0 & -\frac{X^{\prime} f_{x}}{Z^{\prime 2}} & -\frac{X^{\prime} Y^{\prime} f_{z}}{Z^{2}} & f_{x}+\frac{X^{\prime 2} f_{x}}{Z^{2}} & -\frac{Y^{\prime} f_{x}}{Z^{\prime}} \\ 0 & \frac{f_{y}}{Z^{\prime}} & -\frac{Y^{\prime} f_{y}}{Z^{2}} & -f_{y}-\frac{Y^{\prime 2} f_{y}}{Z^{\prime 2}} & \frac{X^{\prime} Y^{\prime} f_{y}}{Z^{\prime 2}} & \frac{X^{\prime} f_{y}}{Z^{\prime}} \end{array}\right] \in \mathbb{R}^{2 \times 6} \end{array} J==∂ξ∂r(ξ)[Z′fx00Z′fy−Z′2X′fx−Z2Y′fy−Z2X′Y′fz−fy−Z′2Y′2fyfx+Z2X′2fxZ′2X′Y′fy−Z′Y′fxZ′X′fy]∈R2×6
该雅可比矩阵的求解方式,可以参考文章:视觉SLAM位姿优化时误差函数雅克比矩阵的计算、BA优化中Jacobian矩阵的计算
核心代码如下:
代价函数的构造:
// 重投影误差,残差2维的,优化变量是6维度
class BAGNCostFunctor : public ceres::SizedCostFunction<2, 6> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW //对齐
// 第一个是像素观测值,第二个是准备用来重投影的三维点
BAGNCostFunctor(Eigen::Vector2d observed_p, Eigen::Vector3d observed_P) :
observed_p_(observed_p), observed_P_(observed_P) {}
virtual ~BAGNCostFunctor() {}
// 输入参数块、残差、雅可比矩阵
virtual bool Evaluate(double const* const* parameters,
double *residuals, double **jacobians) const {
// 获取位姿,并将三维点进行重投影到成像平面
Eigen::Map<const Eigen::Matrix<double, 6, 1> > T_se3(*parameters);
Sophus::SE3 T_SE3 = Sophus::SE3::exp(T_se3);
Eigen::Vector3d Pc = T_SE3 * observed_P_;
// 内参矩阵
Eigen::Matrix3d K;
double fx = 520.9, fy = 521.0, cx = 325.1, cy = 249.7;
K << fx, 0, cx, 0, fy, cy, 0, 0, 1;
// 计算残差
Eigen::Vector2d residual = observed_p_ - (K * Pc).hnormalized();
residuals[0] = residual[0];
residuals[1] = residual[1];
if(jacobians != NULL) {
if(jacobians[0] != NULL) {
// 2*6的雅克比矩阵
Eigen::Map<Eigen::Matrix<double, 2, 6, Eigen::RowMajor> > J(jacobians[0]);
double x = Pc[0];
double y = Pc[1];
double z = Pc[2];
double x2 = x * x;
double y2 = y * y;
double z2 = z * z;
J(0,0) = fx / z;
J(0,1) = 0;
J(0,2) = -fx * x / z2;
J(0,3) = -fx * x * y / z2;
J(0,4) = fx + fx * x2 / z2;
J(0,5) = -fx * y / z;
J(1,0) = 0;
J(1,1) = fy / z;
J(1,2) = -fy * y / z2;
J(1,3) = -fy - fy * y2 / z2;
J(1,4) = fy * x * y / z2;
J(1,5) = fy * x / z;
}
}
return true;
}
private:
const Eigen::Vector2d observed_p_;
const Eigen::Vector3d observed_P_;
};
构造优化问题,并求解相机位姿:
Sophus::Vector6d se3;
// 在当前problem中添加代价函数残差块,损失函数为NULL采用默认的最小二乘误差即L2范数,优化变量为 se3
ceres::Problem problem;
for(int i = 0; i < n_points; ++i) {
ceres::CostFunction *cost_function;
cost_function = new BAGNCostFunctor(p2d[i], p3d[i]);
problem.AddResidualBlock(cost_function, NULL, se3.data());
}
ceres::Solver::Options options;
options.dynamic_sparsity = true;
options.max_num_iterations = 100; // 迭代100次
options.sparse_linear_algebra_library_type = ceres::SUITE_SPARSE;
options.minimizer_type = ceres::TRUST_REGION;
options.linear_solver_type = ceres::SPARSE_NORMAL_CHOLESKY;
options.trust_region_strategy_type = ceres::DOGLEG;
options.minimizer_progress_to_stdout = true;
options.dogleg_type = ceres::SUBSPACE_DOGLEG;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.BriefReport() << "\n";
std::cout << "estimated pose: \n" << Sophus::SE3::exp(se3).matrix() << std::endl;
详细可以参考文章:Ceres-Solver 从入门到上手视觉SLAM位姿优化问题。
相关阅读
- Ceres Solver官方文档
- Ceres详解(一) Problem类
- 优化库——ceres(一)快速概览