❓ 132. 分割回文串 II
难度:困难
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = “aab”
输出:1
解释:只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。
示例 2:
输入:s = “a”
输出:0
示例 3:
输入:s = “ab”
输出:1
提示:
- 1 < = s . l e n g t h < = 2000 1 <= s.length <= 2000 1<=s.length<=2000
s仅由小写英文字母组成
💡思路:动态规划
- 定义一个二维数组
isPalindromic[i][j],记录[i, j]是不是回文子串- 该二维数组从右下角开始遍历,如果
s[i] == s[j]则判断j - i <= 1或者 判断内部isPalindromic[i + 1][j - 1]是否是回文字符串
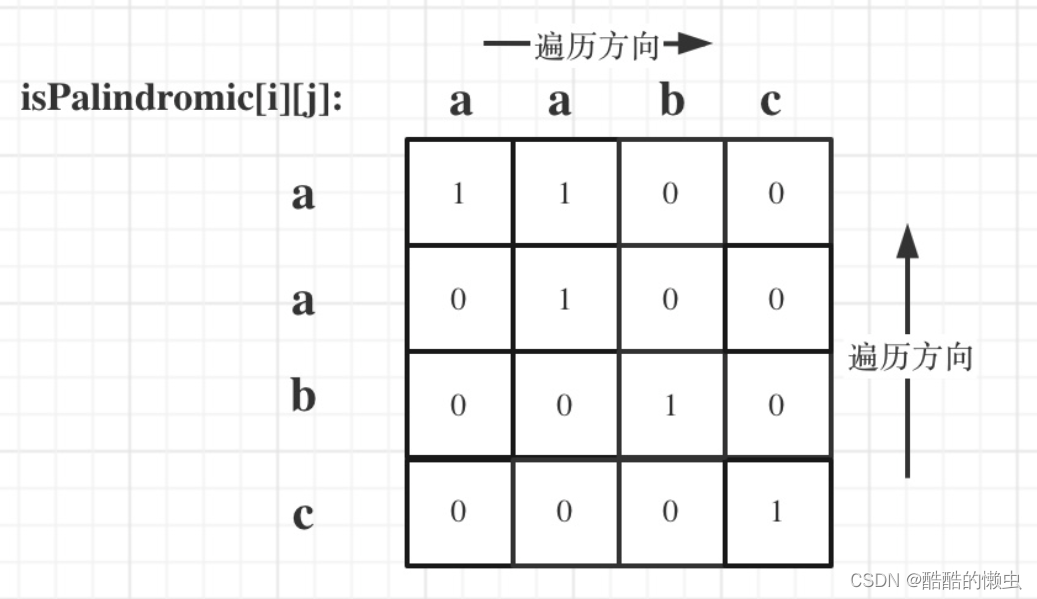
- 该二维数组从右下角开始遍历,如果
- 定义一维
dp数组,dp[i]表示使范围是[0, i]的子串分割成回文串,最少分割次数是dp[i]:- 如果要对长度为
[0, i]的子串进行分割,分割点为j:- 如果分割后,区间
[j + 1, i]是回文子串,那么dp[i]就等于dp[j] + 1; - 我们要找做小分割数量所以递推公式为: d p [ i ] = m i n ( d p [ i ] , d p [ j ] + 1 ) dp[i] = min(dp[i], dp[j] + 1) dp[i]=min(dp[i],dp[j]+1)
- 如果分割后,区间
- 如果要对长度为
- 最后
dp[n - 1]即为 所求 最少分割次数。
🍁代码:(C++、Java)
C++
class Solution {
public:
int minCut(string s) {
int n = s.size();
vector<vector<bool>> isPalindromic(n, vector<bool>(n, false));//二维数组,isPalindromic[i][j]表示[i, j]是不是回文子串
for(int i = n - 1; i >= 0; i--){
for(int j = i; j < n; j++){
if(s[i] == s[j] && (j - i <= 1 || isPalindromic[i + 1][j - 1])){
isPalindromic[i][j] = true;
}
}
}
//初始化dp数组,dp[i]表示范围是[0, i]的回文子串,最少分割次数是dp[i]
vector<int> dp(n);
for(int i = 0; i < n; i++) dp[i] = i;
for(int i = 1; i < n; i++){
if(isPalindromic[0][i])
{
dp[i] = 0;
continue;
}
for(int j = 0; j < i; j++){
if(isPalindromic[j + 1][i]){
dp[i] = min(dp[i], dp[j] + 1);
}
}
}
return dp[n - 1];
}
};
Java
class Solution {
public int minCut(String s) {
int n = s.length();
boolean[][] isPalindromic = new boolean[n][n];//二维数组,isPalindromic[i][j]表示[i, j]是不是回文子串
for(int i = n - 1; i >= 0; i--){
for(int j = i; j < n; j++){
if(s.charAt(i) == s.charAt(j) && (j - i <= 1 || isPalindromic[i + 1][j - 1])){
isPalindromic[i][j] = true;
}
}
}
//初始化dp数组,dp[i]表示范围是[0, i]的回文子串,最少分割次数是dp[i]
int[] dp = new int[n];
for(int i = 0; i < n; i++) dp[i] = i;
for(int i = 1; i < n; i++){
if(isPalindromic[0][i])
{
dp[i] = 0;
continue;
}
for(int j = 0; j < i; j++){
if(isPalindromic[j + 1][i]){
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[n - 1];
}
}
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度:
O
(
n
2
)
O(n^2)
O(n2),其中
n为字符串s的长度。预处理计算isPalindromic和动态规划计算dp的时间复杂度均为 O ( n 2 ) O(n^2) O(n2)。 - 空间复杂度:
O
(
n
2
)
O(n^2)
O(n2),数组
isPalindromic需要使用 O ( n 2 ) O(n^2) O(n2) 的空间, 数组dp需要使用 O ( n ) O(n) O(n) 的空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!