Ⅰ. 前言

​ skiplist是一种随机化的数据结构，基于并联的链表，实现简单，插入、删除、查找的复杂度均为 O(logN)（大多数情况下，因为是实现上是概率问题），因为其性能匹敌红黑树且实现较为简单，因此在很多著名项目都用 skiplist 来代替红黑树，例如 LevelDB、RocksDB、Redis中的有序集合zset 的底层存储结构就是用的skiplist。

​ 目前常用的 key-value 数据结构有三种：哈希表、红黑树、skiplist，它们各自有着不同的优缺点：

• 哈希表：插入、查找最快，为O(1)；如使用链表实现则可实现无锁；数据有序化需要显式的排序操作，即哈希表是无序的。

• 红黑树：插入、查找为O(logn)，但常数项较小；无锁实现的复杂性很高，一般需要加锁；数据天然有序。

• skiplist：插入、查找为O(logn)，但常数项比红黑树要大；底层结构为链表，可无锁实现；数据天然有序。

Ⅱ. 跳表（skiplist）

1、什么是跳表

​ skiplist 本质上也是一种查找结构，是一个“概率型”的数据结构，用于解决算法中的查找问题 （Searching），即根据给定的 key，快速查到它所在的位置（或者对应的 value ）。

​ 跳表是在 1989 年由 William Pugh 发明的，作者时年 29 岁。skiplist 发明的 初衷是为了克服平衡树的一些缺点，比如平衡树在节点插入时，需要额外的进行的树的转枝，剪枝操作，才能够达到树的平衡。而 skiplist 借助于其独特的设计，在数据插入过程中，不需要额外的数据排序过程，只需要找到其需要插入位置的前置节点，即可插入，插入之后，依然保持数据结构的数据平衡。

​ 他在论文《Skip lists: a probabilistic alternative to balanced trees》中详细介绍了跳表的数据结构和插入删除等操作。论文是这么介绍跳表的：

​ Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

​ 翻译：跳表是一种可以用来代替平衡树的数据结构。跳表使用概率平衡而不是严格强制的平衡，因此，跳表中的插入和删除算法比平衡树的等效算法简单得多，速度也快得多。

2、跳表的发明历程

​ skiplist，顾名思义，首先它是一个 list。实际上，它是在有序链表的基础上发展起来的。如果是一个有序的链表，查找数据的时间复杂度是O(N)。所以 William Pugh 开始想出了下面的优化思路：

1. 假如我们每相邻两个节点升高一层，增加一个指针，让指针指向下下个节点，如下图所示中的b。这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了，需要比较的节点数大概只有原来的一半。
2. 以此类推，我们可以在第二层新产生的链表上，继续为每相邻的两个节点升高一层，增加一个指针，从而产生第三层链表。如下图中的c，这样搜索效率就进一步提高了。
3. skiplist 正是受这种多层链表的想法的启发而设计出来的。实际上，按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似二分查找，使得查找的时间复杂度可以降低到O(log n)。但是这个结构在插入删除数据的时候有很大的问题，插入或者删除一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n)。

4. skiplist 的设计为了避免这种问题，做了一个大胆的处理，不再严格要求对应比例关系，而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数，这样就好处理多了。细节过程入下图：

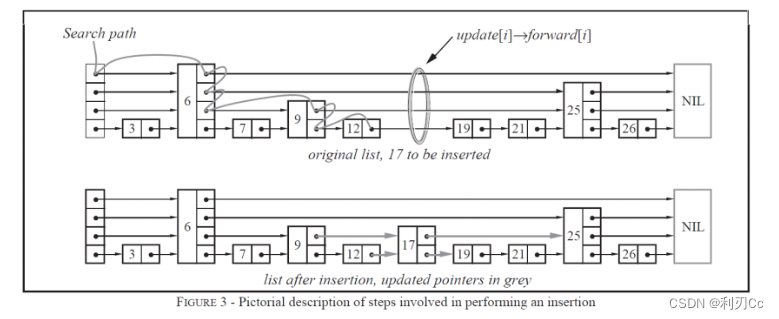
​ 上图中插入 17 这个元素，其实就相当于是放了一堵墙，将 9 和 12 两个元素的指针挡住了，接到了 17 上面，这其实是不影响这些节点的，所以插入过程对其他节点是很稳定的！

​ ♻️ 其中最底层的链表，即包含了所有元素节点的链表是L1层，或称基础层，基础层包括所有的元素。除此以外的所有链表层都称为跳跃层。

3、跳表的搜索方式

​ 我们先来看一个有序链表，如下图（最左侧的灰色节点表示一个空的头结点）：

​ 在这样一个链表中，如果我们要查找某个数据，那么需要从头开始逐个进行比较，直到找到包含数据的那个节点，或者找到第一个比给定数据大的节点为止（没找到）。也就是说，时间复杂度为O(n)。同样，当我们要插入新数据的时候，也要经历同样的查找过程，从而确定插入位置。

​ 假如我们每相邻两个节点增加一个指针，让指针指向下下个节点，如下图：

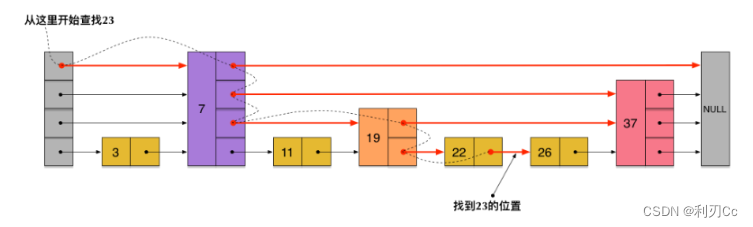
​ 这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半（上图中是7, 19, 26）。现在当我们想查找数据的时候，可以 先沿着这个新链表进行查找，当碰到比待查数据大的节点时，再回到原来的链表中进行查找（也就是向下走）。比如，我们想查找 23，查找的路径是沿着下图中标红的指针所指向的方向进行的：

• 23首先和7比较，再和19比较，比它们都大，继续向右比较。
• 但23和26比较的时候，比26要小，因此要向下走，与22比较。
• 23比22要大，继续向右和26比较。23比26小，说明待查数据23在原链表中不存在，而且它的插入位置应该在22和26之间。

后面若增加了高度，也是一样的遍历方法！

Ⅲ. skiplist的算法性能分析

1、理论准备

​ 如果是第一次接触 skiplist，那么一定会产生一个疑问：节点插入时随机出一个层数，仅仅依靠这样一个简单的随机数操作而构建出来的多层链表结构，能保证它有一个良好的查找性能吗？为了回答这个疑问，我们需要分析 skiplist 的统计性能！

​ 在分析之前，我们还需要着重指出的是，执行插入操作时计算随机数的过程，是一个很关键的过程，它对 skiplist 的统计特性有着很重要的影响。这并不是一个普通的服从均匀分布的随机数，它的计算过程如下：

• 首先，每个节点肯定都有第一层指针。
• 如果一个节点有第 i 层 (i>=1) 指针（即节点已经在第1层到第i层链表中），那么它有第 (i + 1) 层指针的概率为 p。
• 节点最大的层数不允许超过一个最大值，记为 MaxLevel。

这个计算随机层数的伪代码如下所示：

​ randomLevel() 的伪代码中包含两个参数，一个是 p，一个是 MaxLevel。在 Redis 的 skiplist 实现中，这两个参数的取值为：

p = 1/4
MaxLevel = 32

2、性能分析（了解即可，主要记结论）

​ 根据前面 randomLevel() 的伪码，我们很容易看出，产生越高的节点层数，概率是越低的。定量的分析如下：

​ 因此，一个节点的平均层数（也即包含的平均指针数目），计算如下：

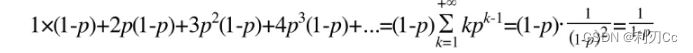
现在很容易计算出：

• 当 p=1/2 时，每个节点所包含的平均指针数目为2；
• 当 p=1/4 时，每个节点所包含的平均指针数目为1.33。这也是Redis里的skiplist实现在空间上的开销。

也可以看出了，我们 取的概率越小，那么产生越高节点的层数的几率就越小！可能有点抽象，画个图帮助理解一下：

​ 接下来，为了分析时间复杂度，我们计算一下 skiplist 的平均查找长度。查找长度指的是查找路径上跨越的跳数，而查找过程中的比较次数就等于查找长度加1。以前面图中标出的查找23的查找路径为例，从左上角的头结点开始，一直到结点22，查找长度为6。

​ 我们注意到，每个节点插入的时候，它的层数是由随机函数 randomLevel() 计算出来的，而且随机的计算不依赖于其它节点，每次插入过程都是完全独立的。所以，从统计上来说，一个 skiplist 结构的形成与节点的插入顺序无关。

​ 这样的话，为了计算查找长度，我们可以将查找过程倒过来看，从右下方第1层上最后到达的那个节点开始，沿着查找路径向左向上回溯，类似于爬楼梯的过程。我们假设当回溯到某个节点的时候，它才被插入，这虽然相当于改变了节点的插入顺序，但从统计上不影响整个 skiplist 的形成结构。

​ 现在假设我们从一个 层数i 的 节点x 出发，需要向左向上攀爬 k层。这时我们有两种可能：

• 如果节点 x 有第 (i+1) 层指针，那么我们需要向上走。这种情况概率为p。
• 如果节点 x 没有第 (i+1) 层指针，那么我们需要向左走。这种情况概率为(1-p)。

这两种情形如下图所示：

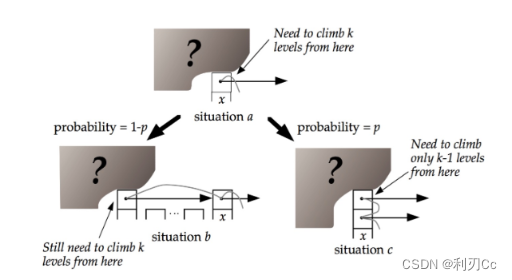
​ 用 C(k) 表示向上攀爬 k 个层级所需要走过的平均查找路径长度（概率期望），那么：

​ 代入，得到一个差分方程并化简：

​ 这个结果的意思是，我们每爬升1个层级，需要在查找路径上走 1/p 步。而我们总共需要攀爬的层级数等于整个 skiplist的总层数-1。

​ 那么接下来我们需要分析一下当skiplist中有n个节点的时候，它的总层数的概率均值是多少。这个问题直观上比较好理解。根据节点的层数随机算法，容易得出：

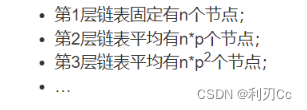
​ 所以，从第1层到最高层，各层链表的平均节点数是一个指数递减的等比数列。容易推算出，总层数的均值为 $lo{g}_{1/p}n$，而最高层的平均节点数为 1/p。

综上，粗略来计算的话，平均查找长度约等于：

• C($lo{g}_{1/p}n-1$) = ($lo{g}_{1/p}n-1$) / p

即，平均时间复杂度为O(log n)。

​ 当然，这里的时间复杂度分析还是比较粗略的。比如，沿着查找路径向左向上回溯的时候，可能先到达左侧头结点，然后沿头结点一路向上；还可能先到达最高层的节点，然后沿着最高层链表一路向左。但这些细节不影响平均时间复杂度的最后结果。另外，这里给出的时间复杂度只是一个概率平均值，但实际上计算一个精细的概率分布也是有可能的。

Ⅳ. skiplist与平衡树、哈希表的比较

​ 如果要实现一个 key-value 结构，需求的功能有插入、查找、迭代、修改，那么首先Hash表就不是很适合了，因为哈希表迭代的时间复杂度比较高；而红黑树的插入很可能会涉及多个结点的旋转、变色操作，因此需要在外层加锁，这无形中降低了它可能的并发度。而 skiplist 底层是用链表实现的，可以实现为 无锁，同时它还有着不错的性能（单线程下只比红黑树略慢），非常适合用来实现我们需求的那种 key-value 结构。

​ 下列是它们的优缺点总结：

• skiplist 和各种平衡树（如AVL、红黑树等）的元素都是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点。
• 在 范围查找的时候，平衡树比 skiplist 操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在 skiplist 上进行范围查找就非常简单，只需要在找到小值之后，对第一层链表进行若干步的遍历就可以实现。
• 平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，且性能会下降，而 skiplist 的插入和删除只需要修改相邻节点的指针，操作简单又快速。
• 从内存占用上来说，skiplist 比 平衡树 更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而 skiplist 每个节点包含的指针数目平均为 1/(1-p)，具体取决于参数p的大小。如果像 Redis 里的实现一样，取 p=1/4，那么平均每个节点包含 1.33 个指针，比平衡树更有优势。
• 查找单个key，skiplist 和平衡树的时间复杂度都为O(log n)，大体相当；而 哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。所以我们平常使用的各种 Map 或 dictionary 结构，大都是基于哈希表实现的。
• 从算法实现难度上来比较，skiplist 比 平衡树 要简单得多。

Ⅴ. skiplist的实现

设计跳表

1、节点的搭建

​ 首先，设计 skiplist 最重要的就是选择用什么数据结构来存储。

​ 在 SkiplistNode 中当然还是比较明显的，因为 skiplist 是基于链表产生，那么我们肯定得**用到链表的结构；除此之外，为了实现多层高度的节点，我们可以用数组，数组中存放的是下一个节点的指针，数组的长度就是节点的高度！**

​ 而 Skiplist 中我们设计一个头节点 _head，头节点内数组的高度就是整个 skiplist 的最大高度，这个需要实时变化的！并且用一个变量 _maxLevel 来代表我们可以达到的最大高度，默认为 32。

struct SkiplistNode
{
    int _val; // 节点的值
    vector<SkiplistNode*> _nextV; // 存储下一个节点的数组

    SkiplistNode(int val, int level)
        :_val(val), _nextV(level, nullptr)
    {}
};

class Skiplist 
{
    typedef SkiplistNode Node;
public:
    Skiplist() 
    {
        _head = new Node(-1, 1); // 默认初始值为-1，高度为1
    }
    
private:
    Node* _head; // 头节点指针
    int _maxLevel = 32; // 节点的最高层数
    double _p = 0.25; // 生成高一层的概率
};

2、生成概率高度函数RandomLevel()

​ 上面讲到的要生成一个概率高度，其实不难，我们可以用c语言中的随机数函数 rand() 配合我们给的 _p，也可以用C++中一些关于随机数的库，可以用其正态分布或者一些随机数函数等 ，不过经过测试，当数据量大的时候，C++中随机数的函数会更加接近概率；而数据量小的时候，两者区别是不大，且c语言的随机数函数占用内存比较小！

​ 下面两种都给出实现：

// c语言版本
int RandomLevel()
{
    int level = 1;
    // rand()的范围在[0, RAND_MAX]之间
    while(rand() <= RAND_MAX*_p && level < _maxLevel)
    {
        level++;
    }
    return level;
}

// c++版本
int RandomLevel()
{
    static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());
	static std::uniform_real_distribution<double> distribution(0.0, 1.0);
    
    int level = 1;
    while (distribution(generator) <= _p && level < _maxLevel)
    {
        level++;
    }
    return level;
}

3、查找函数search()

我们已经在上面讲过了跳表的搜索方式了，其实就是从头节点的最上方（也就是头节点数组的尾部）开始与下一个节点比较，这里列出比较的细节：

• 若节点数组该位置 _nextV[level] 为空，说明该位置的下一个节点为空，则**直接向下跳**
• 若节点数组该位置 _nextV[level] 不为空，则与下一个节点进行比较：
  • 若比下一个节点的值小，则向下跳
  • 若比下一个节点的值大，则向右跳
  • 若和下一个节点的值相等，则返回 true 即可
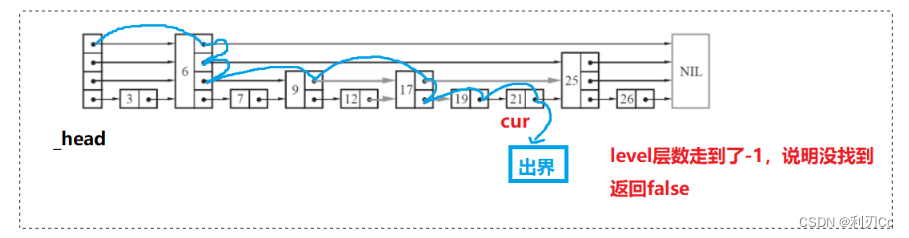
• 循环查找，直到 level 为 -1，也就是出界了则结束，说明没找到节点，返回false（level 代表目前所在的层数）

🔴 要注意的是我们查找遍历的时候，肯定也是**需要一个 cur 指针来指向当前走到的节点**的！

​ 以下图为例，查找 21 的过程如下：

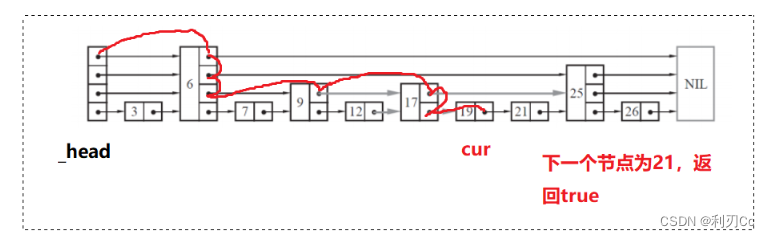
​ 若是查找 23，那么过程如下：

bool search(int target) 
{
    Node* cur = _head;
    int level = _head->_nextV.size() - 1; // 目前的最高层数在数组中的位置
    while(level >= 0)
    {
        // 1、该位置的下一个节点不为空，且下一个节点的值小于target，则向右跳
        // 2、该位置为空或者下一个节点的值大于target，则向下跳
        // 3、剩下的情况就是找到了，返回true即可
        if(cur->_nextV[level] != nullptr && target > cur->_nextV[level]->_val)
        {
            cur = cur->_nextV[level];
        }
        else if(cur->_nextV[level] == nullptr || target < cur->_nextV[level]->_val)
        {
            // 向下跳就是将level--
            level--;
        }
        else
        {
            // 找到了返回true
            return true;
        }
    }
    return false;
}

4、插入函数add()

​ 插入就稍微比较复杂了一点，因为我们不只是要插入节点，我们还要将节点的前后指针链接起来，而关键的解题点就是 要找到插入位置的每一层的前一个节点，以下是思路：

1. 与 search() 一样，遍历查找要插入的位置，也就是 level < 0 时出界时候 cur 指针的位置
2. 在遍历时候的一个关键细节，就是 将每次比我们要插入的值 num 小或下一个节点为空的位置记录下来保存到一个新的节点数组 _preV ，因为既然它比 num 小，那么它这个层数的指针就会被 num 挡住（除非新插入节点的高度小于该位置的高度）。不断循环遍历直到找到了要插入的位置
3. 找到插入的位置之后，先利用 RandomLevel() 函数产生概率高度，然后构造新节点 newnode
4. 将 _preV 中的前驱节点与 newnode 节点 按层数将它们的前后链接起来 ，为什么说是按层数链接起来呢？因为每一层只会链接一个节点，所以有几层就会链接多少次，且是天然按照顺序来的！

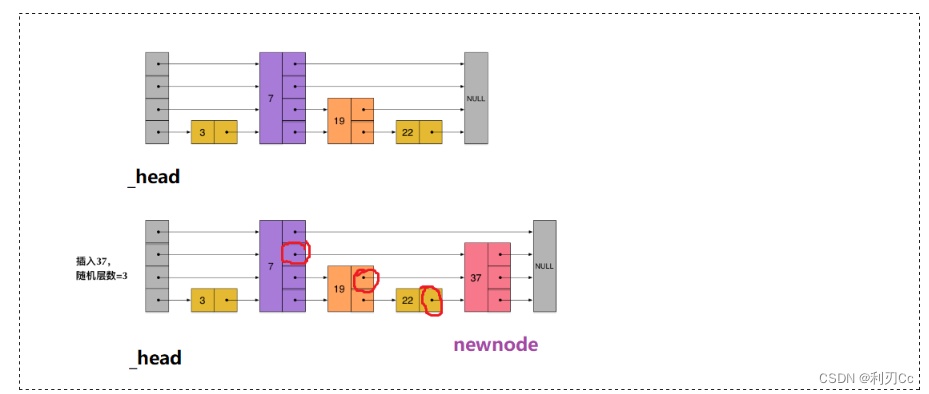
​ 如上图中红圈圈出来的就是这些比 37 小的位置，记录到 _preV 中！

​ 因为下面的删除函数erase()，也需要进行遍历，所以我们将其中的遍历记录前驱节点的操作独立出来成一个函数 FindPrevNode()。

vector<Node*> FindPrevNode(int num)
{
    Node* cur = _head;
    int level = _head->_nextV.size() - 1; // 目前的最高层数在数组中的位置
    vector<Node*> _preV(level+1, nullptr); // 用于记录前驱节点，注意高度是level+1

    while(level >= 0)
    {
        // 与search()类似，只不过找到比num小的时候记录一下这些位置
        if(cur->_nextV[level] != nullptr && num > cur->_nextV[level]->_val)
        {
            cur = cur->_nextV[level];
        }
        else if(cur->_nextV[level] == nullptr || num <= cur->_nextV[level]->_val)
        {
            // 将该位置的指针记录到_preV中
            _preV[level] = cur;

            // 向下跳就是将level--
            level--;
        }
    }
    return _preV;
}

void add(int num) 
{
    vector<Node*> preV = FindPrevNode(num);

    // 找到了插入位置后，构造新节点
    int n = RandomLevel();
    Node* newnode = new Node(num, n);

    // 判断一下新节点的高度是否大于目前高度，会的话更新头节点的高度
    if(n > _head->_nextV.size())
    {
        _head->_nextV.resize(n, nullptr);
        preV.resize(n, _head);
    }

    // 将前后指针链接起来
    for(size_t i = 0; i < n; ++i)       
    {
        newnode->_next[i] = preV[i]->_nextV[i];
        preV[i]->_nextV[i] = newnode;
    }
}

5、删除函数erase()

​ 删除的大体思路也是不难的，最主要的也是得找出要删除节点的前驱节点集合，将前驱节点指向删除节点的后继节点，还要注意的判断一下删除完这个节点后该高度是否整体变低了，是的话要调整一下头节点的高度（因为头节点的高度代表整个跳表的高度）！

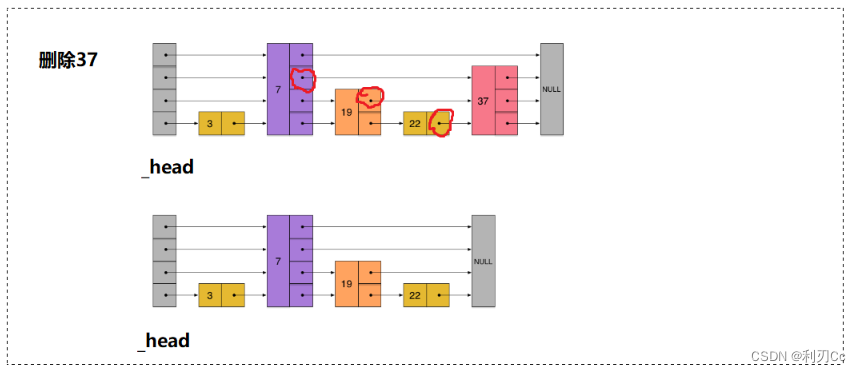
1. 遍历跳表 找到要删除的节点，遍历的 同时将那些值比 num 小的节点记录到数组 preV 中，过程和插入函数是类似的，直接利用FindPrevNode() 函数实现即可
2. 将要删除节点的前驱节点集合与删除节点的后继节点链接起来
3. 遍历头节点判断一下是否删除节点后整体高度变低，只需要判断 _head->_nextv[level] 是否为空，是的话说明变低了，则降低高度，直到不为空。

bool erase(int num) 
{
    // 找到前驱节点集合
    vector<Node*> preV = FindPrevNode(num);

    // 此时最底层的前驱节点的下一个节点就是要删除的节点
    Node* del = preV[0]->_nextV[0];

    // 判断一下删除节点del是否为空或者值是否为num，不是则直接返回false
    if(del == nullptr || del->_val != num)
    {
        return false;
    }
    else
    {
        // 将前驱节点链接del的后继节点
        for(size_t i = 0; i < del->_nextV.size(); ++i)
            preV[i]->_nextV[i] = del->_nextV[i];

        // 判断一下是否需要降低整体高度
        int i = _head->_nextV.size() - 1;
        while (i >= 0)
        {
            if (_head->_nextV[i] == nullptr)
                --i;
            else
                break;
        }
        _head->_nextV.resize(i + 1);

        delete del;
        return true;
    }
}

Ⅵ. 关于Redis中的一些拓展知识

​ 在 Redis 中，skiplist 被用于实现暴露给外部的一个数据结构：sorted set。准确地说，sorted set 底层不仅仅使用了 skiplist，还使用了 ziplist 和 dict。

• 当数据较少时，sorted set是由一个ziplist来实现的。
• 当数据多的时候，sorted set是由一个dict + 一个skiplist来实现的。简单来讲，dict用来查询数据到分数的对应关系，而skiplist用来根据分数查询数据（可能是范围查找）。

🈂️ Redis为什么用skiplist而不用平衡树？

There are a few reasons:

1. They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

2. A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

3. They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

原因如下：

1） 它们不太需要记忆。这基本上取决于你。改变关于节点具有给定数量级别的概率的参数将使其比btrees的 内存占用更少。

2） 排序集通常是许多ZRANGE或ZREVRANGE操作的目标，也就是说，将跳表作为链表遍历。使用此操作，跳表的缓存位置至少与其他类型的平衡树一样好。

3） 跳表更易于实现、调试 等。