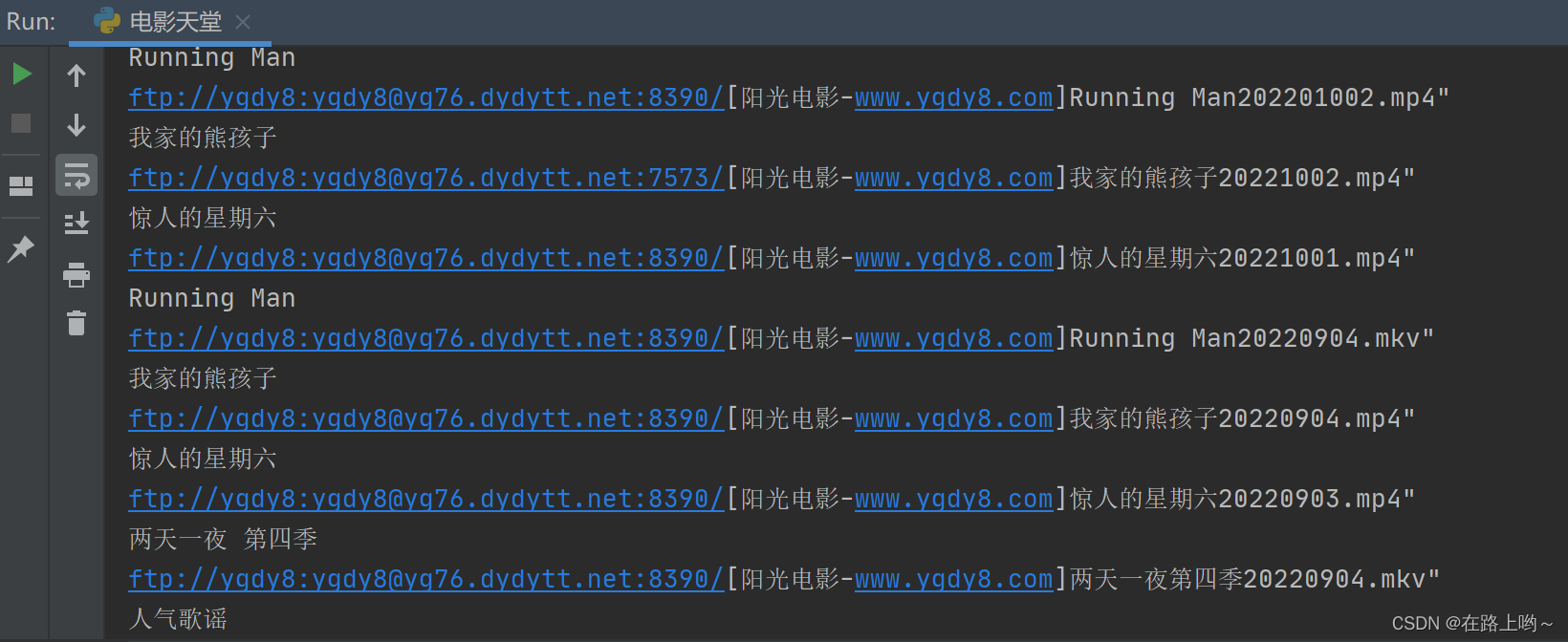
提取 最新综艺资源推荐 的电影名字和下载链接
"""
1、先从首页网址定位
2、在定位的的位置找到子页面的链接地址
3、请求子页面的链接地址,拿到我们想要的下载地址
"""
"""1、定位到最新综艺资源推荐"""
import requests
import re
# requests.urllib3.disable_warnings() # 禁用安全警告
domain = 'https://www.dytt.to/'
resp = requests.get(domain,verify=False) # verify=False 去掉安全验证
resp.encoding='gb2312'
# print(resp.text)
# 拿到ul里面的li
obj1=re.compile(r'最新综艺资源推荐.*?<ul>(?P<ul>.*?)</ul>',re.S)
obj2 = re.compile(r"<a href='(?P<href>.*?)'>.*?</a>",re.S)
obj3 = re.compile(r'<meta name=description content="(?P<movie>.*?)免费下载,迅雷下载">.*?'
r'<td style="WORD-WRAP: break-word" bgcolor="#fdfddf"><a href="(?P<download>.*?)>',re.S)
result1=obj1.finditer(resp.text)
child_href_list = []
for it in result1:
ul=it.group('ul')
# print(ul)
"""提取子页面链接:"""
result2=obj2.finditer(ul)
for itt in result2:
"""拼接子页面的Url地址: 域名+ 子页面地址"""
child_href = domain + itt.group("href").strip("/") # .strip("/") 去掉前面的“/"
# print(child_href)
child_href_list.append(child_href) # 把子页面吗链接保存起来
"""2、提取子页面内容"""
for href in child_href_list:
child_resp=requests.get(href,verify=False)
child_resp.encoding='gb2312'
# print(child_resp.text)
result3 = obj3.search(child_resp.text)
print(result3.group("movie"))
print(result3.group("download"))
# break # 测试用