什么是连通分量
无向图 G 的最大连通子图称为 G 的连通分量。
注：这里的最大连通子图的含义为：此图为 G 的连通子图，将 G 的任意一个点加到盖子图中之后，此子图将不再连通。
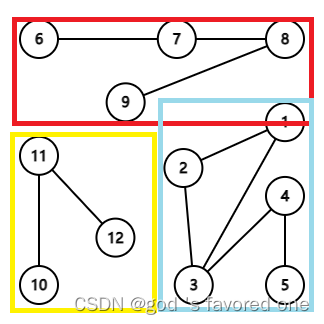比如这一张图中，很显然，我用三种颜色圈起来的部分都是原图的连通分量。（其实可以十分形象的理解成每一个连通分量都是一个连通块）回想到以前的“亲戚”一题，就是让我们去求在这个无向图中，询问的两个点是不是在同一个连通分量中。值得注意的一点，一个连通图的连通分量就是他本身。
关于有向图图的连通的一些概念
假如在一个有向图中对于每一对点 vi,vj 都存在 vi->vj 的路径和 vj->vi 的路径（值得注意的是，这里是存在一条路径，而不是存在一条边），那么就称之为强连通图。
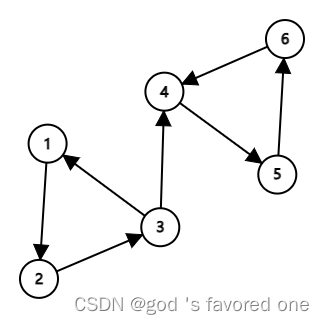
很显然，这一张图就是一个强连通图。有向图 G 的子图是强连通图，那么称该图为强连通子图。
显然，在上图中 (1, 2, 3) 和 (4, 5, 6) 都是强连通子图。
有向图 G 的最大强连通子图则称为 G 的强连通分量（这里的“最大”和之前是一个意思），显然，在上图中，最大强连通子图为图本身。
关于无向图的连通的一些概念
双连通图：在任意两个点之间都存在至少 2 条不相交（可以理解为不重叠，我原本理解了半天）路径的图。
割点：如果删掉点 v 和与 v 相关联的边，那么得到新图至少有两个双连通分量， 那么称点 v 为割点。
桥：如果无向图中的桥后（桥是一条边），得到的新图包含两个连通分量。
双连通图：不包含割点的无向连通图。
双连通分量：无向连通图的最大双连通子图。
点双连通分量：通过找割点获得的双连通分量。
边双连通分量：通过找桥获得的双连通分量。
为了举例子，在这里我继续使用上面的那一张图（换为无向）。
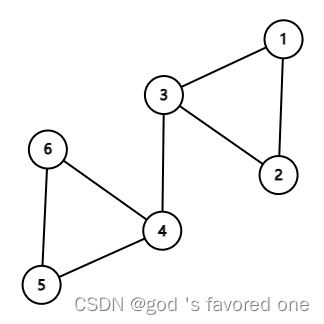
在图中，桥只有 (3, 4) 一条边，而割点只有 3、4 两个点。
Tarjan 算法
原本还有一个 kosaraju 算法，因为没有什么用，在这里就不专门介绍了。
这里我们用 dfn[i] 表示编号为 i 的节点在 dfs 的过程中的遍历顺序，就是一个 dfs 序。（也可以叫时间戳）
用 low[i] 表示 i 节点及其下方节点所能到达的开始时间最早的节点的开始时间。（初始时 low[i] = dfn[i]）
这里有 1 个性质：因为在 dfs 的过程中会形成一棵搜索树，所以在越上面的节点显然 dfn 就会越小。
如果发现一个点有边连到了搜索树中的自己的祖宗节点，那么就更新其 low 的值。
关于 low 值与 dfn 值
1、如果一个节点的 low 值小于 dfn 值，那么就说明它或者它的子孙节点有边连到自己上方的节点。
2、如果一个节点的 low 值等于 dfn 值，则说明其下方的节点不能走到其上方节点，那么该节点就是一个强连通分量在搜索树中的根。
3、但是 u 的子孙节点就未必和 u 处于同一个强连通分量，用栈存储即可（具体看代码）。
代码实现：
void tarjan(int u)
{
dfn[u] = low[u] = ++ dn; // 将 dfn 和 low 都赋值为编号 dn
sta[ ++ tt] = u, vis[u] = 1, st1[u] = 1;
// 将当前点 u 加入栈中，标记为访问过，已经入栈
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!vis[j]) // 如果这个点还没有被访问过，就访问
{
tarjan(j); // 继续搜这个点的儿子节点
low[u] = min(low[u], low[j]);
// 更新这个点的 low 值为 low[u] 和 low[j] 的较小值
}
else if (st1[j]) // 如果这个点已经在栈中了
low[u] = min(low[u], dfn[j]);
// 那么就把这个点和这个子节点的 dfn 取最小值
}
int t;
if (dfn[u] == low[u])
// dfn[u] == low[u] 表示 u 是一个强连通分量的跟根
{
scc ++ ;
// 统计连通分量的个数
do
{
t = sta[tt -- ];
st1[t] = 0;
// 取出，标记为不在栈中
cout << t << ' ';
}while (u != t);
cout << '\n';
// 输出最大强连通分量
}
}当然，要求整张图的最大连通分量，就要在主函数中这样调用它：
for (int i = 1; i <= n; i ++ )
if (!dfn[i]) tarjan(i);这样就可以求出所有的最大连通分量了！
用 Tarjan 算法求割点和桥
割点：如果一个点为 割点，那么当且仅当满足性质 (1) 或 (2)。
(1)：u 为树根，且有超过一个子树。
(2)：u 不为树根，且满足存在 (u, v) 为树枝边，使得 dfn(u) <= low(v)。
桥：如果一条无向边 (u, v) 是桥，当且仅当 (u, v) 为树枝边，且满足 dfn[u] < low[v]（前提是这条边不存在重边，不然删掉之后还是有边）。
关于割点，可以参考这个代码：
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N = 200010, M = N * 2, mod = 998244353;
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
int n, m, root;
int dn, dfn[N], low[N], cnt, tt, sta[N];
int h[N], e[M], ne[M], w[M], idx, scc;
bool st[N], st1[N], vis[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u)
{
int son = 0;
dfn[u] = low[u] = ++ dn;
sta[ ++ tt] = u, vis[u] = 1, st1[u] = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!vis[j])
{
tarjan(j), son ++ ;
low[u] = min(low[u], low[j]);
/*
if (dfn[u] < low[v])
cout << u << ' ' << v << '\n';
输出桥
*/
if (low[j] >= dfn[u] && u != root)
cnt += !st[u], st[u] = 1;
}
else if (st1[j])
low[u] = min(low[u], dfn[j]);
}
if (son >= 2 && u == root)
cnt += !st[u], st[u] = 1;
int t;
/*
if (dfn[u] == low[u])
{
scc ++ ;
do
{
t = sta[tt -- ];
st1[t] = 0;
cout << t << ' '
}while (u != t)
cout << '\n';
}
输出最大强连通分量
*/
}
int main()
{
memset (h, -1, sizeof h);
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= m; i ++ )
{
int u, v;
cin >> u >> v;
add (u, v), add(v, u);
}
for (int i = 1; i <= n; i ++ )
if (!dfn[i]) root = i, tarjan(i);
cout << cnt << '\n';
for (int i = 1; i <= n; i ++ )
if (st[i]) cout << i << ' ';
return 0;
}这个是洛谷 P3388 的代码，桥的代码和最大连通分量的代码也在其中。
关于 Tarjan 缩点的方法
这里草草的说一下，其实缩点就在 Tarjan 求强连通分量的时候用一个 id 数组和 cnt 数组，存一下每一个点在哪一个强连通分量中和强连通分量的大小，就可以了，实现如下：
if (dfn[u] == low[u])
{
scc ++ ;
do
{
t = sta[tt -- ];
st1[t] = 0;
id[t] = scc, cnt[scc] ++ ;
// cout << t << ' ';
}while (u != t)
// cout << '\n';
}关于 Tarjan 算法的一些介绍就说到这里了，下次再见 ~~。
