1、原理介绍

一簇点云的最小外包矩形（Minimum Bounding Rectangle，MBR），是指用一个矩形将该簇点云框起来，所有点云数据在矩形框内。如下图所示为一个矩形框刚好将点云数据全部包围。

下面给出一种基于最大重叠度的最小外包矩形，该方法依据任意相邻点计算得到多个矩形，选择轮廓点与该矩形重叠度最大的矩形作为最小外包矩形。具体步骤如下：

（1）对点云进行边缘点提取，并对边缘点进行排序，得到有序边缘点；

（2）对于每个轮廓点，选择与其相邻的下一个近邻点构成一条直线，以该直线与其垂直的直线确定最小外包矩形方向，计算得到一个最小外包矩形。

（3）选择下一个轮廓点，重复步骤（2）即可得到下一个最小外包矩形。遍历所有的轮廓点即可得到一些列最小外包矩形。

（4）由上述获取的最小外包矩形，计算边缘点到矩形四条边的距离，若到四条边的垂直距离均大于设定阈值，则为不重叠点，否则为重叠点。

如下图中p点，计算其到四条边的距离示意图。

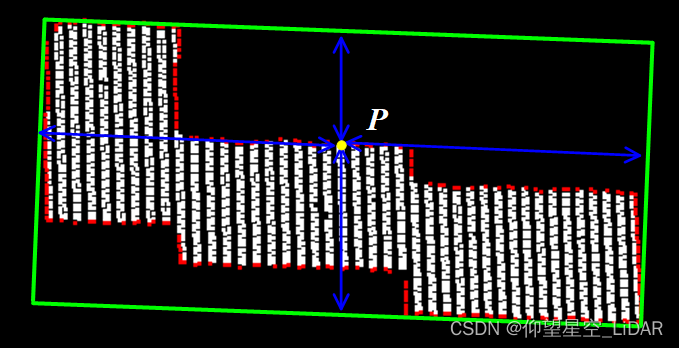
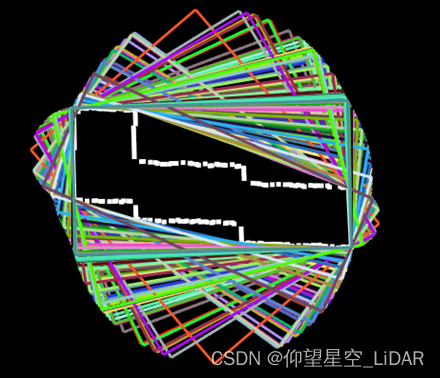
任意相邻点确定的最小外包矩形，如下图所示。从中选择重叠度最大的外包矩形，即可得到理想的外包矩形。

2、测试及结果

根据上述原理，基于PCL、C++进行实现。提取的边缘点、所有轮廓线、最大重叠度矩形结果如下图所示。

部分计算代码如下：

//计算重叠度
double RateOverlapBoundarySides(vector<pcl::PointXYZ> boundarypoints, Rect onerectangle, double DsThres)
{

	LinePara Line1, Line2, Line3, Line4;
	Line1 = CalculateLine(onerectangle.leftbottom, onerectangle.leftup);
	Line2 = CalculateLine(onerectangle.leftup, onerectangle.rightup);
	Line3 = CalculateLine(onerectangle.rightup, onerectangle.rightbottom);
	Line4 = CalculateLine(onerectangle.leftbottom, onerectangle.rightbottom);

	vector<pcl::PointXYZ>inliers;//重叠点与非重叠点
	for (int i = 0; i < boundarypoints.size(); i++)
	{
		vector<double> Dsvec;
		Dsvec.push_back(Point2Dline(Line1, boundarypoints[i]));
		Dsvec.push_back(Point2Dline(Line2, boundarypoints[i]));
		Dsvec.push_back(Point2Dline(Line3, boundarypoints[i]));
		Dsvec.push_back(Point2Dline(Line4, boundarypoints[i]));
		//选择最小值
		double minds = getMin_vector(Dsvec);
		if (minds < DsThres)
		{
			inliers.push_back(boundarypoints[i]);
		}
	}
	double result = (float)inliers.size() / boundarypoints.size();
	return result;
}

//获取重叠度最大的矩形
// DsThres 距离阈值，确定该点是否为重叠点
Rect MaxOverlapBoundaryRec(vector<pcl::PointXYZ> boundarypoints, vector<Rect> onerectangle, double DsThres)
{
	
	vector<double> ratevec;//百分比
	for (int i = 0; i < onerectangle.size(); i++)
	{
		ratevec.push_back(RateOverlapBoundarySides(boundarypoints, onerectangle[i], DsThres));
	}

	double maxindex = GetIndexOfMax(ratevec);
	return onerectangle[maxindex];

}

该程序包括三个测试main函数，分别为测试边缘点检测、所有矩形可视化显示、最小外包矩形。结果如下：