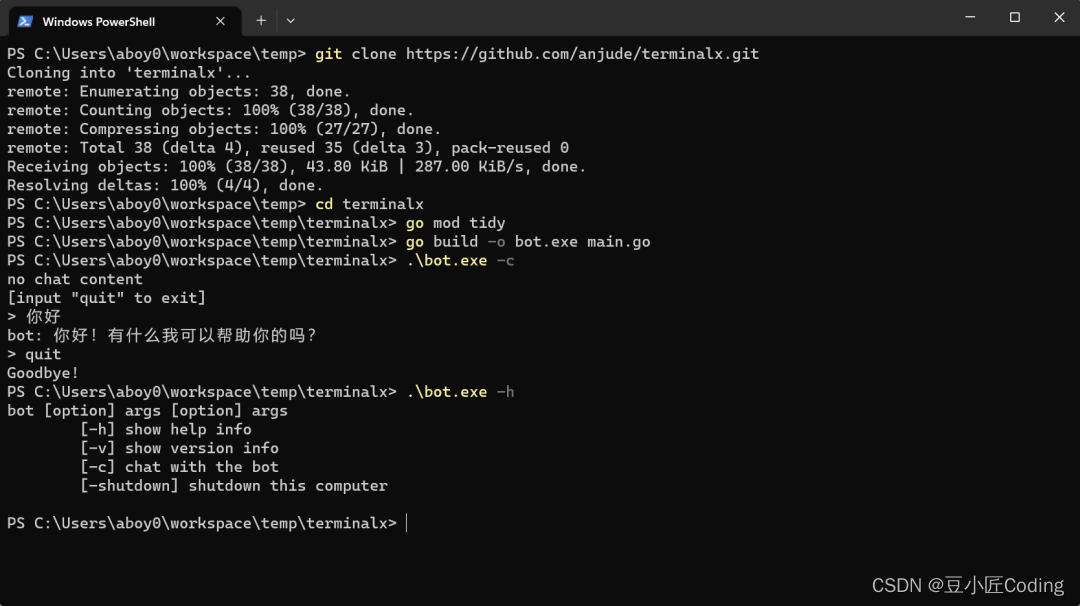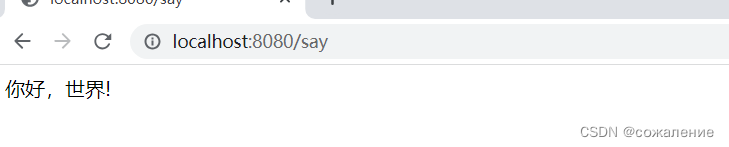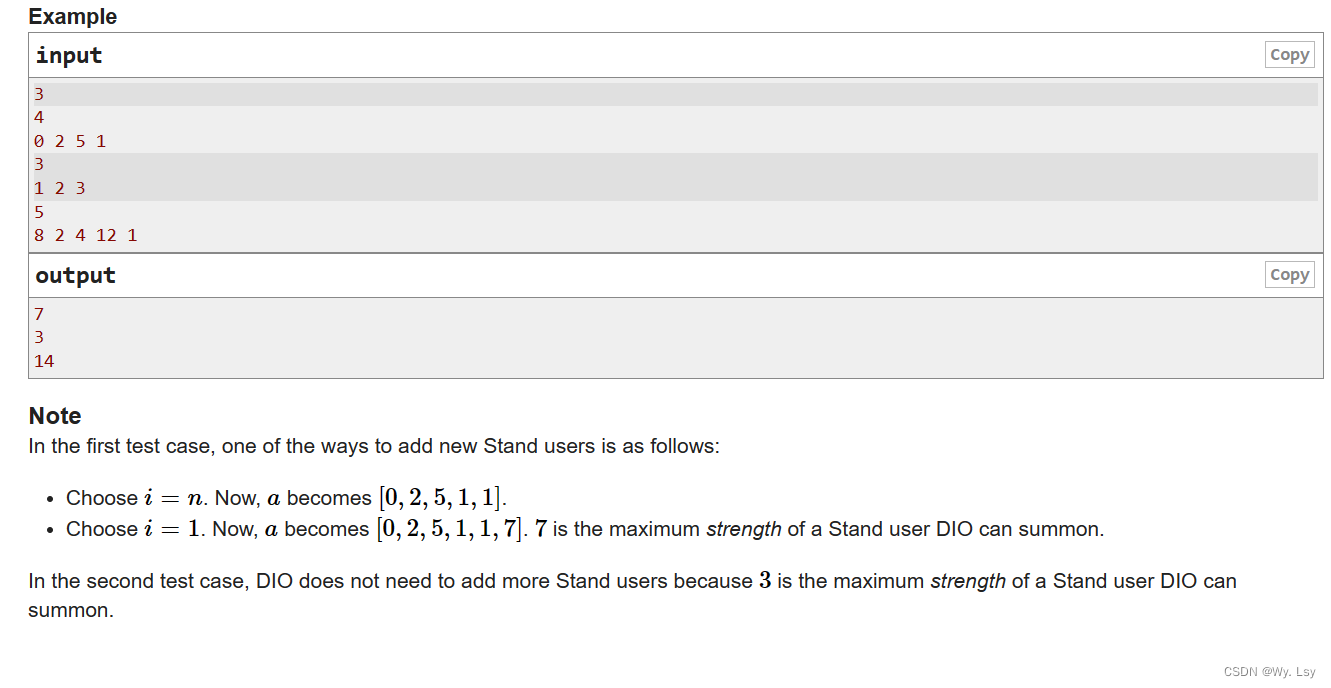
分析：

        添加新元素的操作可以理解为添加任意一段以n结尾的异或和，当原数组总异或和与新加的元素进行异或又可以得到剩余的前缀的异或和，假设新加的元素的值是i到n的异或和x，那么总异或和sum=pre^x，所以sum^x==pre，所以通过操作可以得出任意一段的区间异或和，可以通过前缀和来处理进而查询区间异或和，但是查找区间异或和需要O(n*n）的时间复杂度，会超时，ai的范围很小，所以所有的异或和范围都会在0~2^8之间，可以直接遍历前缀数组，然后第二层循环改为查找1~2^8之间是否出现过某一个异或和的值，再和当前遍历的前缀和进行异或操作，就可以得到部分区间异或和。

代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef pair<int,int> pii;

int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

	int _;
	cin>>_;
	while(_--)
	{
		int n;
		cin>>n;
		vector<int> a(n+1);
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
			a[i]^=a[i-1];
		}
		map<int,int> m;
		m[0]=1;
		int ans=0;
		for(int i=1;i<=n;i++)
		{
			for(int j=0;j<256;j++)
			{
				if(m[j]) ans=max(ans,j^a[i]);
			}
			m[a[i]]=1;
		}
		cout<<ans<<'\n';
	}
}