文章目录
- PageRank算法工作原理
- 简化版本
- 完整版本
- graphs分析
- graphs代码 [^4]
- 结语
PageRank算法工作原理
算法原理1
简化版本
若页面B,C,D…N都有链接到页面A上,则页面A的PageRank值如下:
P
R
(
A
)
=
(
P
R
(
B
)
L
(
B
)
+
P
R
(
C
)
L
(
C
)
+
P
R
(
D
)
L
(
D
)
+
.
.
.
+
P
R
(
N
)
L
(
N
)
)
d
+
1
−
d
N
PR(A)=(\frac{PR(B)}{L(B)}+\frac{PR(C)}{L(C)}+\frac{PR(D)}{L(D)}+...+\frac{PR(N)}{L(N)})d+\frac{1-d}{N}
PR(A)=(L(B)PR(B)+L(C)PR(C)+L(D)PR(D)+...+L(N)PR(N))d+N1−d 2
完整版本
区别简化版本完整版本引入了阻尼系数
d
d
d的概念(任意时刻,用户访问到某页面后继续访问下一个页面的概率,相对应的
1
−
d
1-d
1−d则是用户停止点击,随机浏览新网页的概率。并且开始声明的
d
=
0.85
d=0.85
d=0.85故完整公式如下:
P
R
(
p
i
)
=
1
−
d
N
+
d
∑
p
j
∈
M
(
p
j
)
P
R
(
p
j
)
L
(
p
j
)
PR(p_i)=\frac{1-d}{N}+d\sum_{p_j\in M(p_j)}\frac{PR(p_j)}{L(p_j)}
PR(pi)=N1−d+d∑pj∈M(pj)L(pj)PR(pj) 3
graphs分析
结构图
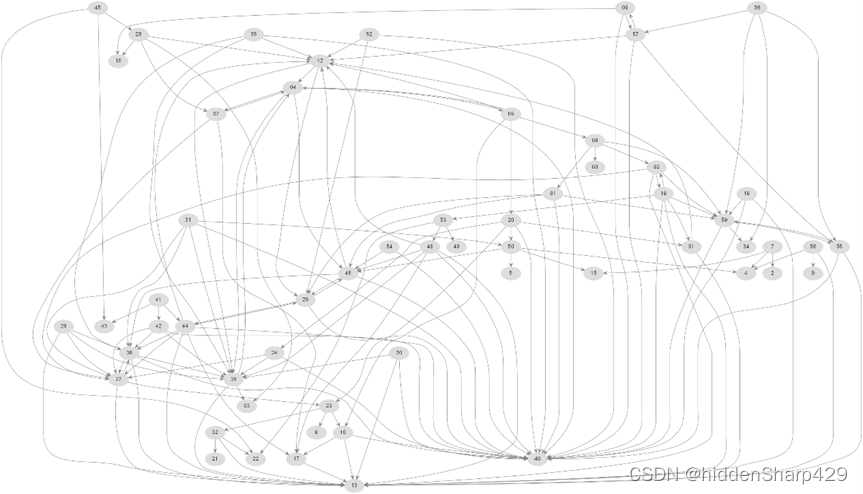
柱状图
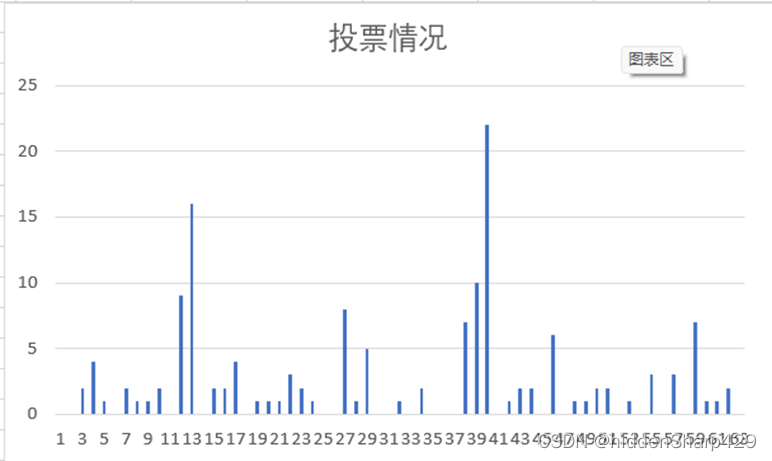
graphs代码 4
digraph G {
// 设置图的布局引擎为dot
layout=dot;
// 边的样式
edge [color="#888888", arrowhead="vee"];
// 节点的样式
node [shape="ellipse", style="filled", fontname="Arial", color="#DDDDDD", fontcolor="#333333"];
// 节点之间的连接
12 -> {04 29 39};
19 -> {13 40 51 53 59 62};
20 -> {23 24 40 50 51};
26 -> {13 27 38 39};
29 -> {40 44 46};
57 -> {09 12 40 55};
45 -> {43 22 28};
08 -> {59 60 61 62};
54 -> {40 46};
09 -> {10 40 57};
23 -> {16 8 32};
38 -> {13 27 39 40};
39 -> {03 04 13};
41 -> {42 43 44};
42 -> {27 38 39 40};
46 -> {12 29 38 40};
50 -> {4 5 15 46};
51 -> {12 13};
52 -> {12 29 40};
55 -> {13 40 59};
59 -> {34 40 55};
61 -> {29 40 46 59};
48 -> {12 13 17 39 40 46};
35 -> {12 38 39 40};
24 -> {27 39 40};
31 -> {27 38 39 40 50};
36 -> {34 55 57 59};
32 -> {13 21 22};
18 -> {13 40 59};
07 -> {04 17 27};
62 -> {13 19 27 59};
16 -> {13 17 40};
44 -> {12 13 17 27 29 38 40};
7 -> {2 4 15};
53 -> {49 22 48};
56 -> {4 9 13};
05 -> {04 08 12 16 20};
04 -> {05 07 40 46 39};
27 -> {13 23 38};
30 -> {13 39 40};
28 -> {03 07 10 12};
17 -> {13};
}
结语
如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!
源于PageRank-wiki ↩︎
L ( x ) L(x) L(x)是每个页面的连出总数, d d d为修正系数,由于“没有向外链接的网页”可能存在,所以赋给每个页面一个最小值 ( 1 − d ) N \frac{(1-d)}{N} N(1−d) ↩︎
p 1 , p 2 . . . . p n p_1,p_2....p_n p1,p2....pn是目标页面, M ( p i ) M(p_i) M(pi)是链入𝑝𝑖页面的集合, L ( p j ) L(p_j) L(pj)是页面 p j p_j pj链出页面的数量, N N N是集合中所有页面的数量 ↩︎
Graphviz操作参考文章 ↩︎