文章目录

前言
一、使用oommf的avf2odt命令行程序获取斯格明子中心位置的示例
二、当磁体系的单个xy平面层仅有一个斯格明子的情况
- 1.读取所有磁化文件中的指定磁化分量
- 2.筛选出每一个xy平面层中位于磁化分量阈值范围内的单元格
- 3.计算组成磁结构的所有单元格的平均坐标和平均距离
三、当磁体系的单个xy平面层存在多个斯格明子和磁畴壁共存的情况
- 1.递归查找处于磁化分量阈值范围内的紧邻的单元格并分离成不重叠的磁结构
- 2.根据每一个磁结构的单元格排布规律来区分出斯格明子和磁畴壁
四、使用OpenCV库函数来识别“圆”特征
五、测试验证
总结

泥上偶然留指爪，鸿飞那复计东西。——苏轼《和子由渑池怀旧》

前言

近来想做一个与磁斯格明子相关的内容，但苦于没有找到有关获取磁化文件中斯格明子的中心位置和半径的参考代码，所以只能自己动手丰衣足食了。主要思路是参考oommf官网上识别磁化文件中斯格明子的方法，即遍历单个磁化文件中所有xy平面层中的单元格，再从每一个xy平面层中筛选处于磁化分量阈值范围内即磁畴壁区域中的单元格，最后把位于斯格明子环状畴壁中所有单元格的平均坐标作为斯格明子的中心位置，取中心位置到这些单元格的平均距离作为半径。本文还通过递归查找紧邻单元格的方式来分离出磁体系中存在的多个斯格明子和多个磁畴壁等磁结构，然后根据每一个磁结构的单元格排布规律来判断是否为斯格明子。另外还提供了一种利用OpenCV库函数的方法，将每一个xy平面层的单元格映射为灰度图中的一个像素点，然后用OpenCV库函数去识别“圆”特征，并得到“圆”的中心位置和半径。最后，则是通过复现一篇文章中的部分内容来测试该程序。该程序的源码见文末的下载链接。

######
本文链接：https://blog.csdn.net/qq_43572058/article/details/131617080
CSDN@搬砖工人_0803号
######

一、使用oommf的avf2odt命令行程序获取斯格明子中心位置的示例

参考oommf网页链接，该作者通过使用命令行tclsh oommf.tcl avf2odt -average space -index t ns '$i*0.05' -valfunc xpos nm '$vz>0.5 ? $x*1e9 : 0' -valfunc ypos nm '$vz>0.5 ? $y*1e9 : 0' -valfunc wgt '' '$vz>0.5 ? 1 : 0' -defaultvals 0 -headers collapse -truncate 1 -onefile foo-a.odt skyrmion_example-alpha0.100-Oxs_TimeDriver-Spin-*omf来利用avf2odt程序遍历所有矢量场文件，对每一个矢量场文件遍历其所有单元格，若某一个单元格的z分量的值满足-valfunc参数定义的阈值范围，则将该单元格的坐标放入统计列表，最后根据-average参数来计算输出每一列的值。显然该方法只适用于磁体系的单个平面层中仅有一个斯格明子的情况，一旦有着两个及以上的斯格明子，或者斯格明子和磁畴壁等其他磁结构同时存在的情况下，该方法就不可用了。此外，虽然感觉也可以通过该命令行程序获取斯格明子的半径，但相比于苦思冥想构造命令行，还不如直接写一个程序来计算半径来的简单。

在这里插入图片描述

通过该示例，我们可以大致理解如何从一个磁化文件中（一般我们使用微磁模拟软件只输出磁化分布M(r,t)的文件，所以后文简称为磁化文件）找到斯格明子的中心位置的过程了。对于每一个磁化文件来说，首先要定义一个磁畴壁所处的磁化分量阈值范围（无磁性的单元格的三个磁化分量都为零，所以需要首先排除掉无磁性的单元格，再进行后续的筛选操作），接着遍历该磁化文件中所有的单元格，筛选出处于磁化分量阈值范围内的所有单元格，即找到位于斯格明子的环状畴壁中的单元格，最后对这些单元格的坐标取平均值并作为斯格明子的中心位置。此外，在本文中直接取该中心位置到这些环状畴壁中单元格的平均距离作为斯格明子的半径。

二、当磁体系的单个xy平面层仅有一个斯格明子的情况

1.读取所有磁化文件中的指定磁化分量

关于OVF矢量场文件的格式请查阅笔记01，由于它的标题行是文本格式，而数据行可以是文本格式（text）或者4/8字节的二进制格式（b4/b8），所以这种混合格式的文件并不容易读取。囿于个人coding水平有限导致不知道如何读取这种混合格式的文件，所以只能使用avf2ovf命令行程序非常麻烦耗时的将磁化文件的数据行转化为文本格式，从而让整个磁化文件的格式统一，方便使用numpy库的loadtxt函数读取磁化文件中指定的数据列。当然，在模拟开始前，我们可以在mumax的代码中添加一行语句 OutputFormat = OVF2_TEXT，在oommf的driver类中添加一行语句 vector_field_output_format {text %#.17g}，从而让模拟软件输出的磁化文件的默认格式从二进制格式变成text文本格式。
这里扩展了笔记05中MFA读取磁化文件中指定磁化分量的代码，根据该程序是否第一次读取磁化文件分为单进程读取和多进程读取的方法，将所有磁化文件的所有单元格的指定磁化分量按读取顺序放入一个结果列表m_allFiles返回：

from functools import partial
import numpy as np
import os
from multiprocessing import Pool

##读取一个磁化文件中的某一磁化分量，name：文件名称；colum：读取的矢量分量
def fileload(name,colum):
    colum = int(colum)
    #磁化文件中'#'是注释
    m_oneFile = np.loadtxt(name, dtype = float, encoding='utf-8', comments = '#', usecols = (colum,))
    print("已读取:",name,flush=True)
    return m_oneFile

#该函数的返回值为[array([...]), array([...])...]，列表的一个元素表示保存一个磁化文件的某个分量的浮点型数组
#列表长度为当前文件夹中所有子文件数量
#dirc：存放磁化文件的目录
#start_stage，end_stage：需要的磁化文件的范围
#exportX,exportY,exportZ：选择磁化矢量的那个分量表征斯格明子信息
def readUseOneCore(dirc,start_stage,end_stage,exportX,exportY,exportZ):
    #磁化文件中的第三列表示Z分量
    if exportZ == 1:
        column = '2'
    #磁化文件中的第二列表示Y分量
    elif exportY == 1:
        column = '1'
    #磁化文件中的第一列表示X分量
    else:
        column = '0'

    #定义一个保存磁化文件名称的空列表
    files = []
    #walk函数会以文件夹为单位自顶而下遍历指定文件目录，
    #返回的三个参数分别表示当前文件夹, 当前文件夹中的子文件夹, 当前文件夹中的子文件
    for i,j,k in os.walk(dirc):
        #获取当前文件夹中所有磁化文件，并保存到列表中
        #因此，这里的files是二维列表：files[k[...]]
        files.append(k)
    #将files转化为一维列表
    files = files[0]
    #对列表中的磁化文件进行按名称升序排序
    files.sort()
    files_sort = files[:]
    #创建一个保存磁化文件全路径名称的列表
    files_new = []
    for i in range(start_stage,end_stage):
        files_new.append(dirc+ '/' + files_sort[i])
        #查看输入文件是否升序排列
        print(files_sort[i],flush=True)
    
    #定义一个保存所有文件中某一磁化分量的空列表
    m_allFiles = []
    for oneFileName in files_new:
        #按照文件顺序填充列表
        m_allFiles.append(fileload(oneFileName,column))
    
    return m_allFiles

#该函数的返回值为[array([...]), array([...])...]，列表的一个元素表示保存一个磁化文件的某个分量的浮点型数组
#列表长度为当前文件夹中所有子文件数量
#dirc：存放磁化文件的目录
#start_stage，end_stage：需要的磁化文件的范围
#exportX,exportY,exportZ：选择磁化矢量的那个分量表征斯格明子信息
#num：占用计算机核心的数量
def readUseMultiCore(dirc,start_stage,end_stage,exportX,exportY,exportZ,num):
    #磁化文件中的第三列表示Z分量
    if exportZ == 1:
        column = '2'
    #磁化文件中的第二列表示Y分量
    elif exportY == 1:
        column = '1'
    #磁化文件中的第一列表示X分量
    else:
        column = '0'

    #定义一个保存磁化文件名称的空列表
    files = []
    #walk函数会以文件夹为单位自顶而下遍历指定文件目录，
    #返回的三个参数分别表示当前文件夹, 当前文件夹中的子文件夹, 当前文件夹中的子文件
    for i,j,k in os.walk(dirc):
        #获取当前文件夹中所有磁化文件，并保存到列表中
        #因此，这里的files是二维列表：files[k[...]]
        files.append(k)
    #将files转化为一维列表
    files = files[0]
    #对列表中的磁化文件进行按名称升序排序
    files.sort()
    files_sort = files[:]
    #创建一个保存磁化文件全路径名称的列表
    files_new = []
    for i in range(start_stage,end_stage):
        files_new.append(dirc+ '/' + files_sort[i])
        #查看输入文件是否升序排列
        print(files_sort[i],flush=True)
    if num == 0:
        #没有指定核心数量时，表示使用所有cpu核心
        pool = Pool()
        #将需要扩展的的原始函数作为partial函数的第一个参数，原始函数的一系列参数作为partial的后续参数，最后生成一个带默认参数的新函数
        #接着pool.map会把新函数（第一个参数）和新函数的一系列参数（第二个参数即列表）映射到多进程池中运行
        #此处表示，返回读取所有磁化文件中的指定磁化分量的值
        m_allFiles = pool.map(partial(fileload,colum=column),files_new)
        #关闭进程池
        pool.close()
        #主进程阻塞等待子进程的退出，join方法要在close或terminate之后使用
        pool.join()
    else:
        pool = Pool(processes = num)
        m_allFiles = pool.map(partial(fileload,colum=column),files_new)
        pool.close()
        pool.join()
    
    return m_allFiles

2.筛选出每一个xy平面层中位于磁化分量阈值范围内的单元格

对于上文的返回结果列表m_allFiles而言，它的每一元素的数据类型为array([…])数组，存放着一个磁化文件中指定的数据列，即该磁化文件中所有单元格的指定磁化分量值，该数组中每一个元素的索引对应着OVF矢量场文件中单元格的分布顺序（先x，后y，最后z），通过这个对应关系可以根据数组中元素的索引来计算单元格的坐标：

"""
参考oommf命令行程序avf2odt的-defaultpos参数查看单元格坐标分布规律，根据x,y,z方向的单元格信息生成三个位置坐标列表，方便根据单元格的索引查表获取位置坐标
参数:
- x_start...z_cellSize: 磁化文件中单元格尺寸的信息

返回值: x_num,y_num,z_num: 磁体系在三个方向上的单元格总数
        cellPosition_x/y/z_list: 所有单元格的x/y/z坐标的索引列表
"""
def getCellPositionList(x_start,x_end,x_cellSize,y_start,y_end,y_cellSize,z_start,z_end,z_cellSize):
    #OVF矢量场格式保存单元格的顺序为：先x，后y，最后z，需要根据磁化文件中的行索引计算对应微磁模型中的3个空间坐标，并放入对应列表中
    x_cell_list = (np.arange(x_start,x_end,x_cellSize) + (x_cellSize / 2))
    y_cell_list = (np.arange(y_start,y_end,y_cellSize) + (y_cellSize / 2))
    z_cell_list = (np.arange(z_start,z_end,z_cellSize) + (z_cellSize / 2))
    x_num = len(x_cell_list)
    y_num = len(y_cell_list)
    z_num = len(z_cell_list)
    cellPosition_x_list,cellPosition_y_list,cellPosition_z_list = [],[],[]
    #3个列表的长度为微磁模型中单元格总数，遍历行索引，依次填充坐标列表
    for cell_index in range(0,int(x_num*y_num*z_num)):
        #根据索引计算单元格的x坐标索引
        x_index = int(cell_index % x_num)
        #根据索引计算单元格的y坐标索引
        y_index = int((cell_index / x_num) % y_num)
        #根据索引计算单元格的z坐标索引
        z_index = int((cell_index / (x_num * y_num)) % z_num)
        #根据坐标索引获取当前行（即单元格）的三个坐标，并放入对应列表
        cellPosition_x_list.append(x_cell_list[x_index])
        cellPosition_y_list.append(y_cell_list[y_index])
        cellPosition_z_list.append(z_cell_list[z_index])
    
    return x_num,y_num,z_num,cellPosition_x_list,cellPosition_y_list,cellPosition_z_list;

该函数会返回磁体系在三个方向上的单元格总数：x_num、y_num、z_num，以及单元格索引对应的三个坐标列表：cellPosition_x_list、cellPosition_y_list、cellPosition_z_list，比如OVF矢量场文件中磁体系大小为10X10X2 nm，单元格尺寸为1X1X1 nm，若我们想获取第101个单元格（从0开始）的位置坐标，只需使用上述的三个坐标列表及索引“101”，即可获取第101个单元格的位置坐标为(1.5nm,0.5nm,1.5nm)。
接着需要依次处理每一个磁化文件（即遍历列表m_allFiles），必须要考虑磁体系在z方向上有多层单元格的情况，这需要我们从下到上依次提取出每一个xy平面层中所有单元格，然后遍历每一个xy平面层中所有单元格，在排除掉无磁性的单元格之后，若剩余的某一单元格的磁化分量处于所我们设置的磁化分量阈值范围内(m_threshold_1 <= m <= m_threshold_2)，则认为该单元格位于当前xy平面层的畴壁中，否则位于磁畴中。我们需要排除位于磁畴区域的单元格，并将位于磁畴壁中的单元格放入一个列表mThrOneLayer_indexList，以供后面的识别斯格明子磁结构的三个方法使用。

"""
1.遍历每个磁化文件中的磁化分量数据，首先排除掉无磁性的单元格，接着在预设的磁化分量阈值内，按每一xy平面层依次识别出该层的所有磁结构
2.接着，从该xy平面层的所有磁结构中分类出斯格明子和其他畴壁类型
3.接着对该文件中的所有斯格明子进行处理：计算每个斯格明子的环状畴壁上的所有单元格的平均坐标作为中心，计算中心到环状畴壁的平均距离作为半径
参数:
- m_allFiles: 保存着所有磁化文件的某一磁化分量数据的列表
- m_threshold_1/2: 磁化强度分量的阈值(若单元格的磁化分量的值满足：m_threshold_1 <= m <= m_threshold_2，则认为该单元格位于畴壁中)，
通常单元格的磁化分量直接等于“0”表示是无磁性的，这是因为模拟结果中有磁性的单元格的磁化分量即便非常小，也不会直接等于“0”
- identifySkyMethod: 选择使用哪一种自定义方法识别斯格明子：1，自定义平均磁化方法，适用于磁体系中仅存在1个斯格明子磁结构；
2，自定义递归方法，适用于磁体系中存在多个斯格明子和（多个畴壁）；3，利用OpenCV库函数的方法，适用于磁体系中存在多个斯格明子和（多个畴壁）
- x_start...z_cellSize: 3个方向上的单元格尺寸信息

返回值: fileIndex_list: 读取并处理的磁化文件顺序
        allFilesSky_list: 按照文件读取顺序将每一个磁化文件中找到的斯格明子信息依次放入该结果列表，
其中每一个磁化文件中找到的斯格明子信息是一个用于存放多个矩阵（1行4列）的列表oneFilesSky_list，其中每个矩阵就表示一个斯格明子的信息，矩阵的4列分别表示斯格明子中心位置的x/y/z坐标和半径
"""
def getSkyInfo(m_allFiles,m_threshold_1,m_threshold_2,identifySkyMethod,
    x_start,x_end,x_cellSize,y_start,y_end,y_cellSize,z_start,z_end,z_cellSize):
    
    #根据x,y,z方向的单元格信息生成三个方向上的单元格数量，和三个位置坐标列表，方便根据单元格的索引查表获取位置坐标
    x_num,y_num,z_num,cellPosition_x_list,cellPosition_y_list,cellPosition_z_list = getCellPositionList(x_start,x_end,x_cellSize,y_start,y_end,y_cellSize,z_start,z_end,z_cellSize)

    #读取并处理的磁化文件顺序
    fileIndex_list = []
    #该函数返回的结果列表
    allFilesSky_list = []
    
    #遍历每一个磁化文件，找到每一个文件中处于阈值范围内的所有单元格
    for file_index in range(0,len(m_allFiles)):
        fileIndex_list.append(file_index)
        oneFile = m_allFiles[file_index]
        #定义1个保存单元格位置索引的列表，记录处于磁化分量阈值范围内的所有xy平面中的单元格
        mThrAllLayer_indexList = []
        for cell_index in range(0,len(oneFile)):
            if(oneFile[cell_index] == 0):
            #通常认为单元格的磁化分量直接等于“0”表示是无磁性的，这是因为模拟结果中有磁性的单元格的磁化分量即便非常小，也不会直接等于“0”
               continue;
            elif ((oneFile[cell_index] >= m_threshold_1) and (oneFile[cell_index] <= m_threshold_2)):
               mThrAllLayer_indexList.append(cell_index)
        print('在第 %d 个磁化文件中，磁化分量处于磁化分量阈值 m_threshold_1 ~ m_threshold_2 的单元格总数为：%d' % (file_index,len(mThrAllLayer_indexList)))
        print('开始使用自定义方法寻找当前磁化文件中的斯格明子信息')
        #定义一个保存当前磁化文件中所有斯格明子信息的列表
        oneFilesSky_list = []
        #首先计算磁体系在z方向的层数，即从下到上依次查找每一层xy平面中斯格明子信息
        allLayerNum = int((z_end - z_start) / z_cellSize)
        for layer_index in range(0,allLayerNum):
            #当前xy平面层的z坐标
            layerPosition_z = layer_index * z_cellSize + (z_cellSize / 2)
            #当前xy平面层中处于磁化分量阈值范围内的单元格
            mThrOneLayer_indexList = []
            for cell_index in mThrAllLayer_indexList:
                if cell_index >= (layer_index * x_num*y_num) and cell_index <= (layer_index+1) * x_num*y_num:
                   mThrOneLayer_indexList.append(cell_index)
                   #print(cellPosition_x_list[cell_index],cellPosition_y_list[cell_index],cellPosition_z_list[cell_index])
                else:
                   continue;
        
            if len(mThrOneLayer_indexList) < 1:
               #若当前xy平面层中没有处于磁化分量阈值范围内的单元格，则意味着当前层没有斯格明子
               #可以调节右边的数字，将由非常少的单元格组成的磁结构过滤掉
               continue;
            else:
               #定义一个保存当前xy平面层中所有斯格明子信息的列表
               oneLayerSky_list = []
               #使用自定义方法识别出当前磁化文件中的单个xy平面层中所有磁结构，这里提供三种方法：
               if identifySkyMethod == 1:
                  from identifySkyByCustomMethod import identifySkyBySimpleMethod
                  #第一种方法：适用于磁体系每一层的xy平面中仅存在一个斯格明子磁结构的情况
                  print('使用方法 1 查找第 %d 个文件，第 %d 层xy平面，仅存在一个斯格明子磁结构的情况'%(file_index,layer_index))
                  oneLayerSky_list = identifySkyBySimpleMethod(mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,layerPosition_z)
               elif identifySkyMethod == 2:
                  from identifySkyByCustomMethod import identifySkyByRecursiveMethod
                  #第二种方法：磁体系中每一层xy平面中存在多个斯格明子和（多个畴壁）
                  #考虑位于畴壁的一个单元格，它至少与畴壁上另一个单元格紧邻，即满足阈值距离，否则视为非畴壁中的单元格
                  #可以把阈值距离设置为np.sqrt(x_cellSize^2 + y_cellSize^2)，此处稍微增大一点为x_cellSize + y_cellSize
                  distance_thr = x_cellSize + y_cellSize
                  print('使用方法 2 查找第 %d 个文件，第 %d 层xy平面，存在多个斯格明子和（多个畴壁）的情况'%(file_index,layer_index))
                  oneLayerSky_list = identifySkyByRecursiveMethod(mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,layerPosition_z,distance_thr)

               else:
                  from identifySkyByOpenCVMethod import identifySkyByOpenCVMethod
                  print('使用方法 3 查找第 %d 个文件，第 %d 层xy平面，存在多个斯格明子和（多个畴壁）的情况'%(file_index,layer_index))
                  oneLayerSky_list = identifySkyByOpenCVMethod(mThrOneLayer_indexList,x_start,x_end,x_cellSize,y_start,y_end,y_cellSize,layerPosition_z)
               #将每一个xy平面层中所有斯格明子信息填充进当前磁化文件的斯格明子结果列表
               if len(oneLayerSky_list) > 0:
                  #注意此处使用extend而不是append函数来填充一个磁化文件的数据
                  oneFilesSky_list.extend(oneLayerSky_list)  
        #将每一个磁化文件中找到的斯格明子信息按照文件读取顺序填充进该函数返回的结果列表
        allFilesSky_list.append(oneFilesSky_list)

    return fileIndex_list,allFilesSky_list;

例如，在下图左面板所示的圆盘中仅存在一个斯格明子，采用磁化强度z分量的阈值范围为-200e-3~200e3，通过上述操作提取出了单个xy平面层中位于磁畴壁中的单元格，如右面板所示：

在这里插入图片描述

3.计算组成磁结构的所有单元格的平均坐标和平均距离

当单个xy平面层中仅存在一个斯格明子磁结构时，上文得到的结果列表mThrOneLayer_indexList中的单元格就是组成斯格明子的环状畴壁的单元格，所以无需进行额外操作，直接按照（一）中的思路，对这些处于磁化分量阈值范围内的所有单元格的坐标取平均值作为斯格明子的中心，并取该中心到这些单元格的平均距离为半径：

"""
适用于适用于磁体系每一xy平面层中仅存在一个斯格明子磁结构的情况：
计算斯格明子中心的方法：通常取位于环状畴壁的所有单元格的平均坐标作为中心，计算中心到环状畴壁的平均距离作为半径
参数:
- mThrOneLayer_indexList: 当前xy平面层中处于磁化分量阈值范围内的单元格位置索引列表
- cellPosition_x_list: 所有单元格的x坐标的索引列表
- cellPosition_y_list: 所有单元格的y坐标的索引列表
- layerPosition_z: 当前xy平面层的z坐标

返回值: skyrmion_list: 一个用于存放多个矩阵（1行4列）的列表，其中每个矩阵就表示一个斯格明子的信息，矩阵的4列分别表示斯格明子中心位置的x/y/z坐标和半径
"""
def identifySkyBySimpleMethod(mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,layerPosition_z):
    #定义该函数的结果列表
    skyrmion_list = []
    #定义当前xy平面层，位于磁化分量阈值范围内（斯格明子的环状畴壁）的所有单元格的2个位置坐标列表
    mThrPosition_x_list,mThrPosition_y_list = [],[]
    for index in mThrOneLayer_indexList:
        mThrPosition_x_list.append(cellPosition_x_list[index]) 
        mThrPosition_y_list.append(cellPosition_y_list[index])
    
    #取位于环状畴壁的所有单元格的平均坐标作为中心
    skyPosition_x = np.average(mThrPosition_x_list)
    skyPosition_y = np.average(mThrPosition_y_list)
    skyPosition_z = layerPosition_z
    #计算斯格明子中心到（环状）畴壁中所有单元格的平均距离作为半径
    skyPosition = np.array([skyPosition_x,skyPosition_y])
    #斯格明子中心到环状畴壁的所有单元格的总距离
    totalDistance = 0
    for circleDWCell_i in range(0,len(mThrOneLayer_indexList)):
        circleDWCell = np.array([mThrPosition_x_list[circleDWCell_i],mThrPosition_y_list[circleDWCell_i]])
        #计算两单元格的空间距离，并计入总距离
        totalDistance += np.linalg.norm(circleDWCell - skyPosition)
    skyRadius = totalDistance / len(mThrOneLayer_indexList)
    
    #填充矩阵，并将之放入要返回的结果列表
    skyrmion = np.array([skyPosition_x,skyPosition_y,skyPosition_z,skyRadius])
    skyrmion_list.append(skyrmion)
    return skyrmion_list;

在上述程序中使用斯格明子的位置坐标(x,y,z)和半径填充了一个1行4列的矩阵skyrmion，最后之所以不直接返回该矩阵而是将之填充到结果列表skyrmion_list中，是为了和后文两种方法的返回结果格式相同，方便进行后续统一处理。

三、当磁体系的单个xy平面层存在多个斯格明子和磁畴壁共存的情况

1.递归查找处于磁化分量阈值范围内的紧邻的单元格并分离成不重叠的磁结构

考虑下图左面板磁化文件中单个xy平面层包含一个斯格明子和一条形磁畴壁的情况，通过提取处于磁化分量阈值范围内的单元格如右面板所示：

在这里插入图片描述

首先我们需要对单个xy平面层中处于磁化分量阈值范围内的单元格进行处理：根据递归的方式查找紧邻的所有单元格，将找到的一系列紧邻单元格作为一个磁结构，并使用一个列表magTextureIndex_list记录每一个磁结构包含的所有单元格，如此处理磁化文件中每一个xy平面层，于是我们便分离出了所有不重叠的磁结构。此方法中单元格的“紧邻”距离阈值可以设置为两相邻单元格的最大距离，也可以稍微扩大为 distance_thr = x_cellSize + y_cellSize，只需注意不要让其超过两个磁结构的最小间隔距离即可：

"""
用于处理当前xy平面层中位于预设磁化分量阈值内的单元格的位置坐标，递归寻找组成磁结构的紧邻单元格
1.使用上述的递归函数，以指定的任一单元格为起始点，从满足磁化分量阈值的所有单元格中找到它的紧邻单元格，
如此，分离出了紧邻单元格构成的磁结构，适用于多个斯格明子，斯格明子和畴壁共存等情况
2.对于识别到的每一个磁结构，根据它们自身的单元格坐标排布规律来区分出斯格明子和畴壁
参数:
- mThrOneLayer_indexList: 当前xy平面层中处于磁化分量阈值范围内的单元格位置索引列表
- cellPosition_x_list: 所有单元格的x坐标的索引列表
- cellPosition_y_list: 所有单元格的y坐标的索引列表
- layerPosition_z: 当前xy平面层的z坐标

返回值: skyrmion_list: 一个用于存放多个矩阵（1行4列）的列表，其中每个矩阵就表示一个斯格明子的信息，矩阵的4列分别表示斯格明子中心位置的x/y/z坐标和半径
"""
def identifySkyByRecursiveMethod(mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,layerPosition_z,distance_thr):
    #定义该函数的结果列表
    skyrmion_list = []
    #定义一个计数列表保存每个磁结构包含的单元格数量
    magTextureIndex_list = []
    #定义已处理和未处理的单元格位置索引列表，每当识别到一个磁结构，就将其所有单元格索引放入haveFoundIndex_list
    haveFoundIndex_list = []
    noFoundIndex_list = mThrOneLayer_indexList[:]
    currentPoint_index = -1
    
    ##开始遍历处于磁化分量阈值中的所有单元格，分类单元格到各自的磁结构##
    #注意不要在遍历列表过程中修改列表内容！
    for currentPoint_index in mThrOneLayer_indexList:
        if currentPoint_index in haveFoundIndex_list:
           noFoundIndex_list.remove(currentPoint_index)
           continue;
        else:
            #调用递归函数，以currentPoint_index单元格为起始点，从满足磁化分量阈值的所有单元格中找到它的紧邻单元格
            neighborIndex_list = []
            recursiveNeighborCellByIndex(currentPoint_index,neighborIndex_list,mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,distance_thr)
            #记录已找到的单元格索引，即每个磁结构在haveFoundIndex_list中的起始索引和单元格数量
            magTextureIndex_list.append(len(neighborIndex_list))
            haveFoundIndex_list.extend(neighborIndex_list)
    ##结束遍历##
    
    #对每一个磁结构进行识别，判断该磁结构是斯格明子还是畴壁
    #记录已识别的所有磁结构中的所有单元格数量
    foundCellCount = 0
    for currentMagTexture_cellNum in magTextureIndex_list:
        #从顺序保存的所有磁结构的所有单元格列表中，根据每个磁结构包含的单元格数量来截取出各自的单元格索引列表
        magTexture_cell = haveFoundIndex_list[foundCellCount:(foundCellCount+currentMagTexture_cellNum)]
        foundCellCount += currentMagTexture_cellNum
        #定义每个磁结构中所有单元格的3个位置坐标列表
        texturePosition_x_list,texturePosition_y_list = [],[]
        for i in magTexture_cell:
            texturePosition_x_list.append(cellPosition_x_list[i])
            texturePosition_y_list.append(cellPosition_y_list[i])
        
        #####区分畴壁还是斯格明子？#####
        if isDWOrSkyrmion(texturePosition_x_list,texturePosition_y_list) == 0:
           #该磁结构是畴壁
           continue;
        else:
           #该磁结构是斯格明子
           #取位于环状畴壁的所有单元格的平均坐标作为中心
           skyPosition_x = np.average(texturePosition_x_list)
           skyPosition_y = np.average(texturePosition_y_list)
           skyPosition_z = layerPosition_z
           #计算斯格明子中心到（环状）畴壁中所有单元格的平均距离作为半径
           skyPosition = np.array([skyPosition_x,skyPosition_y])
           #计算斯格明子中心到环状畴壁的所有单元格的总距离
           totalDistance = 0
           for circleDWCell_i in range(0,currentMagTexture_cellNum):
               circleDWCell = np.array([texturePosition_x_list[circleDWCell_i],texturePosition_y_list[circleDWCell_i]])
               #计算两单元格的空间距离，并计入总距离
               totalDistance += np.linalg.norm(circleDWCell - skyPosition)
           skyRadius = totalDistance / currentMagTexture_cellNum
           #填充矩阵，并将之放入要返回的结果列表
           skyrmion = np.array([skyPosition_x,skyPosition_y,skyPosition_z,skyRadius])
           skyrmion_list.append(skyrmion)
    return skyrmion_list;

其中，关于如何递归查找一个磁结构中所有紧邻单元格的思路如下：假设存在一个初始列表为[1,2,5,7,3,4,11,9,8,12]，我们给定起点如8，这将从初始列表中找到下一个紧邻点（阈值为1）：7和9，接着从初始列表中去除已找到的紧邻点作为剩余列表[1,2,5,3,4,11,12]，然后将7作为起点，从剩余列表中没有找到紧邻点；然后将9作为起点，从剩余列表中没有找到紧邻点；如此递归查找，每找到一个紧邻点就将其放入结果列表中，最终，当再也没有紧邻点时，退出递归函数：

"""
计算xy平面内，指定单元格与列表中其余单元格的最小距离，当列表中只有一个单元格索引时，即计算两单元格的空间距离
参数:
- position_index: 起点单元格的索引
- position_index_list: 待比较的单元格索引列表
- excludeIndex_list: 从position_index_list中排除的单元格索引，即不与position_index比较距离的单元格列表
- cellPosition_x/y_list: 所有单元格的x/y坐标的索引列表

返回值: min_index,min_dist: 起点单元格与列表中最小距离的单元格索引及其距离
"""
def getMinDistanceByIndex(position_index,position_index_list,excludeIndex_list,cellPosition_x_list,cellPosition_y_list):
    #初始化最小距离为无穷大，索引为-1表示找不到距离最小值
    min_dist = float('inf')
    min_index = -1
    if position_index in position_index_list:
       print('getMinDistanceByIndex函数position_index索引与列表重复')
       min_dist = 0
    else:
        #获取指定单元格索引的位置坐标
        current_point = np.array([cellPosition_x_list[position_index],cellPosition_y_list[position_index]])
        for index in position_index_list:
            if index not in excludeIndex_list:
               next_point = np.array([cellPosition_x_list[index],cellPosition_y_list[index]])
               #计算两单元格的空间距离
               dist = np.linalg.norm(current_point - next_point)
               if dist < min_dist:
                   min_dist = dist
                   min_index = index
    return min_index,min_dist;

"""
定义一个递归函数，用于迭代寻找和起始单元格位置索引紧邻的其他单元格位置索引，它的迭代思路如下：
假设存在input_list=[1,2,5,7,3,4,11,9,8,12]：给定起点如8，寻找列表中下一个紧邻点（阈值为1），7和9，并分别将之作为起点，如此递归，
最后，output_list=[8, 7, 9]，即所需要的紧邻点列表
参数:
- start_index: 递归的起点单元格索引
- neighborIndex_list: 已找到的所有紧邻单元格的索引列表
- mThrOneLayer_indexList: 当前xy平面层中处于磁化分量阈值范围内的单元格位置索引列表
- cellPosition_x/y_list: 所有单元格的x/y/z坐标的索引列表
- distance_thr: 两格单元格满足紧邻关系的距离阈值

返回值: 无返回值，注意：从起点start_index开始的所有紧邻单元格存放在neighborIndex_list列表中
"""
def recursiveNeighborCellByIndex(start_index,neighborIndex_list,mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,distance_thr):
    #print('进入递归函数----start_index',start_index)
    #print('进入递归函数----neighborIndex_list',neighborIndex_list)
    #首先从所有单元格索引列表中排除已找到的紧邻单元格索引
    rem_mThrPosition_index_list = mThrOneLayer_indexList[:]
    #注意不要在遍历列表过程中修改列表内容！
    for index in mThrOneLayer_indexList:
        if index == start_index or index in neighborIndex_list:
           rem_mThrPosition_index_list.remove(index)
    #print('rem_mThrPosition_index_list',rem_mThrPosition_index_list)       
    #计算与当前单元格位置具有最小距离的单元格
    #把起点单元格作为第0个元素，视为紧邻单元格
    minNeighbor_list = [start_index]
    minNeighborCount = 1
    if start_index not in neighborIndex_list:
       neighborIndex_list.append(start_index)
    #以单元格start_index为起点，只寻找它的下一次递归时需要的所有紧邻单元格（不计算已找到的紧邻点）
    for index in mThrOneLayer_indexList:
        if index in neighborIndex_list:
           continue;
        else:
            min_index,min_dist = getMinDistanceByIndex(start_index,rem_mThrPosition_index_list,neighborIndex_list,cellPosition_x_list,cellPosition_y_list)
            if min_dist != 0 and min_dist <= distance_thr:
               minNeighborCount += 1
               neighborIndex_list.append(min_index)
               minNeighbor_list.append(min_index)
    #print('当前单元格的紧邻单元格列表：minNeighbor_list',minNeighbor_list)
    #print('初始起点单元格开始，所有递归的紧邻单元格列表neighborIndex_list',neighborIndex_list)
    #遍历以一个紧邻的单元格为起点，递归寻找它的紧邻单元格，minNeighborCount第0个元素是当前单元格，首先跳过它
    for i in range(1,minNeighborCount):
        #print('进入递归函数----')
        recursiveNeighborCellByIndex(minNeighbor_list[i],neighborIndex_list,mThrOneLayer_indexList,cellPosition_x_list,cellPosition_y_list,distance_thr)
        #print('退出递归函数----')
    return;

2.根据每一个磁结构的单元格排布规律来区分出斯格明子和磁畴壁

在每一个xy平面层中通过递归查找组成每一个磁结构的所有单元格之后，之后我们需要根据每一个磁结构的单元格排布规律来区分出斯格明子和磁畴壁。根据经验来看，一种大致可行的方法是：对比每一个磁结构在横纵方向的最大单元格差值，若差值过大，即该磁结构太“扁平”，则认为该磁结构是磁畴壁，否则将之识别为一个磁斯格明子：

"""
在xy平面层中，根据组成每一个磁结构的所有紧邻单元格的坐标信息，判断该磁结构是斯格明子还是畴壁
判断过程：分别计算水平和垂直方向上坐标的最大值与最小值之差：horizontal_Maxdiff和vertical_Maxdiff
若两者之间的差距超过距离阈值((horizontal_Maxdiff + vertical_Maxdiff) / 2 / 2)，即该磁结构非常“扁平”，则判定为畴壁，否则是斯格明子
参数:
- texturePosition_x/y_list: 组成一个磁结构的所有紧邻单元格的位置列表

返回值: 0: 该磁结构是畴壁
        1: 该磁结构是斯格明子
"""
def isDWOrSkyrmion(texturePosition_x_list,texturePosition_y_list):
    #分别计算水平和垂直方向上，坐标的最大值与最小值之差，作为评判依据
    horizontal_Maxdiff = np.max(texturePosition_x_list) - np.min(texturePosition_x_list)
    vertical_Maxdiff = np.max(texturePosition_y_list) - np.min(texturePosition_y_list)
    if abs(horizontal_Maxdiff - vertical_Maxdiff) >= ((horizontal_Maxdiff + vertical_Maxdiff) / 2 / 2):
       return 0;
    else:
       return 1;

当然，该方法可能并不靠谱，实际上一种较为准确的方法是判断每一个磁结构的单元格排布是否形成闭合，若闭合，则是斯格明子，否则是磁畴壁。当然，我并不知道该如何实现这个方法。。。

在这里插入图片描述

综上：处理多个斯格明子和磁畴壁共存的情况是稍微有点麻烦的，本小节的方法对处于磁化分量阈值范围内的所有单元格进行了递归，所以当这些单元格的数量达到上百个时，就会相当耗时，所以使用该方法时，我们需要综合考虑之后再设置一个最合适的最小磁化分量阈值范围，来筛选出位于畴壁区域的单元格，以此减少运行时间和提高识别准确性。

四、使用OpenCV库函数来识别“圆”特征

对于磁体系的每一个xy平面层，我们可以将每一个单元格映射到灰度图中的一个像素点，让处于磁化分量阈值范围内的单元格的像素值为白色，并让其余位于磁畴的单元格的像素值为黑色，然后就可以使用OpenCV的库函数cv2.HoughCircles来处理这个灰度图，最后提取出“圆”特征的中心位置和半径信息：

"""
使用OpenCV库中相关函数，识别每一xy平面层中任意数量的斯格明子，适用于任意磁体系：
1.对于磁体系的每一xy平面层，区分处于和不处于磁化分量阈值范围内的所有单元格，即畴壁区域和磁畴区域/非磁性区域的单元格，一个单元格对应一个像素，
注意磁体系的原点位于左下角，而图像矩阵的原点位于左上角，所以单元格映射为像素时需要转换y坐标，以此转化为灰度图
2.使用cv2.HoughCircles(image, method, dp, minDist, param1, param2, minRadius=0, maxRadius=0)函数检测灰度图中的类似圆的形状
参数:
- mThrOneLayer_indexList: 当前xy平面层中处于磁化分量阈值范围内的单元格位置索引列表
- x_start...y_cellSize: 磁化文件中单元格尺寸信息
- layerPosition_z: 当前xy平面层的z坐标
返回值: skyrmion_list: 一个用于存放多个矩阵（1行4列）的列表，其中每个矩阵就表示一个斯格明子的信息，矩阵的4列分别表示斯格明子中心位置的x/y坐标和半径
"""
def identifySkyByOpenCVMethod(mThrOneLayer_indexList,x_start,x_end,x_cellSize,y_start,y_end,y_cellSize,layerPosition_z):
    
    #定义该函数的结果列表
    skyrmion_list = []
    
    x_cell_list = (np.arange(x_start,x_end,x_cellSize) + (x_cellSize / 2))
    y_cell_list = (np.arange(y_start,y_end,y_cellSize) + (y_cellSize / 2))
    x_num = len(x_cell_list)
    y_num = len(y_cell_list)
    #一个单元格对应一个像素，以此将一层的单元格转化为一张灰度图
    height,width = y_num,x_num
    #创建一个灰度图映射矩阵：行(y)，列(x)
    grayImage_matrix = np.zeros((height, width), dtype=np.uint8)
    #根据已有的阈值内单元格索引mThrOneLayer_indexList映射到矩阵中的值设为白色像素值（255）
    #注意磁体系的原点位于左下角，而图像矩阵的原点位于左上角，所以单元格映射为像素时需要变换y坐标
    for cell_index in mThrOneLayer_indexList:
        #根据单元格索引解析出单元格的x坐标索引
        x_index = int(cell_index % x_num)
        #根据单元格索引解析出单元格的y坐标索引
        y_index = int((cell_index / x_num) % y_num)
        #转换y坐标
        y_index = y_num - y_index
        grayImage_matrix[y_index,x_index] = 255
    #进行图像预处理，高斯模糊，使用的是 5x5 大小的核，实现如降噪、平滑等效果，以便更好地检测圆环
    blurred = cv2.GaussianBlur(grayImage_matrix, (5, 5), 0)
    #绘制灰度图
    #cv2.imshow("blurred", blurred)
    #cv2.waitKey(0)
    #cv2.destroyAllWindows()
    #进行圆环检测
    circles = cv2.HoughCircles(blurred, cv2.HOUGH_GRADIENT, dp=1, minDist=10,
                        param1=50, param2=30, minRadius=2, maxRadius=0)

    if circles is not None:
       #将从图像中提取到的所有圆的浮点数进行四舍五入，将其转换为整数
       circles = np.round(circles).astype("int")
       for i in range(0,len(circles)):
           for (Fig_x,Fig_y,Fig_r) in circles[i]:
               #将图像中检测到的像素坐标转换到磁体系中对应的单元格
               skyPosition_x = x_cell_list[Fig_x]
               #注意变换y坐标
               skyPosition_y = y_cell_list[height - Fig_y]
               skyPosition_z = layerPosition_z
               skyRadius = Fig_r * (x_cellSize+y_cellSize)/2
               #填充矩阵，并将之放入要返回的结果列表
               skyrmion = np.array([skyPosition_x,skyPosition_y,skyPosition_z,skyRadius])
               skyrmion_list.append(skyrmion)
               #print("中心: ({},{},{}), 半径: {}".format(skyPosition_x,skyPosition_y,skyPosition_z,skyRadius))
    return skyrmion_list;

注意：磁体系的坐标系通常和图像的坐标系不一样，磁体系的坐标系通常位于左下角，而图像的坐标系位于左上角，所以当单元格和像素点相互映射时需要变换y坐标，这个问题在笔记04将一张图片映射为一个标量场时详细介绍过。该方法得到的灰度图如下所示：

在这里插入图片描述

综上：该方法需要识别灰度图中“圆”特征，所以需要位于斯格明子环状畴壁中的单元格越多越好，如此才能呈现出一个较好的“圆”，才能更准确的识别出灰度图中一个闭合的几何结构。

限于篇幅，关于后续如何保存每个磁化文件的斯格明子信息的代码非常简单，这里不再赘述，所以请直接查阅源程序了解。

五、测试验证

参考文献《Magnonic Frequency Comb through Nonlinear Magnon-Skyrmion Scattering》（DOI:10.1103/PhysRevLett.127.037202），我们尝试复现一下其补充材料的FIG.6，如下图所示：

在这里插入图片描述

首先，将该磁体系弛豫后，一个斯格明子会位于xy平面中心位置(500nm,500nm)，半径约为11nm左右，使用如下代码进行弛豫：

# MIF 2.1

#################
#author:YQYUN
#date:23/7/3
#desc:探究斯格明子位于xy平面中心，作为频率梳
#desc:1000*1000nm的平面，厚度1nm
#desc:初始磁化设置:在平面中心设置一个类斯格明子磁化分布
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

##########################划分模型的物理尺寸和单元格尺寸##########################

#xy平面尺寸：1000*1000*1nm
Parameter plane_length 1000
Parameter plane_width 1000
Parameter plane_height 1
set plane_length [expr {$plane_length * 1e-9}]
set plane_width [expr {$plane_width * 1e-9}]
set plane_height [expr {$plane_height * 1e-9}]

#容器的尺寸
set atlas_x $plane_length
set atlas_y $plane_width
set atlas_z $plane_height

#分配xy平面的区域
proc setRegions { x y z } {
	return 1
}


#定义容器
Specify Oxs_MultiAtlas:atlas [subst {
	comment "使用脚本函数定义模型"
	atlas { Oxs_ScriptAtlas {
		xrange { 0 $atlas_x }
		yrange { 0 $atlas_y }
		zrange { 0 $atlas_z }
		regions {planeRegion}
		script_args rawpt
		script setRegions
	}}
}]

#单元格尺寸：2*2*1nm
Parameter cellsize_x 2
Parameter cellsize_y 2
Parameter cellsize_z 1
set cellsize_x [expr {$cellsize_x * 1e-9}]
set cellsize_y [expr {$cellsize_y * 1e-9}]
set cellsize_z [expr {$cellsize_z * 1e-9}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$cellsize_x $cellsize_y $cellsize_z}
	atlas :atlas
}]

##########################划分模型的物理尺寸和单元格尺寸##########################

##########################指定材料的磁性参数和磁性能量##########################

#定义交换能（15pJ/m）
Parameter A 1.5e-11

Specify Oxs_UniformExchange [subst {
	A $A
}]

#定义单轴各向异性能（0.6MJ/m3）
Parameter K1 6e5

Specify Oxs_UniaxialAnisotropy [subst {
	K1 $K1
	axis {0 0 1}
}]

#定义退磁能
Specify Oxs_Demag {}

#定义界面DMI能（2.5mJ/m2，畴壁中面内磁矩由负指向正）
#若DMI符号相反（-2.5mJ/m2，畴壁中面内磁矩由正指向负）

Parameter plane_interDMI 2.5e-3

Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D 0
	atlas :atlas
	D {
	planeRegion planeRegion $plane_interDMI
	}
}]

#定义饱和磁化强度Ms（5.8e5A/m）
Parameter Ms 5.8e5

#定义一个标量场对象来设置不同区域的饱和磁化强度
Specify Oxs_AtlasScalarField:regions_Ms [subst {
	atlas :atlas
	comment "只有xy平面区域内有磁性，其他区域无磁性"
	default_value 0
	values {
	planeRegion $Ms
	}
}]

##########################指定材料的磁性参数和磁性能量##########################

##########################设置磁体系的初始磁化状态##########################

#分配xy平面内，中心区域的初始磁化分布为类似斯格明子的磁化分布，其他区域为+z分布
#斯格明子的中心和初始大小，即中心到畴壁外侧的外半径为：30nm，中心到畴壁内侧的内半径：15nm
set sky_core_x 500e-9
set sky_core_y 500e-9
set sky_outRadius 30e-9
set sky_inRadius 15e-9
#类斯格明子的内半径之内的区域的磁矩指向-z，内半径到外半径之间的面内磁矩指向圆外（需计算），外半径之外的磁矩指向+z
set sky_inRadiusMag "0 -0.1 -0.9"
set sky_outRadiusMag "0 0.1 0.9"
#其他磁性区域的磁矩指向+z
set otherMag "0 0 1"

proc setMagnetization { x y z } {
	global sky_core_x sky_core_y sky_outRadius sky_inRadius sky_inRadiusMag sky_outRadiusMag
	global otherMag
	
	#首先找到包围斯格明子的外接方形区域
	if {($x >= 470e-9 && $x <= 530e-9) && ($y >= 470e-9 && $y <= 530e-9)} {
	set tempRadius [expr {($x - $sky_core_x) * ($x - $sky_core_x) + ($y - $sky_core_y) * ($y - $sky_core_y)}]
	#接着在这个方形区域内找到内半径之内的区域
	if {$tempRadius <= $sky_inRadius * $sky_inRadius} {
	return $sky_inRadiusMag
	} elseif {$tempRadius <= $sky_outRadius * $sky_outRadius} {
	#接着是内半径和外半径之间的区域：磁化矢量方向为该点坐标减去中点坐标，即矢量背离中心
	set sky_planeMag_x [expr {$x - $sky_core_x}]
	set sky_planeMag_y [expr {$y - $sky_core_y}]
	set sky_planeMag_z 0
	return [list $sky_planeMag_x $sky_planeMag_y $sky_planeMag_z]
	} else {
	#最后找到外半径之外的区域
	return $sky_outRadiusMag
	}
	}
	#其余位置点的磁矩指向+z
	return $otherMag
}

#定义一个文件矢量场对象来设置不同区域的初始磁化
Specify Oxs_ScriptVectorField:regions_m0 {
	script setMagnetization
	script_args rawpt
	atlas :atlas
}

##########################设置磁体系的初始磁化状态##########################

##########################设置求解器和演化器##########################

#使用能量最小化演化器弛豫，保存磁化状态并作为后续模拟的基态
Specify Oxs_CGEvolve:evolver {}

#使用最小化驱动器快速推进到稳态
Specify Oxs_MinDriver [subst {
	evolver :evolver
	mesh :mesh
	stopping_mxHxm 0.01
	comment "设置饱和磁化强度"
	Ms :regions_Ms
	comment "设置初始磁化状态"
	m0 :regions_m0
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	comment "vector_field_output_format {text %#.17g}"
	comment "将checkpoint_interval设为10，每10分钟保存一次求解状态"
    checkpoint_interval 10
	checkpoint_disposal never
}]

##########################设置求解器和演化器##########################

##########################设置保存磁化文件相关##########################

Destination Record mmArchive
Schedule Oxs_MinDriver::Magnetization Record Done 1

##########################设置保存磁化文件相关##########################

弛豫结束后将保存的磁化文件重命令为“sky@center_relaxed.omf”，并将之作为后续动态模拟的基态，结果如下：

在这里插入图片描述

接着需要在xy平面的左端天线区域使用 $h_0sin(wt)\hat{x}$ 形式的微波外加磁场，其中 $h_0=150 mT$ ， $\frac{w}{2\pi}=80GHz$ ，由于文中并没有说明施加外加场的详细区域，这里暂且假设为x@50-60nm；文中也没有说明阻尼系数的详细设置，这里暂且设置为该薄膜四周0-10nm范围内为0.5、10-30nm范围内为0.1、其余范围内为0.001；模拟运行10ns，每间隔1.6ps保存一次磁化文件，，，综上，最终生成的代码如下：

# MIF 2.1

#################
#author:YQYUN
#date:23/7/3
#desc:探究斯格明子位于xy平面中心，在平面左端x:50-60nm范围内使用单频率激发场，查看斯格明子的响应
#desc:1000*1000nm的平面，厚度1nm
#desc:初始磁化设置:以弛豫后的基态磁化文件作为初始磁化，在平面中心存在一个斯格明子
#desc:在平面左端x:50-60nm范围内使用单频率激发场80GHz，119250A/m（150mT）的sin形式
#desc:直接将磁化文件保存为文本格式，方便用程序查看斯格明子信息
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

#使用时间驱动器的总共运行时间为10ns
Parameter run_time 10e-9
#每个阶段1.6ps
Parameter stage_time 1.6e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]


##########################划分模型的物理尺寸和单元格尺寸##########################

#xy平面尺寸：1000*1000*1nm
Parameter plane_length 1000
Parameter plane_width 1000
Parameter plane_height 1
set plane_length [expr {$plane_length * 1e-9}]
set plane_width [expr {$plane_width * 1e-9}]
set plane_height [expr {$plane_height * 1e-9}]

#容器的尺寸
set atlas_x $plane_length
set atlas_y $plane_width
set atlas_z $plane_height

#分配xy平面的区域
proc setRegions { x y z } {
	return 1
}


#定义容器
Specify Oxs_MultiAtlas:atlas [subst {
	comment "使用脚本函数定义模型"
	atlas { Oxs_ScriptAtlas {
		xrange { 0 $atlas_x }
		yrange { 0 $atlas_y }
		zrange { 0 $atlas_z }
		regions {planeRegion}
		script_args rawpt
		script setRegions
	}}
}]

#单元格尺寸：2*2*1nm
Parameter cellsize_x 2
Parameter cellsize_y 2
Parameter cellsize_z 1
set cellsize_x [expr {$cellsize_x * 1e-9}]
set cellsize_y [expr {$cellsize_y * 1e-9}]
set cellsize_z [expr {$cellsize_z * 1e-9}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$cellsize_x $cellsize_y $cellsize_z}
	atlas :atlas
}]

##########################划分模型的物理尺寸和单元格尺寸##########################

##########################指定材料的磁性参数和磁性能量##########################

#定义交换能（15pJ/m）
Parameter A 1.5e-11

Specify Oxs_UniformExchange [subst {
	A $A
}]

#定义单轴各向异性能（0.6MJ/m3）
Parameter K1 6e5

Specify Oxs_UniaxialAnisotropy [subst {
	K1 $K1
	axis {0 0 1}
}]

#定义退磁能
Specify Oxs_Demag {}

#定义界面DMI能（2.5mJ/m2，畴壁中面内磁矩由负指向正）
#若DMI符号相反（-2.5mJ/m2，畴壁中面内磁矩由正指向负）

Parameter plane_interDMI 2.5e-3

Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D 0
	atlas :atlas
	D {
	planeRegion planeRegion $plane_interDMI
	}
}]

#定义饱和磁化强度Ms（5.8e5A/m）
Parameter Ms 5.8e5

#定义一个标量场对象来设置不同区域的饱和磁化强度
Specify Oxs_AtlasScalarField:regions_Ms [subst {
	atlas :atlas
	comment "只有xy平面区域内有磁性，其他区域无磁性"
	default_value 0
	values {
	planeRegion $Ms
	}
}]

#定义阻尼系数
#xy平面四周 10nm 范围内为0.5
Parameter maxAlpha 0.5
Parameter maxAlphaRegion 10e-9
#xy平面四周 10-30nm范围内为0.1
Parameter middleAlpha 0.1
Parameter middleAlphaRegion 30e-9
#其余区域都为0.001
Parameter minAlpha 0.001

proc setAlpha { x y z } {
	global plane_length plane_width maxAlphaRegion middleAlphaRegion
	global maxAlpha middleAlpha minAlpha
	#分配左端的阻尼系数
	if {$x <= $middleAlphaRegion} {
	if {$x <= $maxAlphaRegion} {
	#xy平面左端10nm范围内
	return $maxAlpha
	} else {
	#左端10-30nm范围内
	return $middleAlpha
	}
	}
	#分配右端的阻尼系数
	if {$x >= $plane_length - $middleAlphaRegion} {
	if {$x >= $plane_length - $maxAlphaRegion} {
	#右端10nm范围内
	return $maxAlpha
	} else {
	#右端10-30nm范围内
	return $middleAlpha
	}
	}
	#分配xy平面下端的阻尼系数
	if {$y <= $middleAlphaRegion} {
	if {$y <= $maxAlphaRegion} {
	#xy平面下端10nm范围内
	return $maxAlpha
	} else {
	#下端10-30nm范围内
	return $middleAlpha
	}
	}
	#分配xy平面上端的阻尼系数
	if {$y >= $plane_width - $middleAlphaRegion} {
	if {$y >= $plane_width - $maxAlphaRegion} {
	#上端10nm范围内
	return $maxAlpha
	} else {
	#上端10-30nm范围内
	return $middleAlpha
	}
	}
	
	#分配中间区域的阻尼系数	
	return $minAlpha
}
#定义一个标量场对象来设置不同范围的阻尼系数
Specify Oxs_ScriptScalarField:regions_alpha { 
	script setAlpha
	script_args rawpt 
	atlas :atlas
}

##########################指定材料的磁性参数和磁性能量##########################

##########################设置磁体系的初始磁化状态##########################

#指定已经弛豫结束的基态磁化.omf文件名称
Parameter relaxedFileName "sky@center_relaxed.omf"
#定义一个文件矢量场对象来设置不同区域的初始磁化
Specify Oxs_FileVectorField:regions_m0 [subst {
    file $relaxedFileName
	atlas :atlas
}]

##########################设置磁体系的初始磁化状态##########################

##########################设置求解器和演化器##########################

#定义演化器（龙格-库塔时间演化器）
Specify Oxs_RungeKuttaEvolve:evolver [subst {
	comment "按照不同范围定义阻尼系数"
	alpha :regions_alpha
}]

#定义驱动器
Specify Oxs_TimeDriver [subst {
	evolver :evolver
	mesh :mesh
	comment "设置一个阶段的停止时间"
	stopping_time $stage_time
	comment "设置模拟包含的阶段数量"
	stage_count $number_of_stages
	comment "设置波导和调制器的饱和磁化强度"
	Ms :regions_Ms
	comment "设置初始磁化状态"
	m0 :regions_m0
	
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	vector_field_output_format {text %#.17g}
	
	comment "将checkpoint_interval设为10，每10分钟保存一次求解状态"
    checkpoint_interval 10
	checkpoint_disposal never
}]

##########################设置求解器和演化器##########################

##########################外加磁场相关设置##########################

#微波磁场的振幅，这里的单位为A/m
Parameter Happ 119250

#微波磁场的频率，这里的单位为GHz
Parameter frequency 80

#条带天线距离平面左端的距离
Parameter antennaOffset 50e-9
#条带天线的长度：整个平面长度范围
Parameter antennaLength 10e-9

#对初始的矢量场initialAntennaFiled进行变化，
#使其成为激发自旋波的外加磁场：Hx= Happ*sin(2*pi*frequency*t)
proc transformExcitationField { total_time } {
	global frequency pi
	set t $total_time
	#计算w=2*pi*f，并把单位顺便转化为GHz
	set w [expr {2 * $pi * $frequency * 1e9}]
	set sinwt [expr {sin($w * $t)}]
    set coswt [expr {cos($w * $t)}]
	#计算x方向的磁场分量及其对时间的导数
	#即x方向Hx*sinwt
	set Hx $sinwt
	set dHx [expr {$w * $coswt}]
	#其余两个方向都为0
	#返回6个元素的列表，即变换矩阵的3个主对角元素及其3个导数
	return [list $Hx 0 0 $dHx 0 0]
}

#指定天线区域的矢量场（后面转化为磁场）：H=($Happ 0 0)，其他区域H=(0 0 0)
proc initialAntennaField { x y z } {
    global Happ
	global antennaOffset antennaLength
	#天线距离波导左端 0nm,天线长度为 1000nm
	if {$x >= $antennaOffset && $x <= $antennaOffset + $antennaLength} {
	return "$Happ 0 0"
	}
	#其他区域无外加磁场
	return  "0 0 0"
}
#指定天线区域的矢量场
Specify Oxs_ScriptVectorField:antennaField {
	script initialAntennaField
	script_args rawpt
	atlas :atlas
}

#使用此类可生成任意（局域，时变）的外加磁场
Specify Oxs_TransformZeeman [subst {
    field :antennaField
	comment "函数返回6个元素，是3个主对角元素及其3个导数"
	type diagonal
	script transformExcitationField
	script_args total_time
	comment "默认单位A/m"
	comment "将stage_count设为0（默认值），让模拟的所有阶段都存在该塞曼能"
	stage_count 0
}]

##########################外加磁场相关设置##########################

##########################设置保存磁化文件相关##########################

Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1

##########################设置保存磁化文件相关##########################

模拟结束后，一共生成了6250个磁化文件，我们可以将这些磁化文件输出为图片然后拼接成一个视频，查看一下斯格明子的运动情况如下：

在平面左端使用h0@150mT，f@80GHz的sin场激发

这里使用方法一获取所有磁化文件中斯格明子的信息，该程序输出的图像如下所示：

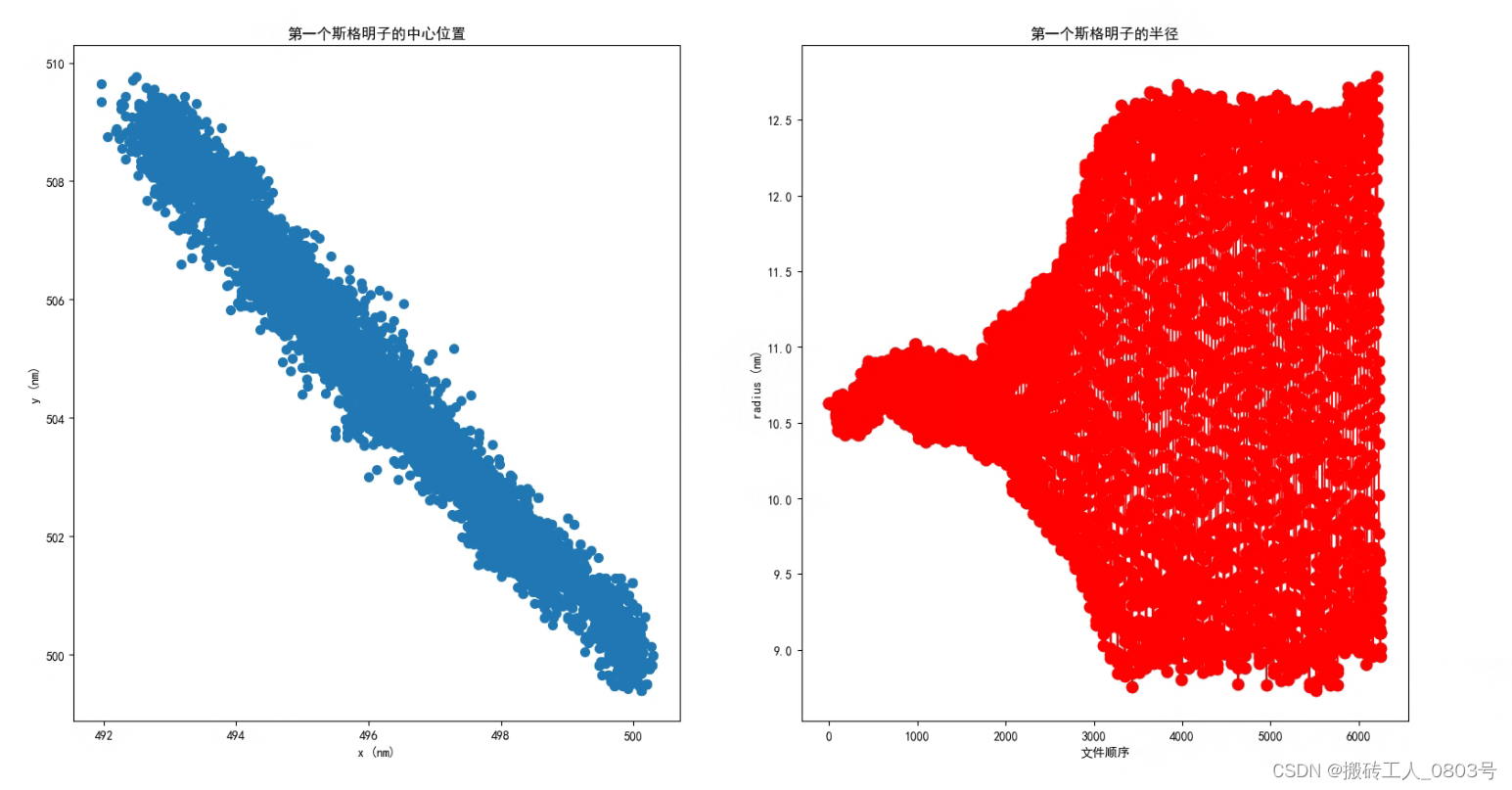
在这里插入图片描述

此外，该程序还会把从所有磁化文件中获取的所有斯格明子的信息按照文件读取顺序保存在一个文本文件“sky的位置和半径.txt”，该文件的第一列是文件顺序索引1,2,3，，，从第二列开始，每四列就是一个斯格明子的位置坐标(x,y,z)和半径，默认值-1表示无斯格明子信息。比如一个磁化文件中有两个斯格明子，在该行就有9列数据。接着还顺带利用笔记05中介绍过的MFA程序分析了包含斯格明子的区域内的频谱图，最终FIG.6的复现结果如下：

在这里插入图片描述

虽然与原图有着亿点差异，但基本的结论是相同的，可看到斯格明子确实往左上角运动，运动速度大约是0.85m/s，而且还伴随着呼吸模式，其半径在9-12nm范围内周期性变化。

总结

本文提供的获取每个磁化文件中斯格明子位置和半径的粗略方法仅供参考，最准确的方法毫无疑问是用肉眼直接观测，所以当用该程序得到结果之后，需要再用肉眼观测一些磁化文件进行检查验证。
该程序的源代码见下载链接，若大家觉得有错误或者需要优化改进的地方请在本文评论区留言。
最后，若觉得本文对大家有帮助的话麻烦来个一键三连吧。

在这里插入图片描述